Che nesso c’è tra la biologia e la matematica? Una prima risposta è stata presentata, nel primo atto, sul numero 12 di Emmeciquadro. Là l’autore ha messo a fuoco l’importanza dello strumento matematico nella comprensione di fenomeni biologici come la dinamica di popolazioni, l’evoluzione di un sistema ospite-parassita, la complessa fisiologia dei neuroni. Qui approfondisce il dibattito sull’utilità e applicabilità dei modelli matematici in biologia attraverso esempi relativi al livello molecolare: il protein folding, la TAC e il DNA computing.
L’autore ringrazia Giancarlo Travaglini per i commenti utili per la stesura finale del presente articolo.
Nella prima parte di questo articolo abbiamo introdotto il tema e accennato al caso dei sistemi dinamici. Abbiamo solo «sfiorato » alcuni argomenti mentre altri sono solo stati citati cercando di darne almeno una descrizione intuitiva. Per esempio abbiamo parlato di comportamento caotico senza darne una definizione formale ma solo una vaga idea sperando di avere comunque suscitato la curiosità del lettore.
Riprendiamo il racconto dal secondo atto, la scenografia è cambiata e si passa al livello molecolare; anche qualche attore in più fa la sua comparsa.
Atto II: il protein folding
Parleremo ora, in modo molto sintetico, di un problema estremamente importante, il protein folding: predire quale configurazione tridimensionale (e come viene raggiunta) verrà assunta da una proteina con una determinata struttura definita dalla sequenza di amminoacidi che la compongono.
Le proteine (prvtoz, primo) hanno un nome quanto mai appropriato: infatti, esse rappresentano, per così dire, la sostanza della vita. Sono presenti con funzione di sostegno in gran parte del corpo animale; si trovano come costituenti essenziali in tutte le cellule viventi, compongono la parte principale dei muscoli, della pelle, dei tendini, dei nervi e del sangue, formano gli enzimi, gli anticorpi e numerosi ormoni.
Potremmo suddividere le proteine in due categorie: proteine «di struttura» che servono come blocchi di base costitutivi degli organismi, proteine «funzionali» che intervengono come catalizzatori nei processi biochimici (per esempio enzimi).
Chimicamente le proteine sono dei grossi polimeri composti da una catena di amminoacidi uniti tra loro da legami peptidici. Ogni molecola di proteina contiene centinaia e anche migliaia di unità di amminoacidi e, dato che gli amminoacidi naturali sono venti, il numero delle diverse combinazioni è enorme. Le proteine si dividono in due grandi classi: le proteine fibrose (insolubili in acqua) e le proteine globulari (solubili in acqua o nelle soluzioni acquose di acidi, basi e sali).
Lo studio della costituzione delle proteine presenta diversi livelli: la struttura primaria, cioè la sequenza di amminoacidi, legati covalentemente con legami peptidici a formare la catena polipeptidica; la struttura secondaria, cioè l’organizzazione locale che può assumere la catena lineare di amminoacidi, mediante interazioni tra amminoacidi vicini tra loro (per esempio queste catene sono sistemate nello spazio formando spirali, lamine o sferoidi compatti); la struttura terziaria: la configurazione tridimensionale della catena polipeptidica che compone la proteina (risulta anche dalla interazione tra amminoacidi lontani nella sequenza lineare).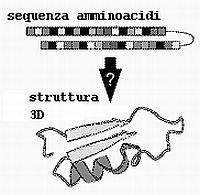 
Il problema del protein folding consiste, come abbiamo detto, nella predizione dell’architettura tridimensionale della proteina (struttura terziaria) partendo dalla catena lineare di amminoacidi. Nell’immagine a sinistra si mostra una schematizzazione grafica del problema.
Per certe proteine vi è anche la struttura quaternaria data dall’associazione di due o più catene polipeptidiche che concorrono a formare la molecola completa: di questo non ci occuperemo. Inoltre è stato dimostrato di recente che alcune grosse proteine, per potersi avvolgere e formare la struttura tridimensionale, hanno bisogno dell’aiuto di altre proteine, le chaperonine (dal francese chaperon).
Ma è importante conoscere la configurazione tridimensionale delle proteine? Non solo è importante ma essenziale per capire il funzionamento della proteina stessa.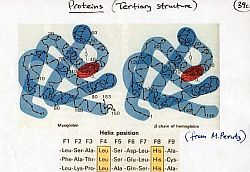 
Il premio Nobel 1962 per la chimica venne assegnato a M.F. Perutz e J.C. Kendrew dell’Università di Cambridge per la loro determinazione della struttura della emoglobina e della mioglobina, una molecola strettamente legata alla prima. [Immagine a destra: appunti di M.F. Perutz sulla struttura dell’emoglobina]
Usando la tecnica dei raggi X e conoscendo la sequenza degli amminoacidi, essi determinarono la forma tridimensionale di queste molecole estremamente complicate: in modo «più preciso» per la mioglobina e con buona approssimazione per l’emoglobina.
L’emoglobina è detta anche «la molecola che respira» e rende possibile il trasporto dell’ossigeno ai tessuti. Questa proteina cattura, in modo reversibile, l’ossigeno per trasportarlo dal polmone ai tessuti. Inversamente l’emoglobina permette il trasporto dell’anidride carbonica dai tessuti al polmone.
In un certo senso, con una immagine molto rozza, la proteina si apre, lega l’ossigeno, si richiude e viene trasportata. Senza la sua struttura tridimensionale non potrebbe svolgere tale compito di legame, trasporto e rilascio dell’ossigeno.
Clicca qui per accedere all’intero articolo in formato PDF
Vai alla prima parte dell’articolo pubblicato sul n° 12 di Emmeciquadro
Giovanni Naldi
(Professore Associato di Analisi Numerica presso il Dipartimento di Matematica e Applicazioni dell’Università degli Studi di Milano-Bicocca)
© Pubblicato sul n° 13 di Emmeciquadro
