Nella sua pur breve vita Riemann ha posto più di una pietra miliare nello sviluppo della matematica dell’Ottocento, di cui è uno dei principali protagonisti. Non è possibile, data la vastità della sua opera, darne un quadro completo nello spazio di un articolo; tuttavia questo contributo, oltre a ripercorrere la sua vicenda umana, indica le principale direzioni di ricerca: le geometrie non euclidee, l’analisi infinitesimale, la topologia, le applicazioni delle equazioni differenziali alla fisica. La sua opera costituisce una eredità ancor oggi feconda per la ricerca matematica e di fisica teorica.
A Verbania, in uno dei nove cimiteri della città, è sepolto un matematico tra i più originali dei tempi moderni: Bernhard Riemann. Una lapide in tedesco lo ricorda nel piccolo Camposanto di Selasca, frazione di Biganzolo, appena sopra Intra. La vita sofferente di questo rivoluzionario matematico si è chiusa infatti sulle rive del Lago Maggiore, dove aveva cercato sollievo alla sua precaria salute.
La vita
Georg Friedrich Bernhard Riemann nacque il 17 settembre del 1826 a Breselenz (Hannover) in Germania. Era il secondo di sei figli (due maschi e quattro femmine). Il padre Friedrich Bernhard, pastore luterano, aveva combattuto nelle guerre napoleoniche e, raggiunta la pace, sposò Charlotte Ebell, figlia di un consigliere di corte. Le condizioni di famiglia erano tutt’altro che prospere e dovette soffrire non poco: questo non gli impedì in seguito di ricordare con gioia la serenità di quei primi anni e di provare nostalgia quando si doveva allontanare dalla famiglia stessa.
Di carattere timido e schivo, aveva un sacro timore di esporsi e di parlare davanti a un uditorio. Questa timidezza gli creò anche negli anni successivi dei seri inconvenienti, specialmente quando doveva esporre in pubblico le sue geniali intuizioni nel campo della matematica. Ma a tale estrema riservatezza faceva contrasto una combattiva sicurezza basata sui suoi indiscutibili principi scientifici, frutto della sua creazione.
Ancora bambino, Riemann seguì il padre nella parrocchia di Quickborn ove era stato trasferito. Là ricevette dal padre stesso i primi rudimenti della sua istruzione e subito si dimostrò uno studente meraviglioso. I suoi primi interessi furono rivolti verso la storia, ma già a sei anni esplose il suo genio matematico. Non solo risolveva tutti i problemi che gli venivano sottoposti, ma inventava difficili rompicapo che esasperavano il fratello e le sorelle: era il primo segnale del suo genio creativo.
Raggiunti i dieci anni l’istruzione paterna non bastò più e fu affidato a un abile maestro di nome Schulz, il quale spesso ricevette insegnamenti dall’allievo più abile di lui a trovare soluzioni originali.
Gli anni del ginnasio
A quattordici anni Bernhard fu iscritto al Ginnasio di Hannover e andò ad alloggiare presso la nonna. Una volta di più il suo carattere lo portò all’isolamento e all’emarginazione. Solo, senza amici, si immerse nei suoi studi preferiti riportando risultati eccellenti: meravigliò i suoi compagni con alcune invenzioni, per esempio un originale calendario perpetuo, costruito con le sue mani per farne un regalo ai genitori.  Morta la nonna due anni dopo, Riemann si trasferì al Ginnasio di Luneburg che frequentò fino al termine dei suoi studi medi. Qui la scuola era vicino a casa, e ciò gli permetteva di passarvi molte ore della sua giornata. Furono gli anni più felici della sua vita. Si manifestò al ginnasio il suo perfezionismo che gli creò qualche difficoltà nei compiti scritti e che più tardi rallentò molto la sua produzione scientifica. Migliorò un po’ questo atteggiamento quando il suo professore di ebraico se lo prese in casa ove insieme si istruivano sui testi della Scrittura. Riemann infatti cercava di accontentare il padre che sognava per lui una brillante carriera di predicatore. Pur innamorato di tale carriera non giunse mai a eccellere, ma spese il suo talento matematico per cercare di dimostrare la verità della Genesi.
Morta la nonna due anni dopo, Riemann si trasferì al Ginnasio di Luneburg che frequentò fino al termine dei suoi studi medi. Qui la scuola era vicino a casa, e ciò gli permetteva di passarvi molte ore della sua giornata. Furono gli anni più felici della sua vita. Si manifestò al ginnasio il suo perfezionismo che gli creò qualche difficoltà nei compiti scritti e che più tardi rallentò molto la sua produzione scientifica. Migliorò un po’ questo atteggiamento quando il suo professore di ebraico se lo prese in casa ove insieme si istruivano sui testi della Scrittura. Riemann infatti cercava di accontentare il padre che sognava per lui una brillante carriera di predicatore. Pur innamorato di tale carriera non giunse mai a eccellere, ma spese il suo talento matematico per cercare di dimostrare la verità della Genesi.
Per nulla scoraggiato dell’insuccesso perseverò nella sua profonda fede di cristiano convinto per tutta la vita. Rispettò sempre le idee religiose degli altri, certo com’era che «in fatto di religione la cosa più importante è il quotidiano esame di coscienza» come scrive il matematico tedesco Julius Wilhelm Richard Dedekind (1831-1916). [Immagine sopra a sinistra]
Durante gli anni del ginnasio Riemann si innamorò di molte teorie nei vari campi della matematica: Leonhard Eulero (svizzero, 1707-1783), Carl Friedrick Gauss (tedesco, 1777-1855), Neils Henrik Abel (svedese, 1802-1829), Augustin Louis Cauchy (francese, 1789-1857) erano i suoi matematici preferiti.
Dalla facoltà di filosofia a quella di matematica
A diciannove anni si iscrisse alla facoltà di filosofia e teologia nella Universi¬tà di Göttingen. La scelta fu dettata dal desiderio di accontentare il padre, ma non gli impediva di seguire i corsi di Stern sulla teoria delle equazioni e degli integrali definiti, quelli di Gauss sulle equazioni binomie e quelli di Goldschmidt sul magnetismo terrestre.
La supplica rivolta al padre per cambiare facoltà fu finalmente esaudita e Riemann ne fu felice. Dopo un solo anno alla facoltà di matematica di Göttingen passò a Berlino ove per due anni fu alla scuola di Moritz Hermann von Jacobi (matematico tedesco, 1801-1874), Peter Gustav Dirichlet (matematico tedesco, 1805-1859), Jacob Steiner (matematico svizzero, 1796-1863) e Ferdinand Gotthold Max Eisenstein (matematico tedesco, 1823-1852). Dalla sua corrispondenza veniamo a sapere che in quegli anni si dedicò alla teoria dei numeri, agli integrali definiti, alla meccanica analitica, all’algebra superiore, alle funzioni di variabili complesse.  Durante la sollevazione del 1848 Riemann si arruolò nel corpo studentesco e gli capitò di dover proteggere il re nel suo palazzo, con turni di guardia di sedici ore. Nel 1849 ritornò a Göttingen per preparare il dottorato.
Durante la sollevazione del 1848 Riemann si arruolò nel corpo studentesco e gli capitò di dover proteggere il re nel suo palazzo, con turni di guardia di sedici ore. Nel 1849 ritornò a Göttingen per preparare il dottorato.
La fisica lo attirava quanto la matematica e vi dedicò molto tempo, tanto che seguì anche i corsi di fisica sperimentale tenuti da Wilhelm Eduard Weber (1804-1891), matematico tedesco del quale divenne grande amico. [Immagine a destra]
Ebbe anche il tempo di approfondire la filosofia e la biologia. I suoi studi di filosofia si indirizzarono soprattutto verso il filosofo tedesco Johann Friedrich Herbart: si formarono così i primi nuclei delle sue idee filosofiche come traspariranno poi dai suoi scritti. [Immagine che segue a sinistra: Johann F. Herbart (1776-1841)]
La dissertazione di dottorato
 L’amore della fisica gli fece tardare fino al 1851, all’età di venticinque anni, la dissertazione per il dottorato. Si trattava di un lavoro sui Fondamenti per una teoria generale delle funzioni a variabile complessa.
L’amore della fisica gli fece tardare fino al 1851, all’età di venticinque anni, la dissertazione per il dottorato. Si trattava di un lavoro sui Fondamenti per una teoria generale delle funzioni a variabile complessa.
Gauss confessò di aver avuto lui stesso da anni l’intenzione di trattare quell’argomento. Nel rapporto ufficiale, il maestro scrisse tra l’altro: «La dissertazione presentata dal Signor Riemann dà una convincente prova della capacità dell’autore, attraverso una penetrante indagine sui soggetti esposti, ed emerge una mente creativa, attiva e decisamente matematica, accompagnata da ori-ginalità fertile e meravigliosa. La presentazione è perspicace e concisa e a tratti bellissima. La maggior parte dei lettori avrebbe preferito maggior chiarezza di esposizione. L’insieme si presenta però come un lavoro so¬stanzioso e valido che non solo soddisfa le esigenze di un dottorato ma va molto al di là».  Il successo della discussione fu grande; soprattutto gli diede quella fiducia in sé che gli era sempre mancata. Scrisse al padre: «Credo di essere migliorato circa il concetto che ho di me, e spero anche di imparare a scrivere più velocemente e con maggior decisione, specialmente se dovrò inserirmi nelle società e fare lezioni e conferenze: mi sento incoraggiato». Si scusava poi col padre di non essersi presentato per il concorso di assistente all’Osservatorio di Göttingen, ma prometteva di «abilitarsi» come Privatdozent. Pensò quindi di preparare una memoria sulle serie di Fourier, e approfittò della presenza di Dirichlet a Göttingen per iniziare il lavoro. [Immagine a destra: Peter Gustav Dirichlet (1805-1859)]
Il successo della discussione fu grande; soprattutto gli diede quella fiducia in sé che gli era sempre mancata. Scrisse al padre: «Credo di essere migliorato circa il concetto che ho di me, e spero anche di imparare a scrivere più velocemente e con maggior decisione, specialmente se dovrò inserirmi nelle società e fare lezioni e conferenze: mi sento incoraggiato». Si scusava poi col padre di non essersi presentato per il concorso di assistente all’Osservatorio di Göttingen, ma prometteva di «abilitarsi» come Privatdozent. Pensò quindi di preparare una memoria sulle serie di Fourier, e approfittò della presenza di Dirichlet a Göttingen per iniziare il lavoro. [Immagine a destra: Peter Gustav Dirichlet (1805-1859)]
Nel dicembre del 1853, poté così consegnare il suo lavoro dal titolo Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe (Possibilità di rappresentare una funzione con una serie trigonometrica).
Ma la grande prova doveva avvenire con una pubblica discussione di fronte a una commissione di professori universitari.
Preparò tre argomenti per la prova di abilitazione sperando che i professori della facoltà scegliessero uno dei due su cui era particolarmente preparato. Ma Gauss che per sessant’anni aveva meditato sui fondamenti della geometria era curioso di vedere come quel «fertile genio» avrebbe affrontato tale soggetto e lo pregò di lavorarci sopra.
Riemann, che aveva solo ventisette anni, provò un certo smarrimento che comunicò al padre: «Mi trovo di nuovo in un grosso guaio: avendo ripreso le mie ricerche sui rapporti tra elettricità, magnetismo, luce e gravità ho raggiunto risultati tali da poterli pubblicare senza timori. Sono sempre più convinto che Gauss ha lavorato su tale argomento e ne ha discusso con alcuni amici (tra cui Weber). Te lo dico in confidenza, a costo di essere considerato presuntuoso, sono certo di non essere in ritardo e di poter essere considerato un ricercatore indipendente». [Immagine che segue a sinistra: Carl Friedrick Gauss (1777-1855)] Lo sforzo di condurre avanti contemporaneamente due difficili ricerche mentre lavorava come assistente di Weber nel seminario di fisica matematica, unite al solito problema della povertà, lo portò a un temporaneo esaurimento. Scrisse più tardi: «Fui talmente assorbito dalla mia ricerca sull’unità delle leggi fisiche che anche quando mi fu assegnato quell’argomento per la libera docenza non riuscii a strapparmi dalla mia ricerca. Così mi ammalai, in parte per l’eccesso di concentrazione e in parte per la continua permanenza in casa per colpa del brutto tempo; così ritornarono i miei vecchi disturbi. Solo dopo varie settimane mi sono sentito meglio, stimolato dal bel tempo e dai rapporti sociali. Durante l’estate ho preso in affitto una casa con giardino e così la salute non mi ha più dato fastidio. Due settimane dopo Pasqua, finito un lavoro urgente, ho preparato la mia dissertazione che ho terminato per Pentecoste, in sette settimane circa. Non so quando dovrò presentare questo lavoro perché Gauss è gravemente malato con poche speranze di guarigione. Essendo troppo debole mi ha chiesto di attendere fino ad agosto sperando di migliorare poiché sa bene che non vorrei aspettare fino al prossimo autunno. Pertanto il venerdì dopo Pentecoste decise per l’indomani alle 11.30. Così il sabato, tutto andò felicemente».
Lo sforzo di condurre avanti contemporaneamente due difficili ricerche mentre lavorava come assistente di Weber nel seminario di fisica matematica, unite al solito problema della povertà, lo portò a un temporaneo esaurimento. Scrisse più tardi: «Fui talmente assorbito dalla mia ricerca sull’unità delle leggi fisiche che anche quando mi fu assegnato quell’argomento per la libera docenza non riuscii a strapparmi dalla mia ricerca. Così mi ammalai, in parte per l’eccesso di concentrazione e in parte per la continua permanenza in casa per colpa del brutto tempo; così ritornarono i miei vecchi disturbi. Solo dopo varie settimane mi sono sentito meglio, stimolato dal bel tempo e dai rapporti sociali. Durante l’estate ho preso in affitto una casa con giardino e così la salute non mi ha più dato fastidio. Due settimane dopo Pasqua, finito un lavoro urgente, ho preparato la mia dissertazione che ho terminato per Pentecoste, in sette settimane circa. Non so quando dovrò presentare questo lavoro perché Gauss è gravemente malato con poche speranze di guarigione. Essendo troppo debole mi ha chiesto di attendere fino ad agosto sperando di migliorare poiché sa bene che non vorrei aspettare fino al prossimo autunno. Pertanto il venerdì dopo Pentecoste decise per l’indomani alle 11.30. Così il sabato, tutto andò felicemente».
Riemann racconta la presentazione di quella memorabile memoria che doveva rivoluzionare la geometria differenziale e preparare il cammino della fisica geometrica della nostra generazione: era il 10 giugno 1854. Egli aveva sudato sangue, ma ricevette un riconoscimento inaspettato.
Era nato un grande capolavoro della storia della matematica, rappresentato da quella memoria intitolata Über die Hypothesen, welche der Geometrie zu Grunde liegen. Gauss ne fu entusiasta.
Contro ogni tradizione aveva scelto il terzo soggetto proposto dal candidato, volendo vedere come se la sarebbe cavata quel giovane studente. Rimase sorpreso oltre ogni aspettativa e tornando dalla riunione volle manifestare a Weber il suo incondizionato apprezzamento circa le idee sostenute da Riemann esprimendosi con un calore che gli era inconsueto.
Gli studi di fisica
Per conto proprio Riemann continuava gli studi di fisica. Lo rileviamo da non poche lettere ai familiari. Ecco quanto scrive al fratello Wilhelm il 28 dicembre 1853. «Le cose vanno abbastanza bene relativamente ai miei lavori, ho consegnato ai primi di dicembre il mio scritto per l’abilitazione. L’altra mia ricerca sulla relazione tra elettricità, galvanismo luce e peso l’ho presa immediatamente dopo aver terminato la mia abilitazione, e ho esteso tanto il lavoro da non poterlo pubblicare cosi com’è. Ma mi sono reso conto che Gauss ci lavora da parecchi anni come mi hanno comunicato in segreto alcuni amici. Senza voler essere presuntuoso, ti posso dire che si dovrà riconoscere che queste cose le ho scoperte da solo».
 Tentò le prime spiegazioni del fenomeno dei condensatori e in particolare sulla capacità elettrica della bottiglia di Leida. Ancora in questa sua lunga lettera al fratello aggiunge: «Parlai con Kohlrausch delle mie scoperte sulle relazioni esistenti tra elettricità, luce e magnetismo, e gli ho passato l’elaborato. Kohlrausch mi ha risposto molto gentilmente, e mi ha offerto di spedire il mio lavoro a Berlino perché venga stampato da Poggendorf, stampatore degli Annali di Fisica e Chimica». [Immagine a destra: Friedrich Wilhelm Georg Kohlrausch (1840-1910)]
Tentò le prime spiegazioni del fenomeno dei condensatori e in particolare sulla capacità elettrica della bottiglia di Leida. Ancora in questa sua lunga lettera al fratello aggiunge: «Parlai con Kohlrausch delle mie scoperte sulle relazioni esistenti tra elettricità, luce e magnetismo, e gli ho passato l’elaborato. Kohlrausch mi ha risposto molto gentilmente, e mi ha offerto di spedire il mio lavoro a Berlino perché venga stampato da Poggendorf, stampatore degli Annali di Fisica e Chimica». [Immagine a destra: Friedrich Wilhelm Georg Kohlrausch (1840-1910)]
Nel settembre del 1854 Riemann partecipò a Göttingen al convegno dei naturalisti. Weber e Stern lo convinsero a tenere una relazione nella sezione fisico-matematica sull’elettrizzazione degli isolanti. Scrisse al padre in quella circostanza: «Dovevo tenere la mia relazione giovedì, ma dato che il mio era l’unico intervento nella nostra sezione, l’ho elaborato ancora la sera precedente per riuscire a riempire tutto il tempo messo a mia disposizione. All’inizio avevo soltanto accennato alla legge che volevo esporre, ma poi aggiunsi numerose manifestazioni di questa e dimostrai la concordanza di queste con l’esperienza. Ho parlato per un’ora e un quarto».  Decise in seguito di non pubblicare la memoria sulla capacità dei condensatori, ma in compenso pubblicò uno studio sulla teoria degli anelli ottici del matematico italiano Leopoldo Nobili. [Immagine a sinistra: Leopoldo Nobili (1787-1910). Incisione L. Ducci & C., 1843]
Decise in seguito di non pubblicare la memoria sulla capacità dei condensatori, ma in compenso pubblicò uno studio sulla teoria degli anelli ottici del matematico italiano Leopoldo Nobili. [Immagine a sinistra: Leopoldo Nobili (1787-1910). Incisione L. Ducci & C., 1843]
In una lettera alla sorella Ida descrive con entusiasmo la sua prima lezione sulla teoria delle equazioni differenziali parziali applicata a problemi fisici.
Nel 1855 Dirichlet succedette a Gauss (morto il 23 febbraio di quell’anno) e gli amici di Riemann si adoperarono perché ne divenisse l’assistente; ma le finanze dell’Università non lo permettevano. Gli fu comunque conces¬so uno stipendio (200 soldi l’anno) che era un po’ più elevato dell’incerto guadagno che ricavava dai pochi studenti che seguivano un suo corso facoltativo. Lo preoccupava il futuro. Quando perse il padre e la sorella Clara, divenne impossibile per lui passare le vacanze a Quickborn e si sentì povero e abbandonato. Le altre tre sorelle andarono a vivere con l’altro fratello, impiegato alle poste di Brema, il cui stipendio era principesco rispetto a quello del matematico.
Un esaurimento nervoso costrinse Riemann nel 1857 a interrompere il lavoro e prendersi un po’ di riposo sulle montagna dell’Hartz con Dedekind (suo primo biografo per volere di Weber) e un altro amico. Si divertirono a camminare e anche a giocare coi numeri o con le leggi fisiche criticando benevolmente i grandi della scienza passata per certe affermazioni… ridicole (per esempio Newton per la teoria delle azioni a distanza).
La cattedra all’Università
Nominato assistente all’Università, Riemann poteva finalmente ritenersi tranquillo dal punto di vista economico, ma la morte del fratello Wilhelm lo obbligò a prendersi cura delle tre sorelle, ciò che lo obbligò a raddop¬piare fatiche e privazioni. Alla morte di Dirichlet, Riemann fu nominato suo successore: aveva 33 anni. I riconoscimenti nazionali e internazionali (specialmente dalla Royal Society of London e dall’Académie Française des Sciences) fioccarono da ogni parte.  Raggiunto un certo benessere pensò di prendere moglie. Si sposò il 3 giugno del 1862 con Elise Koch, amica delle sue sorelle. Ma nel luglio dello stesso anno si ammalò di pleurite che degenerò in tubercolosi. Il governo gli passò un sussidio che l’aiutò a trascorrere l’inverno in Italia, dalla Sicilia a Napoli, a Roma, a Genova.
Raggiunto un certo benessere pensò di prendere moglie. Si sposò il 3 giugno del 1862 con Elise Koch, amica delle sue sorelle. Ma nel luglio dello stesso anno si ammalò di pleurite che degenerò in tubercolosi. Il governo gli passò un sussidio che l’aiutò a trascorrere l’inverno in Italia, dalla Sicilia a Napoli, a Roma, a Genova.
Rientrò in Germania nella primavera successiva felice delle nuove conoscenze che l’arte italiana gli aveva offerto. Era pieno di speranza, ma la malattia scoppiò più violenta appena giunto a Göttingen. Già allo Spluga si era preso un potente raffreddore.
Tornò in Italia nell’agosto del 1863 e soggiornò a Pisa dove nacque sua figlia Ida. L’inverno fu particolarmente rigido tanto che l’Arno ghiacciò e la sua più giovane sorella, Helene, morì. I matematici italiani gli dimostrarono stima e amicizia.  I professori Enrico Betti ed Eugenio Beltrami si ispirarono alle sue idee per portare importanti contributi alla topologia e alla geometria differenziale. [Immagine sopra a destra: Eugenio Beltrami (1835-1900)]
I professori Enrico Betti ed Eugenio Beltrami si ispirarono alle sue idee per portare importanti contributi alla topologia e alla geometria differenziale. [Immagine sopra a destra: Eugenio Beltrami (1835-1900)]
Beltrami vide come il concetto di spazio curvo di Riemann poteva serviredi base a una geometria non euclidea, scoperta certamente rivoluzionaria che condusse molto più lontano di quanto forse Riemann stesso non avesse previsto.
Ebbe anche scambi di idee con altri matematici italiani: Francesco Brioschi, professore di Analisi a Pisa e fondatore del Politecnico di Milano e Felice Casorati che contribuì a introdurre in Italia le nuove concezioni di Riemann. [Immagine qui a sinistra: Francesco Brioschi (1824-1897)]
L’Università di Pisa gli offrì la cattedra di Matematica, ma egli dovette rifiutare con rammarico, anche se l’Università di Göttingen gli aveva prolungato il tempo di permanenza lontano dall’insegnamento.
I problemi di salute e la morte
La salute non migliorò; anzi le cose si complicarono. A nulla valsero i soggiorni a Livorno e a Genova e decise di rientrare a casa. Là riprese il lavoro nei momenti in cui le forze lo reggevano.
Dedekind scrive: «I viaggi che Riemann fece in Italia nonostante il triste motivo che li causarono, costituirono per lui un momento affascinante: non solo per lo splendore del Paese, della natura, dell’arte, eccetera, che gli procurarono felicità, ma per la grande libertà di cui ha potuto godere, senza le costrizioni degli orari di insegnamento. In aggiunta al benefico effetto del clima, tutto questo contribuì a migliorare notevolmente il suo stato di salute». [Immagine qui a destra: Entico Betti (1823-1892)] – [Immagine che segue a sinistra: Felice Casorati (1835-1890)] In un estremo desiderio di guarire, nel giugno del 1866 tornò in Italia, sul lago Maggiore: era il suo terzo viaggio in Italia.
In un estremo desiderio di guarire, nel giugno del 1866 tornò in Italia, sul lago Maggiore: era il suo terzo viaggio in Italia.  Dimorò per qualche tempo nel Comune di Arizzano, sopra Intra, con la moglie Elise, ospiti di amici tedeschi.
Dimorò per qualche tempo nel Comune di Arizzano, sopra Intra, con la moglie Elise, ospiti di amici tedeschi.
Il 19 luglio di quello stesso anno scese a Biganzolo-Selasca (sempre nel Comune di Arizzano, poi Comune di Intra e ora di Verbania), in una villa presa in affitto.
Si tratta della Villa Pisoni successivamente acquistata e ricostruita dalla famiglia Zust. Ma il mattino del giorno seguente alle ore otto cessò di vivere.
Dedekind così descrive la morte dell’amico: «Le forze si affievolivano rapidamente: sentiva che la sua fine era prossima. Il giorno prima di morire lavorò sotto una pianta di fico, felice, dinnanzi al meraviglioso paesaggio che lo circondava […] La sua vita declinava gradualmente senza lotta e senza agonia mortale; sembrava che egli seguisse con interesse la separazione dell’anima dal corpo. Mentre sua moglie gli porgeva pane e vino, le disse: “bacia la nostra bimba”. Essa tenendogli le mani tra le sue ripeté per lui il Padre Nostro quando non fu più in grado di parlare. Alle parole “perdona i nostri debiti” volse lo sguardo in alto con devozione; essa sentì le mani di lui diventare fredde e dopo qualche sospiro il suo nobile e ardente cuore cessò di battere. Quell’anima nata candida nella casa di suo padre, si mantenne tale tutta la vita e servì fedelmente il suo Dio come fece suo padre, anche se in modo diverso».  Così è morto Bernhard Riemann nel massimo dello splendore del suo genio il 20 luglio 1866, non ancora quarantenne. In quei giorni stava lavorando sulle diverse fasi della filosofia naturale a partire dal tentativo di unificare la teoria della gravità e della luce, fino alla teoria della meccanica dell’orecchio umano.
Così è morto Bernhard Riemann nel massimo dello splendore del suo genio il 20 luglio 1866, non ancora quarantenne. In quei giorni stava lavorando sulle diverse fasi della filosofia naturale a partire dal tentativo di unificare la teoria della gravità e della luce, fino alla teoria della meccanica dell’orecchio umano.
La sua morte non fu allora avvertita dal mondo scientifico: Selasca era lontana dai grandi centri culturali; Riemann poi era tedesco e per di più protestante. Il fatto di non essere cattolico creò subito il problema del luogo della sepoltura: quel piccolo cimitero era riservato ai soli cattolici, ed egli avrebbe dovuto essere sepolto altrove, in una particolare area del cimitero che fosse riservata ai non cattolici. Ma prevalse il buon senso e la carità cristiana; deceduto a poche centinaia di metri dal Camposanto di Biganzolo-Selasca, là doveva essere sepolto. Tanto più che si trattava di un cristiano di una onestà unica e molto osservante delle sue pratiche religiose. E così colà riposa.
I suoi resti mortali sono ormai passati nella fossa comune. Resta solo la lapide , murata nelle vicinanze del cancello d’entrata del Cimitero di Selasca, fatta erigere dai suoi amici italiani. Il luogo è meta di «pellegrinaggio» di studiosi – più tedeschi che italiani – che intendono onorare il grande matematico. [Immagine sopra a destra: la lapide posta sulla tomba di Riemann con l’iscrizione in tedesco che traduce il latino della sacra Scrittura: Diligentibus Deum omnia cooperatur in bonum (Rom. 8,28)]
La vastità dell’opera di Riemann |
Riemann e la geometria non euclidea
Non intendiamo qui addentrarci nell’affascinante campo delle geometrie non euclidee, né tracciare la storia delle successive tappe delle nuove geometrie con i loro ricchi contributi alle varie branche delle scienze.
Solo ci interessa sottolineare in tale processo l’importanza fondamentale del nostro Riemann. Fin dal 1816 Gauss si interessò alla geometria differenziale, e pubblicò nel 1827 il suo definitivo pensiero sull’argomento in una memoria intitolata: Disquisitiones generales circa superficies curvas.
Un concetto nuovo e molto stimolante, ivi espresso, afferma che «una superficie è uno spazio in sé». Riemann colse tale idea e la generalizzò, tanto che sotto la sua spinta le geometrie non euclidee furono fatte rientrare come casi particolari nell’immenso complesso delle geometrie riemanniane. Si aprirono così nuove vedute sulle geometrie non euclidee.
L’inizio delle geometrie non euclidee
Fin dai tempi più antichi il V postulato di Euclide richiamò l’attenzione dei geometri perché non sembrava tanto evidente. Ne furono perciò tentate diverse dimostrazioni.  Ma tutte richiedevano l’introduzione di altri postulati che in definitiva venivano a sostituirsi al postulato euclideo. Il matematico italiano Giovanni Gerolamo Saccheri, S.J. (1667-1733) tentò una dimostrazione della verità di tale postulato nell’opera Euclídes ab omni naevo vindicatus. Ma, ironia della sorte, tale studio va riguardato come la prima opera di geometria non euclidea.
Ma tutte richiedevano l’introduzione di altri postulati che in definitiva venivano a sostituirsi al postulato euclideo. Il matematico italiano Giovanni Gerolamo Saccheri, S.J. (1667-1733) tentò una dimostrazione della verità di tale postulato nell’opera Euclídes ab omni naevo vindicatus. Ma, ironia della sorte, tale studio va riguardato come la prima opera di geometria non euclidea.
Più tardi però gli studiosi di geometria cominciarono a dubitare della verità assoluta del postulato di Euclide e si convinsero pertanto che sono ammissibili altre geometrie che non accettino o che addirittura neghino tale postulato. Questo accadde soprattutto quando vennero alla luce le opere del matematico russo Nicola Lobačevsky e del matematico ungherese Janos Bolyai. [Immagine qui a sinistra: Nikolaj Ivanovič Lobačevsky (1793-18565)] Quest’ultimo continuò le ricerche del padre Farkas (1775-1856) anche quando ne fu scoraggiato dal padre stesso che gli scrisse: «Per l’amor di Dio smettila di approfondire la cosa. Rifuggila non meno delle passioni sensuali, poiché anche questa può portare via tutto il tuo tempo e privarti della salute, della pace interiore, e della felicità nella vita». [Immagine a destra: Janos Bolyai (1802-1860)]
Quest’ultimo continuò le ricerche del padre Farkas (1775-1856) anche quando ne fu scoraggiato dal padre stesso che gli scrisse: «Per l’amor di Dio smettila di approfondire la cosa. Rifuggila non meno delle passioni sensuali, poiché anche questa può portare via tutto il tuo tempo e privarti della salute, della pace interiore, e della felicità nella vita». [Immagine a destra: Janos Bolyai (1802-1860)]
Quando Bolyai padre scrisse a Gauss per conoscere la sua opinione sull’opera eterodossa del proprio figlio, ricevette una risposta curiosa: non lo poteva lodare perché avrebbe significato una lode per se stesso, visto che quelle medesime vedute erano sue da anni. II povero Janos Bolyai ne fu molto dispiaciuto, temendo di perdere la priorità della scoperta. E fu ancora più sconvolto dal fatto che fosse stato pubblicato in Germania nel 1840 lo studio di Lobacevsky sull’argomento, tanto che decise di non pubblicare altro sulle sue idee di geometria non euclidea.
Da quel momento molti altri matematici si cimentarono intorno alle geometrie non euclidee. Le scoperte si fecero strada fra molti dubbi, errori e malintesi. Sembrava una pazzia.
|
La indimostrabilità del Quinto Postulato Si lavorò molto nel tentativo di provare il V postulato di Euclide, ma solo nel XX secolo si giunse a dimostrarne la indimostrabilità. E cioè venne provato che tale postulato non consegue dalle precedenti proposizioni del primo libro degli Elementi.  Questo significa che una geometria fondata sui quattro precedenti postulati non presenta alcuna contraddizione logica. Adrien-Marie Legendre stabilì una Geometria che prescinde dal V Postulato (Eléments de Géométrie del 1794) in una rielaborazione degli Elementi di Euclide, ove espone alcuni teoremi già intuiti dal Saccheri. Non potendo andare oltre in questa storia, ci limitiamo a citare una frase pronunciata da Jean-Baptiste D’Alembert (francese, 1717-1783) nel 1759, da cui possiamo intuire la portata polemica della ricerca a questo soggetto: «La définition et les propriétés de la ligne droite, ainsi que des lignes paralleles, sont l’écueil et le scandal des éléments de géométrie.» (Citato da Federigo Enriques in Le matematiche nella storia della cultura, Bologna 1938). [Immagine a sinistra: Federigo Enriques (1882-1946)] Questo significa che una geometria fondata sui quattro precedenti postulati non presenta alcuna contraddizione logica. Adrien-Marie Legendre stabilì una Geometria che prescinde dal V Postulato (Eléments de Géométrie del 1794) in una rielaborazione degli Elementi di Euclide, ove espone alcuni teoremi già intuiti dal Saccheri. Non potendo andare oltre in questa storia, ci limitiamo a citare una frase pronunciata da Jean-Baptiste D’Alembert (francese, 1717-1783) nel 1759, da cui possiamo intuire la portata polemica della ricerca a questo soggetto: «La définition et les propriétés de la ligne droite, ainsi que des lignes paralleles, sont l’écueil et le scandal des éléments de géométrie.» (Citato da Federigo Enriques in Le matematiche nella storia della cultura, Bologna 1938). [Immagine a sinistra: Federigo Enriques (1882-1946)]  Prima ancora dei matematici del Settecento, Euclide visse il dramma di questo postulato: lui che tante pur difficili e sottili dimostrazioni aveva escogitato, non riuscì a dimostrare una così semplice proposizione che egli pur riteneva essere vera; e la enuncia come postulato. Attilio Frajese nel suo libro Attraverso la storia della matematica (Le Monnier, 1969) così si esprime: «Nell’enunciare il quinto postulato, Euclide commise un atto di umiltà: riconobbe infatti l’insuccesso dei suoi tentativi di dimostrazione, e rinunciò a ogni tentativo ulteriore, dandosi per vinto. Ma commise al tempo stesso un atto di orgoglio: “Io, Euclide, – ha l’aria di dire – non ho saputo trovare la dimostrazione, ma neppure i miei posteri sapranno trovarla: perciò codifico in modo definitivo come postulato questa proposizione.” E i posteri gli hanno dato ragione.» [Immagine a destra: Attilio Frajese (1902-1986)] Prima ancora dei matematici del Settecento, Euclide visse il dramma di questo postulato: lui che tante pur difficili e sottili dimostrazioni aveva escogitato, non riuscì a dimostrare una così semplice proposizione che egli pur riteneva essere vera; e la enuncia come postulato. Attilio Frajese nel suo libro Attraverso la storia della matematica (Le Monnier, 1969) così si esprime: «Nell’enunciare il quinto postulato, Euclide commise un atto di umiltà: riconobbe infatti l’insuccesso dei suoi tentativi di dimostrazione, e rinunciò a ogni tentativo ulteriore, dandosi per vinto. Ma commise al tempo stesso un atto di orgoglio: “Io, Euclide, – ha l’aria di dire – non ho saputo trovare la dimostrazione, ma neppure i miei posteri sapranno trovarla: perciò codifico in modo definitivo come postulato questa proposizione.” E i posteri gli hanno dato ragione.» [Immagine a destra: Attilio Frajese (1902-1986)]All’inizio dell’Ottocento, come abbiamo detto, cambiò totalmente l’atteggiamento dei matematici nei confronti di questo V postulato. Abbandonata l’idea di dimostrarlo, si passò a costruire nuove geometrie assumendo postulati diversi, addirittura in contraddizione con quello di Euclide. Le ragioni possono essere ricercate nel ruolo ormai affievolito della geometria, non più considerata «fonte assoluta di certezza» a causa del progredire del ruolo dell’analisi matematica. La geometria apparve quindi come una scienza empirica. «Se fino allora le geometrie non euclidee erano considerate poco più che un gioco intellettuale senza grande interesse matematico, entrarono stabilmente a far parte del patrimonio della matematica moderna.» (Umberto Bottazzini: Il Sole 24 ore, 5-XI-1989). |
Il contributo di Riemann
Il contributo di Riemann fu essenziale, tanto che la nuova geometria portò presto il suo nome. Probabilmente Riemann non conosceva i lavori di Bolyai e di Lobachevsky, ma conosceva i dubbi di Gauss circa la verità e l’applicabilità senza discussione della geometria euclidea.
Riemann si propose tra l’altro di dimostrare che certi postulati di Euclide sono empirici e non delle verità evidenti di per sé, come si credeva. Secondo lui la via dell’analisi conduce alla certezza perché parte da elementi sicuri a priori, non da prove geometriche che possono ingannare la nostra percezione, dal momento che essa si basa su fatti non esplicitamente riconosciuti. Egli sviluppò così una geometria a n dimensioni pur sapendo che quella tridimensionale rispondeva già alle esigenze richieste.
Tale ampia concezione di spazi non euclidei e la conseguente preparazione del formalismo matematico necessario alla loro trattazione si trovano in una sua memoria presentata alla Società Matematica di Göttingen, ma pubblicata solo nell’anno successivo alla sua morte.  «In quella memoria – scrive Paolo Straneo dell’Università di Genova – Riemann trattò il problema della caratterizzazione degli spazi non euclidei più generali che allora si osasse concepire (e ora appunto si dicono riemanniani) estendendo ai continui a n dimensioni il criterio seguito da Gauss per l’analoga caratterizzazione dei continui a due sole dimensioni, cioè alle superfici. Al termine delle sue considerazioni si pone una domanda. Ci resta ora di rispondere alla questione: in quale misura e fino a che punto l’esperienza può confermare queste ipotesi? E conclude il suo lavoro osservando che un ulteriore sviluppo doveva necessariamente portare nel campo della fisica, dalla quale sola poteva giungere la conferma delle sue teorie. E questo accadde mezzo secolo dopo con la fisica einsteiniana.»
«In quella memoria – scrive Paolo Straneo dell’Università di Genova – Riemann trattò il problema della caratterizzazione degli spazi non euclidei più generali che allora si osasse concepire (e ora appunto si dicono riemanniani) estendendo ai continui a n dimensioni il criterio seguito da Gauss per l’analoga caratterizzazione dei continui a due sole dimensioni, cioè alle superfici. Al termine delle sue considerazioni si pone una domanda. Ci resta ora di rispondere alla questione: in quale misura e fino a che punto l’esperienza può confermare queste ipotesi? E conclude il suo lavoro osservando che un ulteriore sviluppo doveva necessariamente portare nel campo della fisica, dalla quale sola poteva giungere la conferma delle sue teorie. E questo accadde mezzo secolo dopo con la fisica einsteiniana.»
Un gruppo di matematici, infatti – tra cui ricordiamo gli italiani Gregorio Ricci Curbastro e Tullio Levi-Civita – sulla scia di Riemann diedero un tale assetto alla geometria degli spazi curvi, da renderla atta, all’inizio del XX secolo, a ricerche geometriche e fisiche del tipo di quelle che occorrevano a Einstein. La relatività generale trovò il suo supporto analitico. [Immagine sopra a sinistra: Gregorio Ricci Cubastro (1853-1925)] – [Immagine che segue a destra: Tullio Levi-Civita (1873-1940)] Una simpatica riflessione su questo argomento ci è offerta da uno storico della matematica, Eric T. Bell: «È possibile proporre una rappresentazione visibile di uno spazio curvo con più di due dimensioni, ma tale aiuto alla nostra percezione è utile quanto lo può essere un paio di rudimentali stampelle per un uomo senza piedi, poiché non aggiunge nulla alla comprensione e dal punto di vista matematico é inutile. Ma perché Riemann ha fatto tutto questo e come vi è giunto? È difficile tentare una risposta. Al più potremo dire che Riemann ha fatto quello che ha fatto, spinto dal suo demone, ma possiamo elencare i numerosi apporti al pensiero geometrico scaturiti dalla rivoluzione riemanniana. Prima di tutto questo ha permesso di creare un numero illimitato di “spazi” e di “geometrie” per scopi specifici – nella dinamica o nella geometria pura o nelle scienze fisiche – alla portata degli studiosi di geometria, e ha unificato quantità enormi di importanti teoremi geometrici collegandoli in gruppi che possono facilmente essere trattati come un tutto. In secondo luogo è stato chiarito il nostro concetto di “spazio” almeno nell’uso che di esso fanno i matematici e furono sollevati quegli ultimi brandelli di mistero che nascondevano la misteriosa non-entità dello spazio. I risultati di Riemann hanno insegnato ai matematici a diffidare di qualsiasi geometria, o di qualsiasi spazio, come una forma necessaria di percezione umana. Egli ha vibrato l’ultimo colpo di piccone allo spazio assoluto e il primo colpo agli altri “assoluti” della fisica del diciannovesimo secolo. Infine, la curvatura definita da Riemann, i procedimenti escogitati per studiare le forme differenziali quadratiche (che danno la formula del quadrato della distanza tra due punti vicini in uno spazio a n dimensioni), e il riconoscimento del fatto che la curvatura è un invariante, trovano tutti una brillante interpretazione nella teoria della relatività. Che la forma data da Riemann sia quella finale o meno, non ha importanza. Resta vero che senza il lavoro di Riemann sarebbe stata impossibile questa rivoluzione nel pensiero scientifico, a meno che un altro uomo successivamente fosse venuto a proporre quegli stessi concetti e metodi matematici creati da Riemann.» (Eric T. Bell, Men of mathematics, New York 1937).
Una simpatica riflessione su questo argomento ci è offerta da uno storico della matematica, Eric T. Bell: «È possibile proporre una rappresentazione visibile di uno spazio curvo con più di due dimensioni, ma tale aiuto alla nostra percezione è utile quanto lo può essere un paio di rudimentali stampelle per un uomo senza piedi, poiché non aggiunge nulla alla comprensione e dal punto di vista matematico é inutile. Ma perché Riemann ha fatto tutto questo e come vi è giunto? È difficile tentare una risposta. Al più potremo dire che Riemann ha fatto quello che ha fatto, spinto dal suo demone, ma possiamo elencare i numerosi apporti al pensiero geometrico scaturiti dalla rivoluzione riemanniana. Prima di tutto questo ha permesso di creare un numero illimitato di “spazi” e di “geometrie” per scopi specifici – nella dinamica o nella geometria pura o nelle scienze fisiche – alla portata degli studiosi di geometria, e ha unificato quantità enormi di importanti teoremi geometrici collegandoli in gruppi che possono facilmente essere trattati come un tutto. In secondo luogo è stato chiarito il nostro concetto di “spazio” almeno nell’uso che di esso fanno i matematici e furono sollevati quegli ultimi brandelli di mistero che nascondevano la misteriosa non-entità dello spazio. I risultati di Riemann hanno insegnato ai matematici a diffidare di qualsiasi geometria, o di qualsiasi spazio, come una forma necessaria di percezione umana. Egli ha vibrato l’ultimo colpo di piccone allo spazio assoluto e il primo colpo agli altri “assoluti” della fisica del diciannovesimo secolo. Infine, la curvatura definita da Riemann, i procedimenti escogitati per studiare le forme differenziali quadratiche (che danno la formula del quadrato della distanza tra due punti vicini in uno spazio a n dimensioni), e il riconoscimento del fatto che la curvatura è un invariante, trovano tutti una brillante interpretazione nella teoria della relatività. Che la forma data da Riemann sia quella finale o meno, non ha importanza. Resta vero che senza il lavoro di Riemann sarebbe stata impossibile questa rivoluzione nel pensiero scientifico, a meno che un altro uomo successivamente fosse venuto a proporre quegli stessi concetti e metodi matematici creati da Riemann.» (Eric T. Bell, Men of mathematics, New York 1937).
«La geometria non euclidea si è sviluppata fino a divenire uno strumento di grandissima utilità per le applicazioni al mondo fisico. Nella teoria della relatività, in ottica, e nella teoria generale della propagazione delle onde, talvolta è assai più adeguata una descrizione non euclidea dei fenomeni che non una descrizione euclidea.» (D. Hilbert e S. C.Vossen, Geometria intuitiva, Boringhieri ,Torino).
Topologia riemanniana
Un anno dopo la morte di Riemann è stata pubblicata una memoria da lui presentata qualche anno prima alla Società Matematica di Göttingen, sugli spazi non euclidei. Si tratta di un esposto molto profondo ma altrettanto conciso e di difficile interpretazione.
Egli trattò il problema della caratterizzazione degli spazi non euclidei molto generali, estendendo ai continui a n dimensioni il criterio seguito da Gauss per l’analoga caratterizzazione dei continui a due sole dimensioni, cioè alle superfici.  Si tratta di una nozione non intuibile per la nostra mentalità, ma si esprime dicendo che quei continui stanno in ogni intorno di un loro punto a un analogo intorno di un continuo euclideo, come un elemento di superficie sta a un elemento di piano. Definizione manifestamente oscura e contorta. Formalmente però è possibile esprimere il concetto con l’analisi riemanniana.
Si tratta di una nozione non intuibile per la nostra mentalità, ma si esprime dicendo che quei continui stanno in ogni intorno di un loro punto a un analogo intorno di un continuo euclideo, come un elemento di superficie sta a un elemento di piano. Definizione manifestamente oscura e contorta. Formalmente però è possibile esprimere il concetto con l’analisi riemanniana. 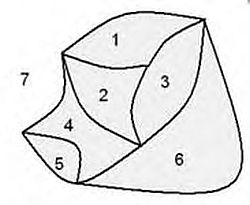 Altro concetto astratto piuttosto difficile è quello di superficie di Riemann. Essa è composta da due o più fogli, ognuno dei quali rappresenta un ramo di una funzione di una variabile complessa. Una superficie riemanniana di una curva algebrica f(x,y) = 0 pensata sul piano complesso è una superficie reale che dal punto di vista topologico risulti omeomorfa alla curva data.
Altro concetto astratto piuttosto difficile è quello di superficie di Riemann. Essa è composta da due o più fogli, ognuno dei quali rappresenta un ramo di una funzione di una variabile complessa. Una superficie riemanniana di una curva algebrica f(x,y) = 0 pensata sul piano complesso è una superficie reale che dal punto di vista topologico risulti omeomorfa alla curva data.
L’Analysis Situs o topologia, si è sviluppata sui fondamenti delle teorie di Riemann. La topologia si occupa, dal punto di vista elementare, della classificazione delle superfici in base alla connettività, ossia in base al numero di linee chiuse che vi possono essere tracciate senza disgiungerle in due parti distinte.(1)
Argomenti di topologia sono, per esempio, il problema dei quattro colori delle carte geografiche; il nastro di Möbius a una sola faccia [Immagine sopra a sinistra]; il problema di congiungere un certo insieme di punti con un altro insieme diverso attraverso sentieri che non si intreccino; il grafo di Eulero [Immagine sopra a destra (2)]; il problema dei sette Ponti di Königsberg [Immagine che segue]; eccetera.
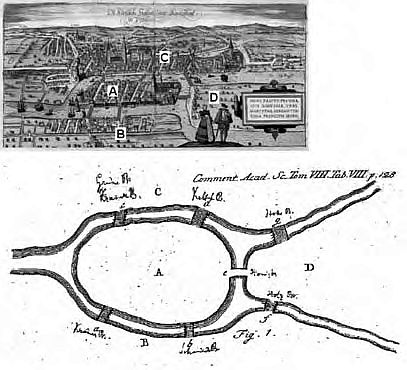 Esempio di problema topologico: i sette ponti di Könisberg.
Esempio di problema topologico: i sette ponti di Könisberg.
Come spiega Eulero nel suo Commentarius all’Accademia delle Scienze, è impossibile fare una passeggiata in cui si attraversi ogni ponte una e una sola volta. Sarebbe possibile solo se da ciascuna isola (vertice) A, B, C, D uscisse un numero pari di lati.
Tali ricerche connesse con elevati problemi di analisi e di algebra hanno avuto un enorme sviluppo in questi ultimi decenni.
Riemann e la scienza oggi
Dopo questa panoramica sulla vita e l’opera di Bernhard Riemann sorge spontanea la domanda: quale influenza ha avuto Riemann sullo sviluppo successivo della matematica e della scienza in genere? Egli è, fuor di dubbio, uno dei più grandi matematici d’ogni tempo, e le sue concezioni hanno influenzato diversi campi della matematica; ma non dobbiamo dimenticare che lo sviluppo matematico è conseguenza anche di chi lo ha preceduto. Esiste nello sviluppo delle scienze una continuità che ha tuttavia bisogno di grandi ricercatori per progredire e arricchirsi.
Egli è, fuor di dubbio, uno dei più grandi matematici d’ogni tempo, e le sue concezioni hanno influenzato diversi campi della matematica; ma non dobbiamo dimenticare che lo sviluppo matematico è conseguenza anche di chi lo ha preceduto. Esiste nello sviluppo delle scienze una continuità che ha tuttavia bisogno di grandi ricercatori per progredire e arricchirsi.
Riemann è stato definito dal matematico Klein «un ricercatore la cui influenza è stata senza uguali nello sviluppo delle matematiche moderne […] come pure nella meccanica e nella fisica teorica. – e aggiunge – tutto questo è unicamente la conseguenza della incomparabile potenza delle sue concezioni matematiche tanto originali e profonde.» (Felix Klein, Discorso al Versammlung deutscher Naturforscher und Aerzte). [Immagine qui sopra a sinistra: Felix Klein (1849-1925)]
Raccogliamo qui alcune indicazioni relative ai campi della scienza ove principalmente è stata decisiva la sua influenza.
La Teoria delle Funzioni di una variabile complessa ha portato a interpretare le funzioni già note, in modo più comprensibile e fecondo di quanto già non fosse coi vecchi metodi. Da allora la teoria delle funzioni ha progredito lungo la linea riemanniana. Egli ha applicato i teoremi fondamentali della teoria del potenziale, e cioè il suo punto di partenza è stato il campo della fisica – matematica, cosa che è diventata oggi di uso corrente, nello studio dei fenomeni elettrici e in tutti i rami della fisica – matematica.
I metodi che Riemann ha escogitato partendo dalla intuizione fisica per applicarli alla matematica pura, si sono dimostrati importantissimi nel senso inverso per lo studio della fisica-matematica: i principi di Riemann hanno un vastissimo campo di applicazione. Problemi che sembravano insolubili hanno trovato così facili soluzioni; si pensi solo al problema di Helmholtz relativo alla forma di una lamina liquida libera, o alla teoria delle superficie minime di dato contorno.
Le teorie riemanniane hanno portato a soluzioni brillanti rispettivamente alle equazioni differenziali, alle funzioni algebriche, alla geometria sintetica, alla trasformazione generale univoca, agli integrali, eccetera. La gloria di Riemann va ricercata nelle basi che ha posto per lo studio delle tre grandi categorie di funzioni: trascendenti, ellittiche, ipergeometriche.
Scrisse Klein a proposito delle funzioni che lui stesso ha studiato e che ha chiamato funzioni automorfe: «Tali sviluppi di cui oggi si occupano coloro che scelgono come argomento di approfondimento la teoria delle funzioni automorfe si trovano in una forma generale più o meno esplicita nei manoscritti che Riemann ci ha lasciato.»
La legge della distribuzione dei numeri primi nella serie naturale dei numeri è stata intuita da Riemann e da lui dimostrata solo parzialmente. Diversi matematici si sono cimentati per completarne la dimostrazione, ma non sono arrivati più in là. Riemann l’ha dedotta dalla intuizione fisica: essa si è affermata come ottimo metodo euristico e trova la sua conferma nella realtà.
I frammenti e gli appunti che Riemann ci ha lasciato e che per l’immatura morte non ha potuto sviluppare, non sono stati meno fecondi nella storia della matematica moderna.
Si tratta di contributi la cui «influenza è dominante e determinante per lo sviluppo e il progresso della scienza» (Klein).
Riemann ha dato una forma nuova ed elegante alle ricerche di Gauss, Bolyai e Lobacevsky sul V postulato di Euclide e la possibilità di costruire una geometria generale perfettamente logica, di cui quella tradizionale rappresenta solo un caso particolare. Da qui è arrivato alla nuova teoria di uno spazio curvo che ha portato dopo mezzo secolo alle ardite concezioni einsteiniane. Egli ha aperto così una finestra su un mondo sconosciuto che interessa tanto la filosofia quanto la geometria, e che dimostra una straordinaria capacità di astrazione dell’autore.
I contributi scientifici di Riemann che gli storici della matematica scoprono non sono facilmente intuibili ai non addetti ai lavori; essi sono soprattutto apprezzati dagli specialisti, data la profondità e la difficoltà degli argomenti. Anche gli studiosi di analisi e di geometria si stanno sempre più servendo delle sue teorie per rinnovare i loro metodi di indagine. Dobbiamo inoltre riconoscergli il merito di aver sollecitato la ricerca matematica in Italia nella seconda metà del secolo scorso, soprattutto a partire dai suoi amichevoli contatti con Enrico Betti, Felice Casorati e Francesco Brioschi.
Ma fu soprattutto Albert Einstein che ebbe modo di apprezzare e di utilizzare le idee anticipatrici di Riemann. Einstein poté passare dalla teoria della relatività ristretta del 1905 alla relatività generale dieci anni dopo, grazie ai lavori di Riemann. Gli mancava l’algoritmo, lo strumento matematico per dare un assetto tecnico alle sue concezioni, e si dedicò a un approfondito studio dei formalismi della matematica pura avanzata. Trovò la chiave nei lavori di Riemann. Si accorse che la geometria euclidea tradizionale non era sufficiente a dare una descrizione appropriata della realtà fisica; occorreva una geometria riemanniana più generale. Fu così che Riemann fornì con la sua matematica la lingua dello spazio curvo di cui Einstein aveva bisogno.
Da Riemann è partito lo sforzo per la formulazione della unificazione delle leggi fisiche. Cresciuto alla scuola di Gauss e Weber – matematici e fisici – egli ha sempre lavorato alla ricerca di una forma matematica che esprimesse in modo unico le leggi cui ubbidiscono i fenomeni naturali della elettricità, del magnetismo, dell’ottica, della termodinamica e persino della gravità. Tale ricerca ha portato, con Maxwell, alla teoria elettromagnetica della luce e con Einstein, nel marzo del 1953, alla geniale formulazione di quattro equazioni rivoluzionarie che dovrebbero costituire «la chiave dell’universo». Con tale teoria il grande scienziato avrebbe trovato una legge unitaria valida per i fenomeni del macrocosmo e quelli del microcosmo che sembrano per ora governati da leggi diverse.
Questa teoria, ancora embrionale, gli richiedeva secondo le sue stesse parole, almeno venti anni per essere chiarita e completata. Egli morì due anni dopo; altri fisici, anche italiani, si sono cimentati; i venti anni sono passati e la soluzione non è giunta ancora. Resta vero però che odierni ulteriori tentativi di unificazione teorica fanno tuttora affidamento su geometrie astratte che hanno origine nelle ardite visioni riemanniane  In definitiva, l’apprezzamento profetico di M. Hermite, nella introduzione alla pubblicazione in francese delle opere di Riemann (Oeuvres Mathématiques de Riemann, Gauthier-Villars, Ecole Polytechnique, Paris), si è pienamente attuato. Scrive infatti: «L’opera di Bernhard Riemann è a tutt’oggi la più bella e la più grande dell’Analisi; è stata consacrata dalla ammirazione unanime, e lascerà una traccia imperitura nella scienza. Gli studiosi contemporanei di geometria nei loro lavori si ispirano alle sue concezioni, e con le loro scoperte ne rilevano ogni giorno l’importanza e la fecondità. Questo illustre matematico ha aperto una nuova era che reca l’impronta del suo genio.» [Immagine a destra: Charles Hermite (1822-1901)]
In definitiva, l’apprezzamento profetico di M. Hermite, nella introduzione alla pubblicazione in francese delle opere di Riemann (Oeuvres Mathématiques de Riemann, Gauthier-Villars, Ecole Polytechnique, Paris), si è pienamente attuato. Scrive infatti: «L’opera di Bernhard Riemann è a tutt’oggi la più bella e la più grande dell’Analisi; è stata consacrata dalla ammirazione unanime, e lascerà una traccia imperitura nella scienza. Gli studiosi contemporanei di geometria nei loro lavori si ispirano alle sue concezioni, e con le loro scoperte ne rilevano ogni giorno l’importanza e la fecondità. Questo illustre matematico ha aperto una nuova era che reca l’impronta del suo genio.» [Immagine a destra: Charles Hermite (1822-1901)]
Conclusione
Tutti gli studiosi riconoscono che le ipotesi e gli sviluppi delle idee di Riemann in ogni campo da lui trattato, sono originali e personali: il suo genio non deve niente a nessuno. Lui stesso probabilmente non ha misurato la fecondità delle sue teorie, né previsto tutte le conseguenze che ne derivano.
Eccone una prova come esempio: «La teoria generale della relatività ci ha insegnato che alla base di una descrizione appropriata della realtà fisica non può essere posta l’ordinaria geometria euclidea, ma una geometria riemanniana più generale.» (D. Hilbert e S.C. Vossen, Geometria intuitiva, Boringhieri, Torino).
Dalle ardite concezioni di Riemann ebbe origine un gran numero di possibili geometrie generali fino ad oggi non ancora completamente esplorate.
«Le ormai note geometrie non euclidee ne rappresentano solo un esempio importante ma non esaustivo. Con le scoperte di Riemann è cambiata la situazione della geometria. Le sue basi non sono più costituite da assiomi immediatamente intuitivi e comprensibili di per sé, ma da ipotesi, ed è cosi svanita la speranza di conoscenze assolutamente sicure anche nel campo della geometria. Ma in compenso Bernhard Riemann ha fornito, con la sua matematica, la lingua dello spazio curvo di Einstein.» (Roman Sexl: Ciò che tiene assieme il mondo, Zanichelli, 1990).
E tale lingua ha appena cominciato a parlare.
Pietro Monti
(Docente di Matematica presso l’Istituto “Santa Maria” di Verbania, membro dell’Associazione Mathesis sezione di Verbania)
Vai all’articolo in formato PDF
Note
- Due lettere di Enrico Betti al collega Placido Tardy (1816-1914), riprodotte da André Weyl (1906-1998) in Archive for History of Exact Sciences, 20, 91 (1979) sotto il titolo Riemann, Betti and the Birth of Topology, illustrano assai bene il ruolo di Riemann e dello stesso Betti nello sviluppo della topologia.
La seconda lettera (16 ottobre 1863) inizia così: «Mio caro Placido, Riemann dimostra, con molta facilità, che si può ridurre uno spazio qualunque ad essere semplicemente connesso, mediante sezioni lineari e sezioni superficiali semplicemente connesse.[…]». - Il grafo di Eulero. Un grafo connesso planare disegnato nel piano con v vertici (6 in questo caso), f aree (7 in questo caso, contando anche quella esterna), ed e linee di bordo (11 in questo caso) soddisfa sempre la relazione di Eulero: v − e + f = 2.
© Pubblicato sul n° 40 di Emmeciquadro
