Come afferma l’autore, «pur essendo a tutti nota, attraverso l’esperienza» la temperatura è una grandezza tale che «la maggior parte di noi non saprebbe definirla». Partendo da questa considerazione viene svolto un percorso definitorio che, partendo dal concetto di equilibrio termico, fa un uso del linguaggio matematico (classi di equivalenza) per introdurre un concetto generale di temperatura, che poi viene precisato da un punto di vista fisico attraverso un procedimento sperimentale.
Fra le grandezze fisiche la temperatura è forse quella che più di ogni altra ci riguarda quotidianamente in vari aspetti della nostra vita: gioca un ruolo essenziale nella cottura dei cibi, dalla temperatura dell’aria dipende in gran parte il nostro stato di benessere fisico e la temperatura corporea è un indicatore primario del nostro stato di salute.
Nella vita del nostro pianeta e dell’Universo è ancora la temperatura la protagonista: il riscaldamento globale della Terra è una minaccia per lo scioglimento dei ghiacciai della zona artica, che avrebbe conseguenze disastrose a livello planetario, e ancora la temperatura ha scandito le diverse fasi dell’evoluzione dell’Universo dopo il Big Bang: dai 100000 miliardi di miliardi di miliardi di gradi Kelvin (1032 K) dell’istante iniziale di massima energia e densità del cosmo, quando ancora esisteva un’unica forza fondamentale, alla temperatura di 10000 miliardi di gradi Kelvin (1013 K) che consentì la completa differenziazione delle quattro forze fondamentali (gravità, interazione nucleare forte e debole, forza elettromagnetica), nonché la comparsa del protone e quindi della materia. Insomma, non v’è fenomeno, dal più semplice al più complesso, che non ci faccia imbattere in questa grandezza della fisica.
Il fatto strano è che pur essendo a tutti nota, attraverso l’esperienza, tuttavia la maggior parte di noi non saprebbe definirla, quasi come accade per un’altra grandezza fisica fondamentale: il tempo.
La temperatura: una grandezza fisica sui generis
Come è noto, una grandezza fisica è tale se per essa si possono stabilire inequivocabilmente una unità di misura e un criterio di uguaglianza e somma (e differenza) in modo da poter definire una procedura di misura.
La temperatura, pur essendo accettata come grandezza fisica, in realtà non possiede completamente tali requisiti. Infatti, non è possibile definire una unità di misura della temperatura bensì soltanto dell’intervallo di temperatura, analogamente a quanto accade per il tempo. Inoltre non gode della proprietà additiva.
Mentre, per esempio, fissata l’unità di lunghezza è possibile «costruire» qualunque altra lunghezza allineando un sufficiente numero di volte la lunghezza unitaria e i suoi sottomultipli, ciò invece non accade con la temperatura: non è possibile, con lo stesso metodo additivo, realizzare per esempio una temperatura tripla dell’unità di temperatura perché, se si mettessero a contatto tre corpi con temperatura unitaria, per il principio dell’equilibrio termico (vedi oltre in questo articolo) il corpo risultante dalla loro unione avrebbe ancora temperatura unitaria.
Per tali ragioni non è possibile stabilire un numero discreto di multipli e sottomultipli della temperatura che ne consentano una misura relativa come per le altre grandezze, bensì è necessario fissare «ogni suo multiplo e sottomultiplo» stabilendo arbitrariamente una scala numerica delle temperature e uno zero, ovvero un punto di riferimento reso necessario del fatto che si possono considerare soltanto intervalli di temperatura1.
Queste sue caratteristiche, che ne fanno una grandezza fisica atipica, sono dovute al fatto che non è possibile accedere direttamente alla temperatura per misurarla, bensì occorre considerare i suoi effetti su qualche altra grandezza fisica, come accade nei comuni termometri a mercurio, che danno una misura della temperatura attraverso la dilatazione subita dal mercurio in un tubicino di vetro2.
Più che una vera grandezza fisica, quindi, la temperatura deve essere considerata un indice dello stato termico di un corpo, cioè di quel suo particolare stato che noi percepiamo con le sensazioni di caldo e freddo: «Si chiama temperatura una grandezza fisica che misura quanto un corpo è caldo o freddo»3 dice Enrico Fermi. Ma è chiaro che definizioni come questa sono in realtà soltanto pseudo-definizioni, utili soltanto per focalizzare il significato fisico intuitivo della temperatura, come quest’altra: «… la temperatura d’un corpo è quello stato suo particolare pel quale, essendo esso posto a contatto degli altri corpi, può cedere loro calore o riceverne»4.
Le grandezze fondamentali della fisica
Le grandezze fondamentali della fisica (lunghezza, massa, tempo, temperatura) ricoprono un ruolo analogo a quello degli enti primitivi nella geometria: sono infatti le grandezze dalle quali sono derivate tutte le altre grandezze fisiche, così come dal punto, dalla retta e dal piano sono derivate tutte le figure della geometria euclidea.
In tal modo basta fissare (con un certo arbitrio) le unità di misura delle sole grandezze fondamentali tramite dei campioni fisici e derivare le unità di misura di tutte le altre grandezze (dette derivate) analiticamente per mezzo delle relazioni che le legano a quelle fondamentali.
Come gli enti primitivi della geometria, esse sono quindi indefinite ma soltanto dal punto di vista fisico, mentre possono essere definite al di fuori della fisica. Un esempio è la lunghezza, che come grandezza fisica fondamentale non implica la definizione di altre grandezze fisiche, ma matematicamente è invece definibile come classe di equivalenza rispetto alla relazione di congruenza fra segmenti dello spazio euclideo. Insomma il concetto di lunghezza in fisica è ereditato dalla geometria e viene soltanto completato dal punto di vista fisico «materializzandolo» (perdendo quindi il carattere puramente ideale che ha in geometria) e fissando un campione fisico della sua unità di misura.
Anche per la temperatura è possibile darne una definizione matematica che non coinvolga altre grandezze fisiche. Tuttavia, a differenza della lunghezza, la definizione matematica della temperatura deve necessariamente trarre spunto da considerazioni sperimentali, le quali però implicano soltanto concetti meccanici, cosicché è scongiurato il rischio di una petitio principii che si verificherebbe se presupponesse il concetto stesso di temperatura. Inoltre tale definizione è indipendente da tutte le possibili procedure di misurazione della temperatura, che conducono a molteplici scale termometriche, ciascuna dipendente dal corpo termometrico, dalla proprietà termometrica e dalla relazione funzionale, necessariamente arbitraria, fra questa e la temperatura.
Pertanto, la definizione matematica di temperatura non può definire da sola la temperatura come grandezza fisica perché non è una definizione strumentale come richiesto dalla fisica5, ma fornisce una definizione di temperatura generica valida qualunque sia poi il suo completamento dal punto di vista operativo, che può condurre a due tipi di temperature: le temperature empiriche e la temperatura termodinamica. Essa ha dunque un valore concettuale, esente da tutte le limitazioni che caratterizzano le varie definizioni operative della temperatura. Nel seguito indicheremo con θ la temperatura generica.
Vediamo assieme come ciò sia possibile, attraverso un viaggio ideale dalla fisica alla matematica con ritorno alla fisica.
Dalla fisica alla matematica
Premessi i concetti di sistema termodinamico, stato termodinamico e stato termodinamico di equilibrio, definiamo cosa si intende per stati in equilibrio termico.
Tre concetti preliminari per una definizione di temperatura Un sistema termodinamico è una qualsiasi porzione di materia di dimensioni finite e pertanto tale da potersi pensare costituita da un numero rilevante di particelle il cui comportamento statistico determina il suo stato macroscopico. |
Si considerino due sistemi A e B isolati dall’esterno tramite una parete adiabatica, che non permette scambi di energia sotto nessuna forma (e quindi anche di calore), e separati fra loro da una parete diatermica, che invece consente gli scambi di calore6. L’esperienza mostra che se gli stati fisici iniziali di A e B sono differenti, essi mutano in due nuovi stati di equilibrio caratterizzati da due nuove ennuple di variabili (Xa, Ya, …; Xb, Yb, …) in generale differenti fra loro ma non indipendenti7. I due nuovi stati di A e B si dicono in equilibrio termico e definiscono entrambi lo stato di equilibrio termico del sistema complesso ![]() attraverso la relazione che lega fra loro le grandezze di stato dei due sistemi A, B:
attraverso la relazione che lega fra loro le grandezze di stato dei due sistemi A, B:
F(Xa, Ya, … Xb, Yb, …) = 0 [1]
Da tali considerazioni di natura sperimentale segue che ogni sistema è in equilibrio termico con se stesso (proprietà riflessiva dell’equilibrio termico) e che se il sistema A è in equilibrio termico con il sistema B, anche B è in equilibrio termico con A (proprietà simmetrica dell’equilibrio termico).
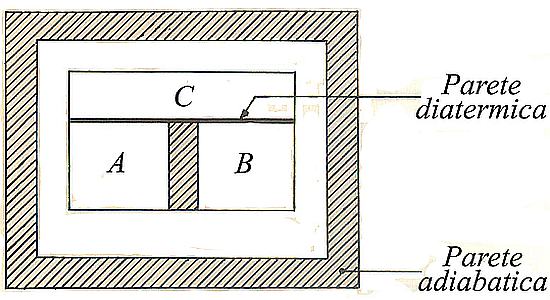
Inoltre, considerati due sistemi A e B isolati dall’esterno e fra loro tramite pareti adiabatiche, si aggiunga a essi un terzo sistema C separato dai primi due tramite una parete diatermica (si veda l’immagine che segue). Atteso un opportuno intervallo di tempo, i sistemi A e B risulteranno in equilibrio termico con C. Sostituendo allora la parete adiabatica che isola A da B con una diatermica, si constata che pure A e B sono in equilibrio termico, in quanto gli stati di A e di B rimangono invariati. È questo il principio zero della termodinamica8 o principio dell’equilibrio termico, il quale consente di asserire che la relazione di equilibrio termico gode anche della proprietà transitiva ed è quindi una relazione di equivalenza.
In pratica, per riconoscere se due o più stati sono in equilibrio termico, non si effettua l’esperimento precedentemente illustrato, che risulterebbe scomodo e di difficile attuazione, ma si ricorre a un termoscopio. Questo è uno strumento che non dà la misura della temperatura ma semplicemente consente di confrontare due stati termici stabilendo se sono in equilibrio o no, in base alle variazioni subite da una proprietà qualunque che dipenda dallo stato termico (proprietà termometrica). Se per esempio la proprietà termometrica è l’altezza di una colonna di liquido, per affermare che gli stati termici di due sistemi sono in equilibrio basta porre a contatto termico successivamente il termoscopio con i due sistemi e verificare che l’altezza della colonna liquida risulti uguale nei due casi.
Associando la relazione di equilibrio termico R all’insieme S di tutti i possibili stati di equilibrio termico di uno stesso sistema o di sistemi diversi9, risulta definita una partizione Θ di S in classi di equivalenza, costituite da stati in equilibrio termico, pervenendo all’insieme quoziente ![]() : ogni classe θ di equivalenza di tale insieme è una temperatura.
: ogni classe θ di equivalenza di tale insieme è una temperatura.
Ne segue che tutti gli stati che sono in equilibrio termico appartengono a una medesima classe di Θ e quindi hanno la medesima temperatura e viceversa se due stati hanno la stessa temperatura appartengono alla stessa classe di Θ e quindi sono in equilibrio termico.
Il principio di contrazione, o passaggio al quoziente, consente dunque di formulare la seguente definizione: una temperatura è una classe di equivalenza rispetto alla relazione di equilibrio termico fra gli stati termodinamici di uno stesso sistema o di sistemi diversi.
Passaggio al quoziente Relazione di equivalenza: gode delle proprietà riflessiva, simmetrica e transitiva. |
Può generare un certo scetticismo e sembrare paradossale la sostituzione, accettata dalla matematica, di una proprietà comune a più elementi (che sia però una relazione di equivalenza) con la classe di tali elementi. Così accade nella definizione testé data di temperatura: ogni stato di una stessa classe dell’insieme quoziente Θ ha in comune con tutti gli altri stati della stessa classe la proprietà di essere in equilibrio termico con essi.
Bertrand Russell ha accuratamente analizzato la questione, concludendo: «Ogni volta che la matematica deriva una proprietà comune da una relazione riflessiva, simmetrica e transitiva, tutti gli scopi matematici della proprietà supposta vengono pienamente raggiunti sostituendo a essa la classe dei termini che hanno la relazione data con un dato termine»10.
Taluni autori forniscono, invece, una definizione implicita per astrazione della temperatura, utilizzando ancora una volta la relazione di equilibrio termico: la temperatura θ viene definita come quella proprietà attinente a un sistema tale che i suoi valori assunti in corrispondenza di due stati A e B sono uguali se e solo se A e B sono in equilibrio termico:
θ(A) = θ(B) ![]() A e B in equilibrio termico
A e B in equilibrio termico
Le definizioni implicite però, come è noto, non precisano la natura dell’ente che definiscono e quelle implicite per astrazione che fanno uso di una relazione di equivalenza R, in particolare, non ne assicurano nemmeno l’unicità, in quanto la R caratterizza non soltanto la proprietà o funzione φ(x) che si vuol definire ma anche ogni altra funzione di questa f [φ(x)]11.
Si richiama l’attenzione sulla differenza sostanziale, e non soltanto formale, fra le definizioni per astrazione e per classi, le quali, utilizzando entrambe la medesima relazione di equivalenza, possono essere confuse fra loro.
La prima definisce l’ente indirettamente, in maniera implicita, come quella proprietà che è comune a tutti gli elementi di una stessa classe generata da una relazione di equivalenza applicata a un certo insieme: la temperatura è la proprietà comune a tutti gli stati in equilibrio termico che, come tali, appartengono alla stessa classe di equivalenza. La temperatura così definita è un concetto astratto.
La seconda invece definisce direttamente, in maniera esplicita, l’ente identificandolo con una classe di elementi generata da una relazione di equivalenza applicata a un certo insieme: una temperatura è una classe (di equivalenza) di stati termodinamici, di uno stesso sistema o di sistemi diversi, in equilibrio termico fra loro. La temperatura così definita è un concetto-classe.
Il passaggio al quoziente mediante il quale si è fornita la precedente definizione esplicita per classi della temperatura istituisce tra l’insieme S di tutti i possibili stati termodinamici di un sistema (o di sistemi diversi) e l’insieme Θ delle classi di stati in equilibrio termico una mappa univoca di S in Θ:
F : S → Θ ovvero θ = θ(s) [2]
La quale associa ad ogni stato termodinamico s ε S una e una sola classe θ ε Θ di stati in equilibrio termico con s, ovvero una e una sola temperatura.
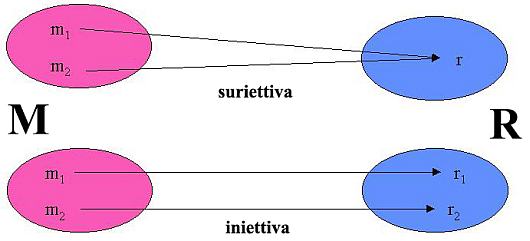
La relazione precedente è una mappa suriettiva poiché ogni elemento di Θ è il corrispondente di almeno un elemento di S, ma non iniettiva e quindi non biunivoca, in quanto ogni elemento di Θ è il corrispondente di infiniti elementi di S, ovvero a ogni temperatura corrispondono infiniti stati termodinamici diversi in equilibrio termico.
Funzioni suriettive e iniettive Una applicazione f : M → R è suriettiva se ogni elemento di R è il corrispondente di almeno un elemento di M, ovvero se il codominio f(M) si identifica con l’insieme R: f(M) = R; è iniettiva se a ogni coppia di elementi diversi di M corrispondono elementi diversi di R:
|
Per esempio, per la legge di Boyle, in un gas perfetto12 mantenuto a temperatura costante, il volume e la pressione variano secondo la relazione P1V1=P2V2=…=PnVn. Dunque, a una medesima temperatura corrispondono infiniti stati diversi in equilibrio termico: (P1, V1); (P2, V2);…;( Pn, Vn) [n → ∞] .
Ritorno alla fisica
Per definire la temperatura come grandezza fisica, però, occorre stabilire operativamente come misurarla, ovvero come assegnare un valore numerico di temperatura a ogni classe di infiniti stati in equilibrio termico. Non tratteremo e discuteremo qui i vari procedimenti di misura della temperatura perché ciò esulerebbe dalle finalità di questo articolo entrando in un ambito prettamente fisico. Ci limiteremo soltanto a evidenziare le linee guida del ragionamento che dalla definizione matematica di temperatura generica può condurre a una definizione fisica operativa, trascurando quindi tutti i dettagli più tecnici, a beneficio dell’attenzione verso i più profondi legami fra matematica e fisica.
Se in luogo dello stato termodinamico s si pone la ennupla delle variabili Xi (i = 1,2,3,…,n) che lo definiscono, la relazione [2] si può scrivere anche:
θ = θ(Xi) [3]
In uno spazio euclideo n-dimensionale En il luogo dei punti di coordinate Xi è una superficie che rappresenta geometricamente gli infiniti stati termici di un sistema termodinamico.
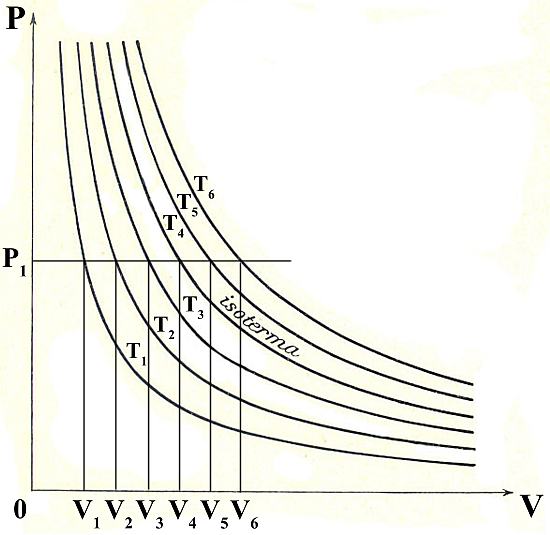
Nel caso particolare dei fluidi, in cui le variabili di stato sono pressione P, volume V e temperatura T, si ha una superficie dell’ordinario spazio euclideo E3. Se consideriamo un piano di equazione T=T1 (con T1 costante) esso intersecherà tale superficie in una curva detta isoterma poiché rappresenta geometricamente gli infiniti stati del sistema aventi tutti quella temperatura.
Variando lo stato termico (e quindi la temperatura) di un corpo si ottiene per esso una serie di isoterme; le isoterme dei diversi corpi corrispondenti a una data temperatura θ1 rappresentano quindi geometricamente gli infiniti stati in equilibrio termico aventi la temperatura θ1 ovvero costituiscono l’immagine geometrica della temperatura θ1.
È da notare che la costruzione di ogni isoterma non richiede la conoscenza della sua temperatura, ma soltanto la misura di variabili di stato diverse dalla temperatura (nel caso dei gas perfetti la pressione e il volume) in distinti stati termici in equilibrio, validati come tali da un termoscopio qualunque. Ovviamente, così facendo, si può dire soltanto che ogni isoterma di un corpo (o la serie delle isoterme corrispondenti di più corpi) è relativa a una certa temperatura di cui per il momento rimane indeterminato il valore numerico, che potrà essere noto soltanto fissando una procedura di misura della temperatura, che consiste nello stabilire una scala numerica scegliendo un particolare corpo di riferimento, che costituisce il termometro campione primario, e un criterio per assegnare un valore numerico diverso a ogni sua isoterma13. La misura della temperatura di un corpo, concettualmente, sarà l’indicazione di tale termometro campione a equilibrio termico raggiunto con il corpo in misura, in quanto i loro stati termici risultando in equilibrio termico hanno per definizione la stessa temperatura.
Per ottenere ciò è necessario far diventare iniettiva la funzione θ = θ(Xi), in modo che ogni temperatura θ sia la corrispondente di un solo stato termico definito dalla e-nnupla Xi, per modo che accanto alla mappa (2) si possa considerare la mappa inversa f -1: Θ → S, stabilendo così una corrispondenza biunivoca S ↔ Θ fra gli stati termici e le temperature.
Dal punto di vista fisico ciò si realizza se sono verificate due condizioni. La prima è che nella trasformazione termodinamica che porta il termometro campione all’equilibrio termico con il corpo in misura vari soltanto una delle variabili di stato (corrispondente alla proprietà termometrica) mantenendo costanti le rimanenti. La seconda è che ogni isoterma individui un solo valore della proprietà termometrica.
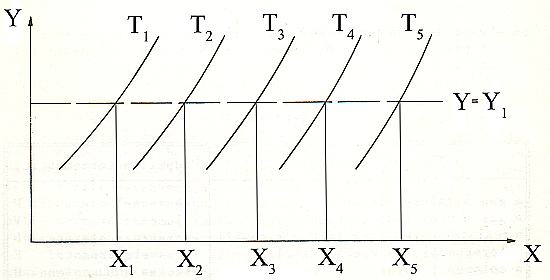
Tali considerazioni risultano evidenti nel caso in cui il corpo termometrico sia a tre variabili di stato X,Y,T (per es. un fluido), per il quale le isoterme (nel piano X,Y) devono essere curve crescenti o decrescenti: la retta Y = Y1 parallela all’asse delle X interseca allora ciascuna isoterma in un solo punto, evidenziando una corrispondenza biunivoca fra la proprietà termometrica X e le isoterme e quindi le temperature.
Nel caso dei gas perfetti, per esempio, le isoterme nel piano P,V (piano di Clapeyron) sono iperboli equilatere (si veda l’immagine che segue). Alla pressione P1 costante le isoterme T1, T2, T3, …Tn risultano in corrispondenza biunivoca con i valori V1, V2, V3,…,Vn della proprietà termometrica volume.
La relazione [3] diviene allora una mappa biunivoca (funzione termometrica) che associa a ogni valore della proprietà termometrica una e una sola temperatura e viceversa:
θ = θ(X) [3]’
E fornisce la curva di graduazione del termometro campione, consentendo di ricavare le misure della temperatura dai valori della proprietà termometrica X. Tale relazione, ovviamente, può essere fissata soltanto arbitrariamente.
Per convenzione si sceglie una funzione termometrica lineare θ(X) = a X (con a costante). Fissato uno stato di riferimento e indicati con Xo e con θ(Xo) i corrispondenti valori della proprietà termometrica e della temperatura, si ottiene a = θ(Xo)/Xo e quindi:
![]() [4]
[4]
Dal 1954 si assume come stato di riferimento il punto triplo dell’acqua pura alla pressione di 1 atm e si assegna alla corrispondente temperatura il valore θ(Xo)=273,1614. Con tali assunzioni, la [4] diventa:
![]() [4]’
[4]’
Essendo Xo e X i valori assunti dalla proprietà termometrica rispettivamente in corrispondenza del punto triplo dell’acqua e una volta raggiunto l’equilibrio termico fra il termometro campione e il corpo in misura.
Il termometro campione primario, per convenzione internazionale, è costituito da un termometro a gas nel quale il volume del gas è mantenuto costante e la proprietà termometrica è la pressione P.
Con tali assunzioni la [4]’ si scrive:
![]() [5]
[5]
Essendo Po e P la pressione del gas in corrispondenza del punto triplo dell’acqua e quella del gas nel termometro in equilibrio termico con il corpo in misura.
La relazione [5] applicata a gas reali differenti fornisce altrettante scale termometriche empiriche, non consentendo in tal modo di definire un’unica scala termometrica cui fare riferimento a livello internazionale. L’esperienza, però, dimostra che anche utilizzando gas reali diversi ma sempre più rarefatti, e quindi con valori di P0 sempre più piccoli (tendenti a zero), le temperature misurate con i rispettivi termometri tendono tutte allo stesso valore limite.
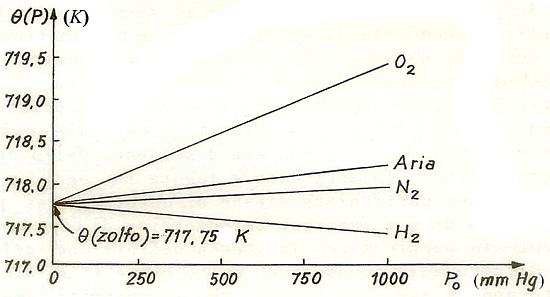
Nell’immagine precedente, dove sono riportate, in funzione di P0, le temperature di condensazione dello zolfo ottenute con termometri a pressione utilizzanti quattro gas diversi (ossigeno, aria, azoto, idrogeno), si vede chiaramente che mentre per valori di P0 lontani dallo zero le misure possono divergere anche di qualche grado Kelvin, al tendere a zero di P0 tutti i termometri tendono a indicare la stessa temperatura di 717,75 K.
Poiché più rarefatto è un gas reale più esso approssima il modello del gas perfetto, possiamo allora concludere che la:
![]() [5]’
[5]’
Può definire formalmente un’unica scala termometrica di riferimento detta scala termometrica normale, tramite un termometro campione che impieghi un gas perfetto, mantenuto a volume costante, e di cui si lasci variare la pressione. Per convenzione si impiega l’idrogeno sufficientemente rarefatto da poterlo considerare un gas ideale.
Tale scala termometrica, tuttavia, rimane legata alle proprietà dei gas perfetti, cioè di un particolare tipo di corpi termometrici. Onde sottrarsi a tali limitazioni, lord Kelvin15 definì una scala termodinamica delle temperature, basata sul secondo principio della termodinamica e pertanto indipendente dal particolare corpo termometrico utilizzato. Tale scala, per le assunzioni fatte, coincide numericamente con la scala assoluta delle temperature. I particolari delle considerazioni che conducono a tale definizione esulano dall’obiettivo di questo articolo e pertanto vengono omessi.
In conclusione, risulta che la definizione per classi della temperatura, a parte il necessario completamento delle operazioni strumentali che consentono di definire la scala termometrica, è in un certo senso essa stessa una definizione operativa, anche se le operazioni sono di natura mentale e non strumentale.
Infatti, il passaggio al quoziente che la caratterizza è un’operazione (non strumentale) nel senso moderno del termine, in quanto associa a ogni elemento di S uno e un solo elemento dell’insieme partizione S/R (operazione unaria non interna su S) secondo una legge ben determinata di natura sperimentale: la relazione di equilibrio termico.
Vai all’articolo in formato PDF
Luca Nicotra
(Ingegnere meccanico, giornalista pubblicista, Presidente dell’Associazione Arte e Scienza e Accademico Onorario dell’Accademia Piceno Aprutina dei Velati)
Note
Per le particolarità della temperatura come grandezza fisica si vedano: Piero Caldirola, Elementi di Fisica, vol.II, Milano Ghisetti&Corvi, p. 55, nota1; Eligio Perucca, Fisica generale e sperimentale, vol. I, Torino, UTET, 1937, p. 538; Ugo Bordoni, Fondamenti di Fisica Tecnica, vol. 1, Bologna, Zanichelli, 1970, pp. 173, 174.
La proprietà che varia al variare della temperatura e le cui variazioni consentono di ottenere una misura della temperatura è detta proprietà termometrica e caratterizza i diversi tipi di termometri (corpi termometrici): in quelli a gas a volume costante è la pressione, in quelli a gas a pressione costante è il volume, nei bolometri è la resistenza elettrica, nelle coppie termoelettriche è la forza elettromotrice, nei termometri a colonna liquida è l’altezza della colonna conseguente alla dilatazione termica, nei pirometri è l’irraggiamento, ecc.
Enrico Fermi, Fisica, vol. I, Bologna, Zanichelli, 1944, p. 141
Gaetano Castelfranchi, Fisica sperimentale e applicata, vol. I, Milano, Hoepli, 1943, p. 421
«…le varie grandezze fisiche […] sono sufficientemente definite e hanno esistenza reale in quanto si è d’accordo sul modo di misurarle» (E. Perucca, op. cit. p. 5).
Si dà per noto il concetto di calore, che non implica quello di temperatura, essendo il calore una forma di trasmissione dell’energia al pari del lavoro. Una parete (adiabatica o diatermica) impedisce i flussi di massa.
Pertanto, poiché nella misura della temperatura di un corpo il contatto termico fa evolvere verso una nuova configurazione di equilibrio gli stati termici sia del corpo in misura sia del termometro, è necessario che la presenza del termometro alteri il meno possibile lo stato termico iniziale del corpo. Ciò normalmente richiede che il termometro abbia massa molto piccola rispetto a quella del corpo in misura
L’opportunità di porre alla base della Termodinamica tale principio fu evidenziata fin dal 1871 dal grande fisico e matematico scozzese James Clark Maxwell e negli anni 1931, 1935 anche dagli astrofisici indiani M.N. Saha e B.N. Srivartava. Tuttavia, fu soltanto Ralph H. Fowler negli anni Trenta del Novecento a formularlo esplicitamente e a dargli il nome di Principio zero della Termodinamica in quanto logicamente precede i tre principi della Termodinamica, già formulati
L’ «o» in tal caso ha il significato alternativo (e non esclusivo) proprio della somma logica (per es. l’unione fra sistemi)
B. Russell, I principi della matematica, Roma, Newton Compton, 1971, p. 197
Per esempio, la relazione di equivalenza φ(a,b) = φ(a’,b’) ↔ ab’ = a’b (bb’ ≠ 0) che dovrebbe definire il concetto di frazione per astrazione non lo definisce in quanto la medesima relazione vale per la radice n-esima di un numero frazionario

Un gas si dice perfetto o ideale se le sue variabili di stato P (pressione), V (volume) e T (temperatura) soddisfano l’equazione PV = nRT, essendo la ostante R = Cp – Cv (Cp, Cv sono i calori specifici molari a pressione e a volume costante) ed n il numero di moli. I gas ideali sono approssimati in pratica dai gas reali a grandi rarefazioni
Con il termometro campione primario si misurano le temperature di un certo numero di stati scelti con accordi internazionali per il loro elevato grado di stabilità e riproducibilità (punti fissi della termometria), che sono utilizzati per la taratura di altri termometri campione secondari di più comodo utilizzo, i quali a loro volta sono utilizzati per la taratura dei termometri di lavoro, di utilizzo comune
Assunzione confermata nel 1990 con la scala internazionale delle temperature ITS90 (International Temperature Scale – 1990). Il punto triplo dell’acqua è lo stato in cui coesistono le tre fasi liquida, solida e aeriforme dell’acqua (in gradi Celsius la temperatura è 0,01 °C)
Lord William Thomson (1824 –1907) fu un fisico e ingegnere britannico nominato barone, con il titolo di lord Kelvin, per i suoi alti meriti scientifici.
© Pubblicato sul n° 52 di Emmeciquadro