Le teorie di Albert Einstein sono ancora considerate tra gli argomenti di Fisica di più difficile comprensione. Proprio per questo l’articolo che presentiamo può venire incontro all’esigenza di chi vuol accedere ai concetti della Relatività Ristretta o Speciale e della Relatività Generale.
L’esposizione che l’autore ne fa, a un livello di comprensibilità accessibile a chi abbia un certo patrimonio di conoscenze specifiche, offre la possibilità di seguire il percorso che ha portato Einstein alla formulazione delle sue teorie.
In particolare la lettura potrà essere utile a quei docenti che, soprattutto nell’ultimo anno dei licei, hanno la necessità di svolgere questo argomento.
Se da una parte le prime mosse dell’opera di Einstein partono dalla necessità di dare una spiegazione fisica al comportamento singolare della luce, evidenziato dall’esperimento di Albert A. Michelson (1851-1931) e Edward W. Morley (1838-1923), dall’altra, la struttura della Relatività Speciale acquista uno spessore possente non appena le invarianze che Einstein ottiene, vengono tradotte nella costanza dell’elemento della metrica spazio-temporale di Minkowsky.
Questo diviene, infatti, l’elemento chiave per l’aggancio della sua teoria alla più grandiosa architettura che la Fisica conosca per la descrizione della Natura, la Meccanica Analitica. Non appena tale elemento invariante viene inserito nel Principio variazionale di Hamilton, questo sarà in grado, effettivamente, di produrre risultati sorprendenti, completamente inaspettati per la dinamica, come la famosa equazione: E=mc².
Sarà solo il preludio della gigantesca costruzione della Relatività Generale, mediante la quale la teoria della gravitazione verrà tradotta in teoria geometrica dello spazio-tempo, spalancando alla formulazione newtoniana, un orizzonte di Bellezza e di profondità interpretativa inimmaginabile. Quando le equazioni di campo einsteiniane verranno innestate nella metrica cosmologica di Robertson-Walker, tutto il loro potere propulsivo della dinamica cosmologica trasparirà attraverso le equazioni di Aleksandr Friedmann (1888 –1925), base della cosmologia attuale.
Una frase sottende tutta la trattazione dell’opera scientifica di Einstein: «quello che c’è, nel mondo, di eternamente incomprensibile, è che esso sia comprensibile» [A.Einstein, 1936], vale a dire: c’è un ordine nella Natura recepibile dalle nostre categorie mentali!
Riprenderemo questa rilevante affermazione, alla fine della presentazione, quando tratteremo dei confini del dominio scientifico.
Teoria della Relatività Ristretta o Speciale: 1905 – annus mirabilis
L’intreccio spazio-tempo
La Relatività Speciale (RS) è basata su due principi base:
Principio di Relatività, che in seguito sarà esteso alla Relatività Generale (RG).
Principio di costanza della velocità della luce in due sistemi in moto relativo rettilineo e uniforme.
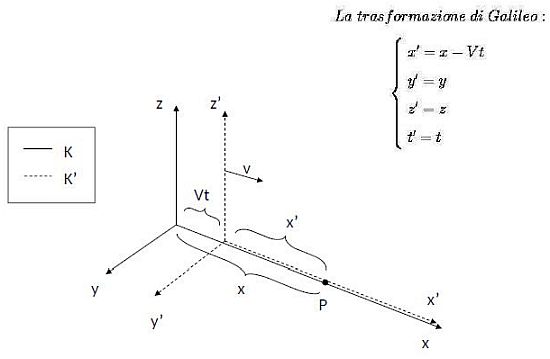Figura 1: Trasformazione di Galileo fra due sistemi di riferimento: K, fisso e K’, in moto traslatorio rettilineo e uniforme rispetto a K
Consideriamo la trasformazione di Galileo fra due sistemi di riferimento (Figura 1). Il sistema K è fisso mentre K’ trasla rispetto a K con moto traslatorio rettilineo uniforme, scivolando con il suo asse x’ lungo l’asse x.
Il Principio di Relatività afferma: «Le leggi fisiche valide in un sistema di riferimento K devono essere soddisfatte anche in ogni altro sistema di coordinate K’ che si muove di moto traslatorio rettilineo uniforme rispetto a K».
La sua conseguenza è che: nelle trasformazioni di Galileo, nel passare da K a K’, la dinamica rimane la stessa, vale a dire:
È da sottolineare come, nelle trasformazioni di Galileo, sia sottesa l’idea di Newton, vale a dire che lo spazio e il tempo sono assoluti. Questo quadro, come vedremo, si modifica nell’ambito della Relatività Ristretta e in quella Generale.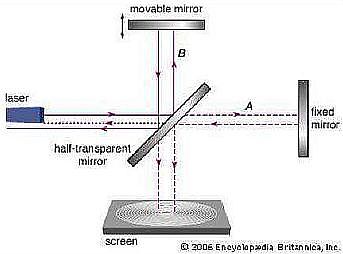
[Figura 2: Interferometro di Michelson – Morley]
Nel 1887, l’esperimento di Michelson – Morley mediante ‘uso dell’interferometro (Figura 2), aveva dimostrato che la figura d’interferenza (che appare nello screen) non cambia qualunque sia l’orientamento dell’interferometro rispetto alla velocità v di rivoluzione della Terra, come invece uno si aspetterebbe.
La velocità della luce c non si compone quindi con quella della Terra né con quella di alcun altro riferimento, rimane sempre: c = c0.
Non avveniva, quindi, quanto prospettato invece nella Figura 3.
Per spiegare questo comportamento, apparentemente paradossale della luce, Einstein era costretto a passare dalle trasformazioni di Galileo a quelle di Lorentz (Figura 5).
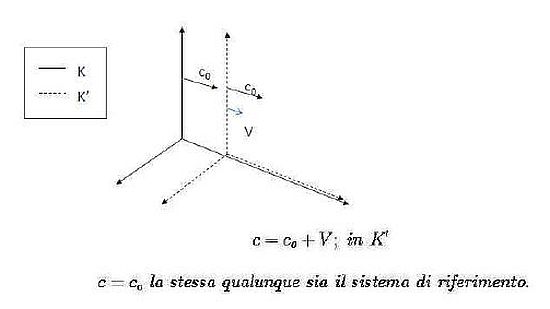Figura 3: Trasformazione di Galileo con sorgente luminosa, indicata dalla freccia, sia in K sia in K’. Ci si aspetterebbe che la velocità di propagazione della luce c0 si componesse, in K’, con la velocità v di traslazione del sistema di riferimento K’
La Natura quindi richiedeva, quando v si approssima a c, un inaspettato intreccio spazio-temporale, più precisamente:
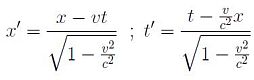
Dove la coordinata spaziale x compare nella trasformazione temporale di destra. Non appena v/c<<1, le trasformazioni di Lorentz ridiventano quelle di Galileo.
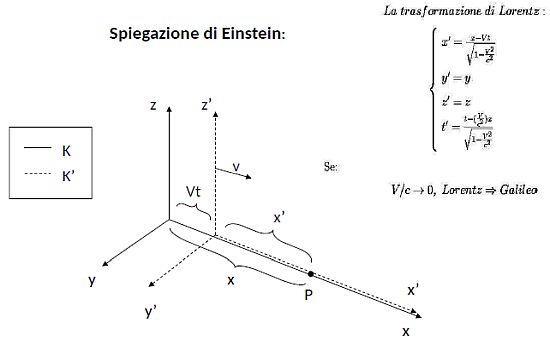Figura 4: Dalla trasformazione di Galileo a quella di Lorentz. La trasformazione di t → t’, coinvolge anche la coordinata x (quarta equazione)
L’intreccio introdotto, comporta tutta una serie di conseguenze apparentemente paradossali:
la contrazione della lunghezza L di un righello in movimento con il sistema K’, quando eseguita da un osservatore nel sistema K (contrazione di Lorentz); la dilatazione di un intervallo di tempo misurato in K’, rispetto allo stesso intervallo misurato dall’orologio nel sistema K (Figura 5).
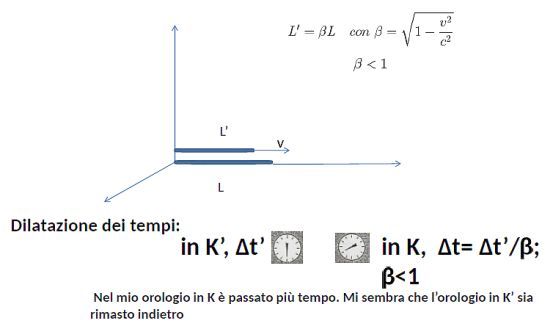Figura 5: Contrazione spaziale e dilatazione temporale per trasformazioni di Lorentz fra i due sistemi K e K’
La spiegazione di questi apparenti paradossi sta, sostanzialmente, nel problema della misura, che coinvolge la simultaneità delle osservazioni, ora divenuta relativa (Figura 6).
Infatti, due eventi simultanei nel sistema K, non lo sono più nel sistema K’, dato che le loro collocazioni spaziali (x₁, x₂) sono diverse ed altresì diversi risultano, quindi, i corrispondenti tempi (t’₁, t’₂) in K’.
Dalla trasformazione di Lorentz si ottiene infatti:
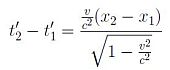
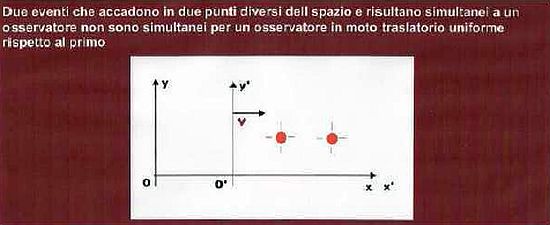
Figura 6: Relatività della simultaneità [si veda: Strumia, Relatività]
Sulla dilatazione del tempo
Nella Fisica delle particelle, esistono prove vistose sulla veridicità di tale dilatazione temporale nei fenomeni di decadimento, riguardante, per esempio il muone.
La sua vita media, di circa 2 μs, non gli permetterebbe di percorrere una distanza maggiore di circa 600 m prima di decadere. Non dovrebbe quindi essere possibile osservare tale particella nei raggi cosmici, che percorrono circa 15 Km di atmosfera, come invece succede.
L’altro fenomeno, non meno vistoso, anche se molto più complicato da verificare, coinvolgendo anche la RG, è il cosiddetto paradosso dei gemelli.
Un gemello viaggia alla velocità di 0.998 volte c verso una stazione spaziale a una distanza di 40 anni luce. Al ritorno, sulla Terra, l’intervallo di tempo trascorso è di circa 80 anni. Per l’astronauta l’intervallo di tempo è invece di circa 5 anni (Figura 7).
L’aspetto paradossale è non solo quello descritto, ma anche quello legato al possibile capovolgimento del punto di vista. Infatti, per il gemello astronauta è il gemello sulla Terra che è in moto, quindi a rimanere giovane dovrebbe essere quest’ultimo, mentre lui, l’astronauta, dovrebbe invecchiare.
Tenendo conto però che in RS i sistemi di riferimento a cui applicare la dilatazione temporale, devono essere inerziali, si conclude che non può esserlo quello dell’astronave, che nel suo tragitto deve subire delle accelerazioni sia all’inizio sia alla fine del viaggio.
L’analisi va quindi eseguita non solo mediante la RS ma anche la RG. L’esperimento, eseguito nel 1971 da J.G. Hafele e R. Keating [Hartle, 2003, p. 130, Cap.6], conferma le previsioni sia della RS che della RG.
Figura 7: Sulla dilatazione temporale: per il gemello che ha viaggiato il tempo è trascorso più lentamente [si veda: Fafone, 2001]
Lo spazio di Minkowsky
Seguendo l’insegnamento di Hermann Minkowsky (1864-1909), suo «maestro eccellente», Einstein introduce un sistema di riferimento pseudo-euclideo (a quattro dimensioni).
Il tempo rappresenta la quarta dimensione che si aggiunge alle tre dello spazio ordinario (Figura 8); data l’impossibilità rappresentativa di uno spazio a quattro dimensioni, ci limiteremo d’ora in poi, a solo due dimensioni spaziali (x, y) (immagine superiore) o anche a una (x) (immagine inferiore), dando per scontato che si sott’intendono le altre dimensioni spaziali mancanti.
In questo spazio, pseudo-euclideo, l’elemento infinitesimo della metrica, è dato da¹ (Figura 8, immagine inferiore):
(∆ s)²= -(c∆ t)²+(∆ x)²
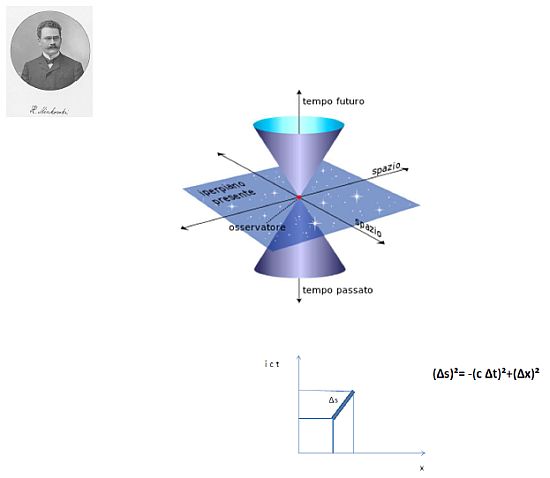Figura 8: Lo spazio di Minkowsky. Qui il tempo viene misurato lungo un asse temporale immaginario, «ict», essendo «i» l’unità immaginaria
Le conservazioni richieste dai due principi base (Principio di relatività e Principio di costanza della velocità della luce) diventano suscettibili, in questa metrica, di una interpretazione geometrica.
Le due invarianze si traducono, infatti, in invarianza dell’elemento spazio-temporale di Minkowsky, Δs, sotto trasformazioni di Lorentz:
In K, (∆ s)² = (c∆ t)² – (∆ x)² = (c∆ t’)² – (∆ x’)² = (∆ s’)², in K’
Da notare: il continuo spazio-tempo sembra conservi ancora qualche connotato di assolutezza, non per lo spazio, separato dal tempo, né per il tempo separato dallo spazio, come era per Newton, ma per una entità fatta in parte dall’uno e in parte dall’altro.
Vedremo come anche questa pseudo-assolutezza cadrà con la RG.
Conseguenze dell’invarianza di ∆s
È davvero sorprendente la ricaduta fisica che ha l’invarianza di ∆s. Non occorre fare nulla di più se non di introdurla in quel meraviglioso edificio costruito dai fisici-matematici, che è la Meccanica Analitica, base fondamentale per la descrizione fisica della Natura.
I pilastri di tale struttura sono i Principi variazionali, primo fra tutti quello di Hamilton (1805-1865). Non appena si costruisce il suo integrale variazionale per descrivere la dinamica di una particella libera, immediatamente tale Principio produce il lagrangiano e l’hamiltoniano relativistico che hanno in sé: il primo la capacità di far variare la massa con la velocità della particella, il secondo di mostrare una delle proprietà più affascinanti della Natura, vale a dire la relazione:
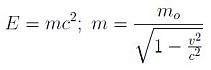dove m0 è la massa a riposo della particella.
Essa sancisce la conversione della massa in energia e viceversa con implicazioni enormi.
Conclusioni su RS
Riassumendo brevemente, i risultati salienti della RS sono: l’intreccio spazio-tempo, la contrazione dello spazio e la dilatazione del tempo (paradosso dei gemelli) per sistemi in movimento, la conversione Energia-Massa, tramite: E = mc².
La relatività della simultaneità: eventi simultanei nel sistema K non lo sono più in K’.
Diversamente da quanto a prima vista appare, la Relatività cerca, paradossalmente, di dare assolutezza a ciò che appare relativo, giungendo però alla fine a evidenziare una reale relatività dell’elemento spazio-temporale, con la RG, come vedremo.
Dalla Relatività Ristretta alla Relatività Generale
L’esigenza nasce non appena Einstein cerca di includere la teoria della gravitazione in RS. Ciò comporta, infatti, la presenza di accelerazioni.
Se ora K’ si muove di moto non più rettilineo e uniforme ma uniformemente accelerato rispetto a K, entrambi i sistemi, con ugual diritto devono poter essere scelti quali sistemi di riferimento per la descrizione dei fenomeni fisici coinvolti.
Deve valere il Principio di Relatività esteso: «Le leggi generali della Natura debbono potersi esprimere mediante equazioni che valgano per tutti i sistemi di coordinate, cioè (equazioni) che siano covarianti (in modo generale)² rispetto a qualunque sostituzione» [Einstein, 1916, pp.511-512].
Il concetto essenziale è che le coordinate non esistono a – priori in Natura, ma sono solo artifici usati nella sua descrizione e dunque non giocano nessun ruolo nella formulazione delle leggi fondamentali della Fisica.
Cronologia della Relatività Generale (RG) 1915, Novembre 25 1915, Dicembre 02 1916 |
L’idea geniale di Einstein
La prima idea, davvero geniale, di Einstein sarà quella di introdurre la gravità nell’elemento della metrica:
(Δs)² = c² (1+2Φ/c²) Δt² – (1-2Φ/c2 ) (Δx2 + Δy2 + Δz²)
Essendo φ il potenziale gravitazionale inserito sia nella parte temporale che in quella spaziale dell’ elemento infinitesimo dello spazio-tempo.
Einstein dirà: «…siamo capaci di “produrre” un campo gravitazionale semplicemente cambiando il sistema delle coordinate » [Einstein, Memoria del 1916].
Quali sistemi di coordinate?
In RS consideriamo lo spazio-tempo di Minkowski corrispondente alla Geometria di Euclide + tempo.
In RG consideriamo lo spazio-tempo di Riemann corrispondente alle Geometrie di Gauss + tempo. Le geometrie di Gauss includono anche quelle che violano il V Postulato di Euclide (Figura 9).
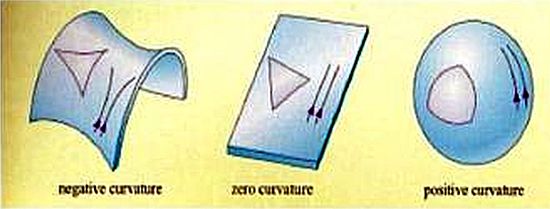Figura 9: Geometrie gaussiane: rispetto alla geometria euclidea, al centro, quando il piano diventa una sella (a sinistra), ci sono infinite «rette» (geodetiche) parallele a una data; viceversa, se il piano diventa la superficie di una sfera (a destra), le geodetiche diventano i cerchi massimi che si intersecano fra loro sempre, violando, di nuovo, il V Postulato di Euclide
In generale sono sistemi obliqui e curvilinei, con una particolarità: quella di essere localmente piatti (Figura 10).
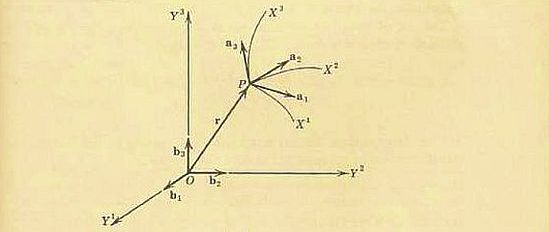
Figura 10: Sistemi di riferimento localmente piatti a causa dell’esistenza del Principio di Equivalenza. Nel punto P, quando Δs → 0, la geometria diventa quella euclidea
Alla domanda del perché essi debbano essere localmente piatti, la risposta sta nel Principio di Equivalenza a cui Einstein arrivò in modo piuttosto curioso. Sembra, infatti, che, mentre sedeva nel suo ufficio di Berna, abbia visto dalla finestra, un imbianchino cadere dal tetto di un palazzo nei pressi dell’Ufficio brevetti.
Il pensiero che gli attraversò la mente e che egli definì: «Il pensiero più felice della mia vita», fu il seguente: «Se una persona cade liberamente non sente il proprio peso». Se lasciasse cadere un oggetto, lo vedrebbe galleggiare accanto a sé, senza peso (Figura11 a).
Einstein raffinò il suo esperimento mentale (Gedankenexperiment) traducendolo nel seguente Principio: «Esperimenti in un laboratorio sufficientemente piccolo, in caduta libera, per un tempo sufficientemente breve, danno risultati indistinguibili da quelli degli stessi esperimenti in un sistema inerziale nello spazio vuoto». (Principio di Equivalenza).
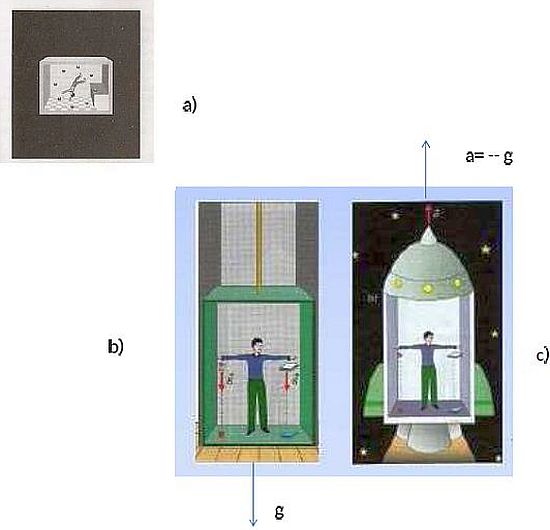Figura 11: Illustrazione del Principio di Equivalenza e delle sue conseguenze. Viene implicitamente assunta l’uguaglianza fra la massa inerziale e quella gravitazionale
Analogamente, per lo stesso Principio, un astronauta nel vuoto, quando la navicella viene accelerata con una accelerazione a uguale e contraria a quella gravitazionale g (Figura 11c), esperimenta gli stessi effetti come se si trovasse fermo sulla superficie della Terra (Figura 11b).
Facciamo notare che è implicita l’assunzione che la massa inerziale coincida con quella gravitazionale.
Conseguenze dell’inserimento della gravità nella metrica
Le conseguenze sono davvero notevoli.
La presenza di una massa modifica la metrica dello spazio-tempo (Figure 12 e 13).
Anche un fotone, in un campo curvato dalla gravitazione, flette la sua traiettoria (Figura 14).
Un qualunque corpo dotato di massa può quindi causare effetti di lente gravitazionale (Figura15).
Movimenti di masse causano increspature nello spazio-tempo che si possono propagare sotto forma di onde gravitazionali (Figura 16).
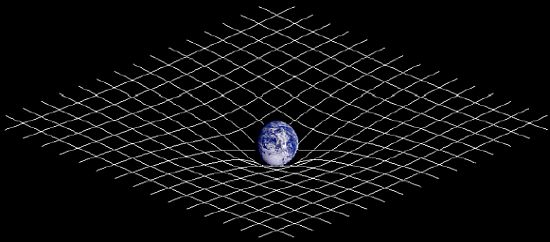Figura 12: La presenza di una massa comporta la deformazione dello spazio-tempo
La prima conseguenza comporta una vera e propria rivoluzione einsteiniana. Infatti, la forza newtoniana (Figura 13, in alto) non compare più in modo esplicito, al punto che la descrizione del moto, per esempio quello della Terra intorno al Sole, può essere fatta senza esplicito ricorso ad essa, ma semplicemente traducendo la presenza della forza di gravità fra due corpi, in distorsione dello spazio-tempo (Figura 13, in basso) .
Tale deformazione, dovuta al Sole, risulta allora la causa del moto orbitale del nostro pianeta attorno ad esso. La teoria della gravitazione di Newton, in questo modo, si trasforma in una teoria geometrica.
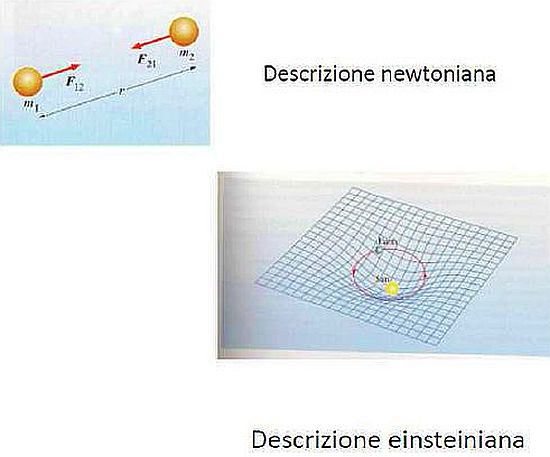Figura 13: Dalla descrizione di Newton (in alto) a quella di Einstein (in basso). La teoria della gravitazione diventa una teoria geometrica
Alla seconda conseguenza è legata la trionfale conferma da parte di Arthur Eddington (1882-1944), durante l’eclisse Solare del 1919, della nuova teoria gravitazionale di Einstein che ha avuto l’effetto di attirare su di essa l’attenzione generale.
In Figura 14, i punti in colore rappresentano le posizioni apparenti delle stelle, mentre i punti neri quelle reali causate dalla deflessione della luce da parte del campo gravitazionale del Sole che, al bordo, devia la luce di 1.75 arcsec.
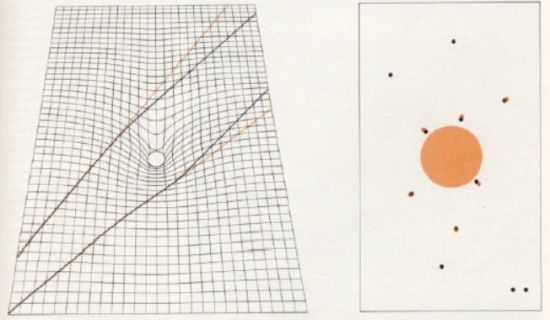Figura 14 (da V.Fafone, INFN, 2001): Anche la luce, in un campo gravitazionale che modifica lo spazio-tempo, flette la sua traiettoria. Le tracce in colore rispetto a quelle nere, a sinistra, danno un’idea del fenomeno, così come i punti in colore, a destra, descrivono gli effetti di tale deflessione durante l’eclisse solare del 1919
Un analogo fenomeno può anche essere prodotto, per esempio, da parte di un ammasso di galassie, in grado di deviare la luce proveniente da una galassia, quando esso si trovi interposto fra la galassia e la Terra (Figura 15).
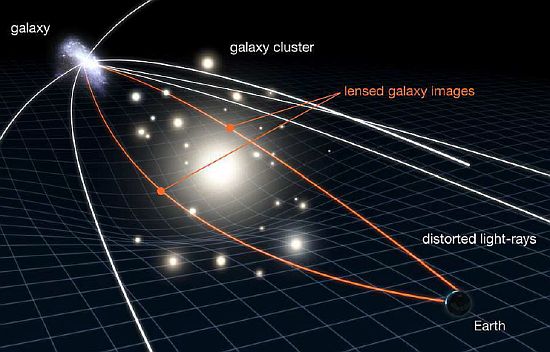Figura 15: Effetti di lente gravitazionale dovuti alla interposizione di un ammasso di galassie fra noi e una galassia oggetto di osservazione dalla Terra
Dedicheremo alle onde gravitazionali (Figura 16) l’intero, prossimo contributo.
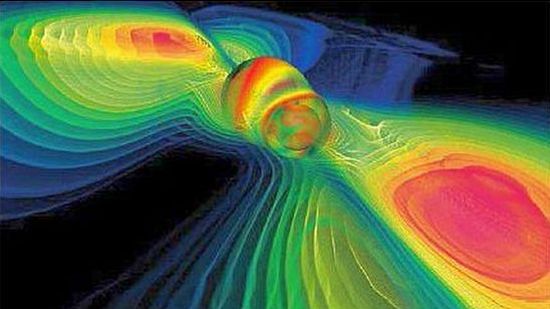Figura 16: I movimenti di masse, nel loro reciproco avvicinamento, causano vibrazioni dello spazio-tempo in grado di propagarsi come onde gravitazionali
Le equazioni del campo gravitazionale
Se l’aver introdotto il potenziale gravitazionale, φ, nell’elemento della metrica, era stata un’intuizione straordinaria, questo non esauriva, tuttavia, la ricerca di Einstein.
Si trattava, infatti, di completare il lavoro trovando il legame preciso fra un operatore di campo della gravitazione e le sue sorgenti, in analogia a quanto fatto da Maxwell per il campo elettromagnetico.
La ricerca delle equazioni del campo gravitazionale costituì una meta ardua per Einstein. Afflitto anche dalle proprie vicende familiari, nel periodo fra l’estate e autunno 1915, egli lotta per arrivare ad esse.
Vive solo, mangia e dorme quando capita, si consola con il violino (Figura 17) e viene sorretto dalle premurose attenzioni della cugina Elsa.
Figura 17: In attesa delle equazioni di campo
Il 25 novembre 1915, riuscirà finalmente a esporle nella quarta lezione del mese, all’Accademia prussiana delle Scienze. Riportiamo, solo per completezza, in Figura 18, la loro espressione formale, senza aggiungere alcuna specifica spiegazione, non adatta agli scopi del presente lavoro.
Cerchiamo invece di comprendere il loro senso e la loro enorme rilevanza dal punto di vista fisico.
Figura 18: Espressione formale delle Equazioni del campo gravitazionale, presentate da Einstein il 25 novembre 1915 all’Accademia prussiana delle Scienze [Strumia, Relatività]
Si tratta dell’uguaglianza di due operazionali, l’uno, , funzione della metrica spazio-temporale, l’altro, , funzione delle sorgenti gravitazionali:
(metrica spazio-tempo) = (sorgenti della gravitazione: materia + energia)
Tale equazione acquista un senso diverso se letta in un verso o nell’altro [Straneo, 1955].
Infatti quando questa relazione viene letta da sinistra verso destra ci dice: «è lo spazio-tempo che dice alla materia come muoversi»; letta invece da destra a sinistra: «è la materia + energia che dice allo spazio-tempo come piegarsi» (Figura 19).
Figura 19: Incurvamento dello spazio-tempo dovuto alla presenza di materia che, a sua volta obbliga una particella a muoversi di conseguenza [Strumia, Relatività]
Si passa così dalla ricerca iniziale di assolutezza di ciò che appare come relativo, all’evidenza che la Natura funziona invece così: «esiste un Principio di solidarietà fra i fenomeni e lo spazio-tempo, nel senso che ogni fenomeno si sceglie il proprio spazio-tempo. La conseguenza è la totale perdita, da parte dello spazio-tempo, di qualsiasi connotato di assolutezza».
Ulteriori conseguenze della RG
Elenchiamo qui semplicemente i nuovi capitoli aperti dalla RG, che potranno essere oggetto dettagliato di successivi contributi: cosmologia moderna e contemporanea; formazione di Buchi Neri (Black Holes), AGN, Quasar, Pulsar; onde gravitazionali; Effetto Lense-Thirring (satellite NASA Gravity Probe B, 2004); precessione del perielio di Mercurio.
Lasciamo piuttosto spazio per alcune considerazioni che esulano dall’ambito strettamente scientifico, per riferirci invece al terreno di confine fra Scienza e ciò che sta oltre il suo dominio, qui indicato, con un termine tipicamente aristotelico, come Metafisica.
I limiti della Scienza
Un qualsiasi scienziato li incontra non appena cerchi di rispondere alle domande «che cosa sono le grandezze fisiche? Che cosa è il tempo, lo spazio, la forza…?». Già S.Agostino (354-430 d.C.) affermava: «Che cosa è il tempo?….Se nessuno mi interroga, lo so; se volessi spiegarlo a chi mi interroga, io non lo so» .
Sappiamo dare definizioni operative per le grandezze fisiche, descrivendo, per esempio, la forza con gli effetti che essa produce oppure, declinandola, nel modo più moderno, mediante la teoria dei campi. Così l’interazione fra due cariche viene descritta attraverso lo scambio di mediatori, complice il Principio di Indeterminazione di Werner Karl Heisenberg (1901-1976) che fa da copertura a ciò che realmente avviene, senza nulla togliere alla consistenza fra l’interpretazione fisica e ciò che viene effettivamente osservato.
Heisenberg stesso si era espresso, dicendo: «Ci muoviamo sopra un grande abisso». Le grandezze di cui la Scienza si serve, sono intessute di qualche cosa che va oltre la Scienza.
Non ci si può occupare di Scienza senza avere la consapevolezza anche dei suoi limiti.
Essa ci appare allora come un terreno splendido da esplorare ma dotato di confini, come un’isola delimitata dall’oceano che la circonda (Figura 20).
Ed è proprio l’esistenza di questo oceano che lo scienziato non può dimenticare, rischiando, altrimenti, di smarrire il senso stesso della Scienza.
Figura 20: La Scienza come isola contornata dall’oceano di ciò che va oltre.
La «cifra» della Bellezza
Vi è un disagio da parte dello scienziato, un quid che lo inquieta: c’è, infatti, una «cifra indecifrabile» che, a priori, egli ha dovuto escludere dal suo dominio, perché non misurabile: la «cifra» della Bellezza.
Ma è proprio a partire da qui, nella transizione dalla quantità alla Bellezza –cifra della qualità-, che lo scienziato può trovare la chiave per aprirsi alla dimensione dell’oceano di cui prima, vale a dire alla Metafisica o alla Trascendenza, come suo sinonimo.
Concludendo la presente trattazione sull’eredità scientifica di Einstein, non mi sembra possibile non riprendere quel suo pensiero citato fin dall’inizio, che adombra il mistero della comprensibilità del mondo.
Ma se da una parte, ciò rende possibile la Scienza allo Scienziato, dall’altra, gli permette di sperimentare che «Quello che vedo nella Natura è una struttura stupenda che possiamo capire solo in maniera molto imperfetta» e quindi giungere a provare «un’umile ammirazione di quello Spirito immensamente superiore che si rivela in quel poco che noi, con il nostro intelletto debole e transitorio, possiamo comprendere della realtà». [Einstein, 1997].
Luigi Secco
(Dipartimento di Fisica e Astronomia, Università di Padova)
Note
Qui «Δ» viene considerato come infinitesimo. Ci sono due possibili convenzioni per il segno dell’elemento della metrica, che definisce il quadrato della distanza nello spazio-tempo: uno è quello indicato, e corrisponde alla parte inferiore della figura, l’altro è il suo opposto. Noi adotteremo, in seguito, quest’ultima convenzione adottata comunemente [Hartle, 2003, p.56].
Da intendersi, in questo contesto, come invarianti.
Indicazioni bibliografiche e sitografiche
Einstein, A., Memoria del 1916, in Cinquant’anni di Relatività, autori vari, p.511, Giuntine & Sansoni, Firenze 1955.
Einstein, A. , in The Journal of the Franklin Institute, Vol.221, n. 3,1936.
Einstein, A., in Pensieri di un uomo curioso, Mondadori , Segrate 1997.
Fafone, V., Teoria della relatività, 2001, INFN – www.Inf.infn.it/edu/slides/Fafone.pdf
Hartle, J.B., Gravity, an Introduction to Einstein’s General Relativity, Addison Wesley, 2003.
Straneo, P., in Cinquant’anni di Relatività, autori vari, p. 29, Giuntine & Sansoni, Firenze 1955.
Strumia, A., Relatività – www.albertostrumia.it/presentazioni/Relativita/Relativita.html
© Pubblicato sul n° 61 di Emmeciquadro
