Nell’esperienza didattica di Elena Aiolfi si manifesta una continuità da lei voluta per sottolineare e ampliare il significato dei calcoli, man mano che le situazioni evolvono.
Mentre i bambini approfondivano la conoscenza della loro regione, l’Emilia Romagna, interessandosi anche di un cibo caratteristico, le tigelle, la maestra ha fornito la ricetta per ventiquattro tigelle, che sono state confezionate, mangiate e offerte ad alcune insegnanti.
Ha poi variato il numero delle persone implicate, il che ha richiesto la divisione per otto e poi un passaggio moltiplicativo. Quindi è stato necessario operare con frazioni, introdurre misure decimali e dividere e moltiplicare numeri decimali: le operazioni sono state introdotte con un significato, e non solo come tecniche di calcolo.
Concreto e astratto sono condizioni ricche di sfumature, che descrivono il passaggio da una situazione problematica a una sua rappresentazione.
Nella scuola primaria, dopo aver imparato le operazioni tra numeri naturali, si deve passare a estenderle ai numeri decimali.
Qui si apre un nuovo capitolo dell’aritmetica, perché i decimali sono numeri razionali e cambiano le situazioni che danno significato alle operazioni. Cambiano inoltre alcune proprietà dell’ordine, che spesso i bambini lavorando con gli interi positivi, si sono abituati (erroneamente) a considerare universali. Ecco uno spunto per un laboratorio di matematica.
Comincia un nuovo anno scolastico: siamo in quinta! Non si può riprendere il lavoro di matematica con un generico ripasso di contenuti e regole. Raccogliamo l’occasione dello studio della regione Emilia Romagna: tra le tante particolarità, parliamo anche della cucina, e decidiamo di far sperimentare ai ragazzi la preparazione di un cibo tipico della zona di Reggio e Modena, le tigelle, piccoli panini rotondi che si mangiano ripieni di salame o di nutella.
In altre occasioni abbiamo sperimentato che un contesto «culinario» come la realizzazione di una ricetta è efficace dal punto di vista dell’apprendimento di molti concetti matematici, in particolare dell’introduzione delle frazioni, su cui si vuole lavorare in questo momento. Così, con grande interesse e coinvolgimento da parte degli alunni, ci siamo messi in azione, e in classe abbiamo impastato, atteso la lievitazione, cotto e mangiato le tigelle con tanto di salumi, formaggi e nutella.
Entra la matematica
Nella ricetta da cui siamo partiti, si davano gli ingredienti sufficienti per ottenere 24 tigelle: avendo deciso di darne tre a persona, sarebbero bastate solo per 8 bambini.
Ecco subito un problema da risolvere: le tigelle dovevano essere sufficienti per una trentina di persone, così si è deciso di farne per 32 persone, perché 32 è multiplo di 8; inoltre si sapeva che anche la preside voleva assaggiarle, e sembrava prudente farne in più – scelta rivelatasi molto opportuna quando sono passate ad assaggiarle altre insegnanti della scuola.
In questo modo, i bambini hanno subito calcolato che dovevano preparare 4 impasti con le dosi assegnate nella ricetta.
Mentre la pasta lievita, scriviamo gli ingredienti e il procedimento.
Tigelle cotte nella tigelliera
A questo punto, per riprendere il lavoro sulle frazioni e introdurre le operazioni con i decimali ho pensato di utilizzare l’esperienza iniziata al di là del contesto della conoscenza della nostra regione, proponendo nuove situazioni che portassero a lavorare sulla ricetta.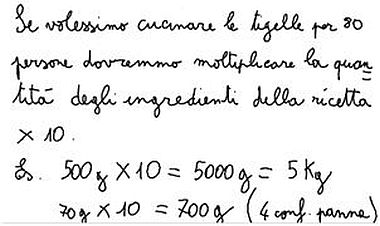 
Ho chiesto ai bambini di trovare gli ingredienti per preparare tigelle per 80 persone. Tutti hanno riconosciuto che bastava moltiplicare per 10 la quantità degli ingredienti della ricetta iniziale.
I bambini, anche quelli che presentano ancora difficoltà, hanno seguito bene, rifacendosi alle azioni concrete in cui tutti si erano coinvolti.
Per esempio, è stato interessante che, calcolando la quantità di panna necessaria, abbiano precisato il numero delle confezioni; hanno notato infatti che per l’impasto bastano 700g di panna, ma, trattandosi di confezioni da 200 g, si devono comunque prendere 4 confezioni, pur non utilizzando tutta la panna.
Occasione di nuovi apprendimenti
Fino a qui il cambio delle dosi ha richiesto solo di riconoscere una relazione di proporzionalità, lavorando con multipli interi di 8. 
Successivamente, ho chiesto di trovare gli ingredienti necessari per preparare le tigelle per 20 persone. Riferendosi alla ricetta di partenza, i bambini si sono sforzati dapprima di individuare un multiplo o sottomultiplo della quantità assegnata.
Dopo un lavoro di discussione e di prove di calcolo da parte di alcuni ragazzini, una di loro ha proposto: «Troviamo le quantità per fare le tigelle per una sola persona e poi moltiplichiamo per 20».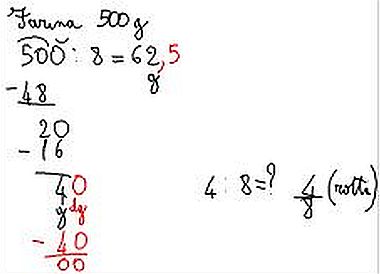 
Abbiamo osservato che questa idea era la migliore, perché in questo modo avremmo avuto un vantaggio: la ricetta si poteva modificare non solo per 20 persone, ma anche per qualunque altro numero desiderato di persone!
Allora abbiamo diviso per 8 la quantità in grammi di un ingrediente per volta, e si è presentata una situazione problematica: in ogni operazione rimaneva un resto, come considerarlo?
Ho fatto presente che «in cucina non si butta via niente», perciò saremmo dovuti andare oltre gli interi e avventurarci nei «rotti» (come già gli Egizi chiamavano le frazioni), suddividendo in 8 parti uguali anche quello che rimaneva per ciascun ingrediente.
Questa suddivisione è stata fatta associando a ciascun passo numerico la considerazione della marca che competeva alla cifra che si stava aggiungendo al quoziente, e queste considerazioni hanno permesso di dare ragione all’uso della virgola nella scrittura.
Per esempio, nel calcolo della quantità di panna, per poter proseguire nella divisione si poteva eseguire un’equivalenza nel resto, ma visto che si cambiava unità di misura, occorreva mettere nel risultato la virgola, per fare chiarezza e dire che si passava ai sottomultipli del grammo.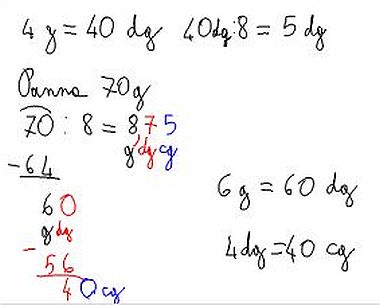
Come si vede nell’immagine a destra, se nel risultato fosse stato indicato 87, questi sarebbero dg (decigrammi) non g (grammi); oppure 875, sarebbero cg (centigrammi) e non g (grammi): occorre la virgola per chiarire che stiamo parlando di grammi.
Abbiamo osservato ancora che 4 g sono uguali a 40 dg e (40 dg : 8) sono 5 dg, perciò la virgola serve per separare l’unità di misura (grammo) dal suo sottomultiplo (decigrammo).
In questo modo abbiamo visto, partendo da una situazione reale, come gestire i decimali.
Così l’esperienza del «fare» le tigelle ha portato a rendersi ben conto dei rapporti tra le unità di misura, che decidono la posizione della virgola nell’eseguire una divisione tra due numeri che non sono tra loro divisibili, cioè due numeri che con il loro rapporto danno luogo a un numero razionale.
É stato poi possibile estendere le operazioni di divisione e moltiplicazione ai decimali lavorando all’interno di un problema, che assicurava un senso a queste operazioni. Infatti, tornando al problema di partenza, dopo aver diviso tutti gli ingredienti per 8, si è passati a moltiplicare per 20 quanto ottenuto.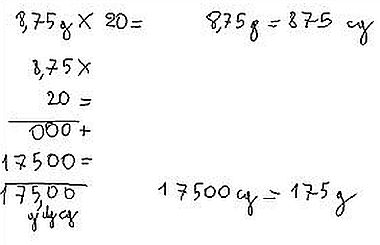 
Qui si è presentato un nuovo problema: come si moltiplica per un numero con la virgola? Nel nostro caso, dopo aver effettuato un’equivalenza, abbiamo moltiplicato 875 cg invece di 8,75 g; ma poi ci siamo dovuti ricordare che il risultato del prodotto è in cg (17.500), quindi, per avere di nuovo i grammi, occorreva un’altra equivalenza.
Con questi passaggi i ragazzi hanno capito la funzione della virgola nelle operazioni, che non avevamo mai fatto prima.
Nei mesi successivi c’è stato comunque bisogno di fare molto esercizio, ma la traccia del lavoro fatto emergeva continuamente, perché spesso mi bastava, davanti a un errore, richiamare: «vi ricordate delle tigelle? la virgola a cosa serviva?».
L’esperienza fatta è stata davvero paradigmatica: l’uso della virgola è risultato introdotto non come un meccanismo da applicare, ma come modalità di lettura della stessa quantità in diverse unità di misura, il che ha dato un senso alle regole del suo utilizzo, che gli alunni hanno capito e hanno usato con più coscienza, raggiungendo successivamente anche l’automatismo dei calcoli.
Il lavoro continua
Un contesto «ricco» non finisce di stimolare!
Abbiamo visualizzato in tabelle i risultati della divisione per 8 e della moltiplicazione per 20 e poi per 6 di ogni ingrediente, sia per dare l’idea delle quantità delle nuove ricette, sia per utilizzarle per un confronto e «leggerle» poi con il linguaggio delle frazioni.
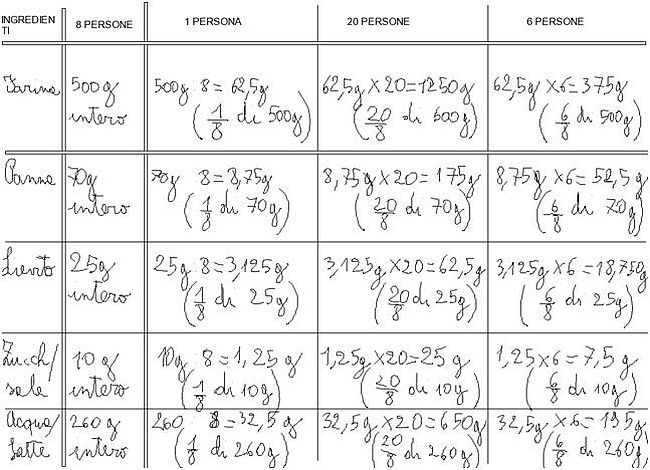
Dalla lettura di questa tabella emergono interessanti osservazioni riguardanti le frazioni.
Prendiamo per esempio la riga riguardante la farina.
500 g è l’intero, perciò se divido per 8, trovo 1/8 di 500 g, che è uguale a 62,5 g; moltiplicando per 20, trovo 20/8 di 500 g cioè 1250 g, una quantità superiore all’intero di partenza (due interi e mezzo). Se invece moltiplichiamo per 6, per avere le tigelle per 6 persone la quantità è inferiore all’intero, infatti 6/8 di 500 g sono 375 g.
Così abbiamo fatto una riflessione sulle frazioni minori o maggiori dell’intero: occorre osservare bene i numeri che esprimono una frazione. In seguito è stato più semplice per i ragazzi distinguere tra frazioni proprie, improprie e apparenti.
Una restituzione soddisfacente
In occasione dell’open day della scuola, i ragazzi hanno raccontato ai genitori, appoggiandosi a una presentazione fatta da loro, l’esperienza fatta e il percorso nella matematica.
Anche questa occasione ha permesso un importante passo avanti di consapevolezza personale da parte dei ragazzi: infatti, la verbalizzazione e narrazione della propria esperienza è altrettanto importante per l’apprendimento dell’esercizio di rinforzo dei procedimenti!
Anche se molti ritengono inutile richiedere che gli alunni cerchino e capiscano il perché delle cose, e si accontentano che sappiano eseguire e ripetere procedimenti correttamente, a me interessa sempre come prima cosa chiedermi «perché succede così?», e di conseguenza desidero che anche i ragazzi se lo chiedano.
Questo atteggiamento permette che avvenga il processo che chiamiamo «reinvenzione guidata», una strada di apprendimento e conoscenza ragionevole e umana, quindi anche efficace.
| Vai al PDF di questo articolo |
| Vai alla Home-Page della Rivista | Chi Siamo | Vai al Sommario del n° 69 – Giugno 2018 |
| Vai alla Sezione SCIENZ@SCUOLA | Vai agli SPECIALI della Rivista |
Elena Aiolfi
(Scuola Primaria Paritaria “Il Seme”, Castione Marchesi, Fidenza)
[Redazione a cura di Anna Paola Longo e Raffaella Manara]
Indicazioni Sitografiche
A. P. Longo, La dinamica Concreto/Astratto alla Scuola Primaria. Esperienze sul campo, in Emmeciquadro n° 47 – Dicembre 2012
A. P. Longo, Origine comune dei Decimali e delle Frazioni, in Emmeciquadro n° 52 – Marzo 2014
A. P. Longo, Esperienza e apprendimento. Una sinergia anche per la matematica, in Emmeciquadro n° 57 – Giugno 2015
R. Manara, Il laboratorio di matematica: in classe e oltre, in Emmeciquadro n° 59 – Dicembre 2015
© Pubblicato sul n° 69 di Emmeciquadro
