A distanza di 150 anni dalla pubblicazione del lavoro di Maxwell in cui compaiono le famose equazioni che reggono tutto l’elettromagnetismo e identificano la luce come onda elettromagnetica, l’autore riesamina la loro importanza e le loro conseguenze nello sviluppo della scienza. L’importanza teorica risiede nell’unificazione dei fenomeni elettrici e magnetici, quasi una profezia del tentativo di unificazione delle forze fondamentali, che da quasi un secolo è uno degli obiettivi, solo parzialmente riuscito, della Fisica. Ma anche nel collegamento con la nascita della relatività attraverso le trasformazioni di Lorentz. Infine anche i limiti di queste equazioni a livello dei fenomeni atomici hanno avuto conseguenze importanti, ma non hanno intaccato la loro validità nell’ambito dei fenomeni macroscopici.
Il 1865 è comunemente ritenuto l’anno di nascita dell’elettromagnetismo. In quell’anno infatti James Clerk Maxwell (1831-1879), 34-nne professore al King’s College di Londra, da cui però stava per ritirarsi, cominciò a lavorare al suo A treatise on Electricity and Magnetism.
La stesura occupò Maxwell per parecchi anni e il lavoro apparve solo nel 1873. Anche se questo lavoro potrebbe essere definito di tipo teorico, Maxwell seguiva con profondo interesse la sperimentazione, allora di punta, sui fenomeni elettrici e magnetici, in particolare quella di Michael Faraday (1791-1867). Maxwell stesso effettuò misure di carattere metrologico, essenziali per definire esattamente il peso da attribuire alle forze elettriche e magnetiche.
Quelli erano anni molto effervescenti dal punto di vista della ricerca su elettricità, magnetismo e ottica. Molti famosi scienziati, come Karl F. Gauss (1777-1855), André M. Ampère, (1775- 1836), Joseph J. Thomson (1856-1940) e il già citato Faraday vi erano coinvolti e avevano prodotto risultati fondamentali. Maxwell ebbe il merito di cogliere l’insieme di questi risultati e aggiungere ad essi quel di più che risultò determinante per concludere che campi elettrici e campi magnetici non erano grandezze separate, ma due aspetti inscindibili di un unico campo, il campo elettromagnetico.
Il sistema di equazioni creato da Maxwell era particolarmente bello e attraente, ma ciò non era sufficiente a decretarne l’importanza per l’avanzamento delle conoscenze fisiche. Perché ciò avvenisse si dovette attendere il 1885 quando il fisico tedesco Heinrich R. Hertz (1857-1894) dimostrò la possibilità di creare e rivelare le onde elettromagnetiche, previste da Maxwell e Faraday.
Anche con le sue limitazioni (la non invarianza per trasformazioni galileiane delle sue equazioni e l’incapacità di spiegare l’effetto fotoelettrico e lo spettro della radiazione di corpo nero) il sistema ideato da Maxwell si è rivelato importante, aprendo la strada all’introduzione, agli inizi del Novecento, della Relatività Ristretta e del concetto di fotone da parte di Albert Einstein (1879-1955) e Max Planck (1858-1947).
Le equazioni del campo elettromagnetico
Il campo elettromagnetico è completamente riassunto dal sistema delle equazioni di Maxwell (si veda la Scheda di Approfondimento n° 1), insieme di quattro equazioni che traducono quattro leggi fisiche ben note: la legge di Gauss per il campo elettrico, da cui aggiungendo la conservazione della carica e i principi di simmetria seguono tutte le proprietà del campo elettrostatico; la legge di Gauss per il campo magnetico da cui seguono tutte le proprietà della magnetostatica; la legge di Faraday-Neuman-Lenz che descrive la creazione di campi elettrici attraverso variazioni di campo magnetico; la legge della circuitazione di Ampère, che associa campi magnetici e correnti elettriche, modificata da Maxwell.
Prima della modifica da parte di Maxwell le quattro equazioni erano distinte e indipendenti. La legge di Faraday-Neuman-Lenz mostrava che da campi magnetici variabili derivavano forze elettromotrici e quindi campi elettrici, ma nessuno fino a Maxwell, incluso un fisico di vaglia come Faraday, era riuscito a mostrare l’inverso, benché ragioni di simmetria lo suggerissero fortemente.
Maxwell si rese però conto che questo insieme di equazioni violava la conservazione della carica e che per ristabilirla occorreva aggiungere al secondo membro della legge della circuitazione di Ampère il termine
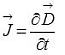avente le dimensioni di una densità di corrente. Nota come corrente di spostamento rappresenta per esempio l’effetto che si presenta tra le armature di un condensatore che si sta caricando o scaricando, necessario a ristabilire la continuità con la corrente ordinaria che scorre nei fili che alimentano il condensatore. Essa compare in qualsiasi mezzo, anche nel vuoto, ogni volta che in quel mezzo si verifica un variazione temporale del campo elettrico.
Con l’introduzione di questo termine viene ristabilita completa simmetria tra campo elettrico e campo magnetico e si spiega la comparsa delle onde elettromagnetiche.
Supponiamo infatti che in un punto dello spazio ci sia una carica che oscilla, allora in ogni punto dello spazio circostante compare un campo elettrico variabile. A causa di questa variabilità di 
e quindi di 
per la legge di Ampère modificata attorno a ognuno dei punti compare un campo 
.
Poiché anche è variabile per la legge di Faraday-Neuman-Lenz attorno a ogni punto in cui è apparso compare un campo variabile e il processo si ripete. Così a partire dalla carica oscillante partono campi elettrici e magnetici che si allontanano sempre più dalla carica.
Tutto ciò, espresso matematicamente, porta a scrivere due equazioni differenziali di secondo grado, una per e una per che si possono ottenere manipolando le quattro equazioni di Maxwell.
Ciascuna equazione descrive un’onda, una in e una in , il cui insieme è un’onda elettromagnetica (onda e.m.). Queste equazioni mostrano che entrambi i campi viaggiano anche nel vuoto e con una velocità molto elevata, pari a quella della luce nel mezzo in cui le onde sono immerse.
Le proprietà delle onde e.m. previste dalle equazioni di Maxwell (si vedano le Schede di Approfondimento n° 1 e n° 2), hanno trovato riscontro nelle osservazioni, validando il modello creato da Maxwell.
In particolare grazie al fatto che queste onde viaggiano anche nel vuoto, nel vuoto viaggiano alla velocità della luce, trasportano energia, subiscono effetti magneto-ottici (effetti Stark, Zeeman, Faraday, eccetera) identici a quelli che si verificano con la luce, come suggerito da Maxwell stesso, la luce è stata definitivamente classificata onda elettromagnetica (frequenza di circa 1015 Hz , lunghezza d’onda di alcune migliaia di Å) e si sono potuti sviluppare gli attuali mezzi di comunicazione e trasmissione dell’informazione.
Sono anche allo studio sistemi per trasmettere energia non via cavo, ma utilizzando onde e.m. di opportuna frequenza, copiando quanto già avviene in natura per esempio tra il Sole e la Terra.
Limiti delle Equazioni di Maxwell
Poco dopo la loro comparsa ci si rese conto che le equazioni di Maxwell non erano invarianti rispetto alle trasformazioni galileiane, abitualmente utilizzate per descrivere il passaggio da un sistema di riferimento a un altro in moto rettilineo uniforme rispetto al primo. 
In pratica ciò significava che le proprietà delle onde, per esempio il trasporto di energia, potevano essere radicalmente diverse se studiate da osservatori in moto rettilineo uniforme tra di loro, se si continuava a usare il cambio di coordinate fino ad allora utilizzato, quello descritto dalle trasformazioni galileiane. Era un problema grossissimo che metteva in crisi un assunto fondamentale della Fisica: le leggi fisiche devono essere scritte in modo da essere indipendenti dal moto dell’ osservatore.
[A sinistra: Hendrik Antoon Lorentz (1853 – 1928), scienziato danese, Premio Nobel per la Fisica nel 1902]
La fiducia sia in quest’ultimo assunto sia nelle equazioni di Maxwell era tale che ci si mise a cercare nuove trasformazioni che rendessero le equazioni di Maxwell invarianti. Imponendo l’invarianza furono così trovate le trasformazioni di Lorentz:
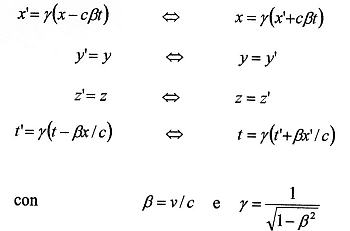dove si sono indicate con (x, y, z, t) le coordinate di un punto viste dal primo osservatore e con (x’, y’, z’, t’) le coordinate dello stesso punto viste dal secondo osservatore in moto rettilineo uniforme rispetto al primo con velocità v parallela agli assi x e x’.
Al momento si poté solo prendere atto del fatto che le equazioni di Maxwell erano invarianti rispetto a queste trasformazioni ancora misteriose, che avevano comunque il pregio di ridursi alle trasformazioni galileiane per valori di v piccoli rispetto a c, la velocità della luce nel vuoto.
Qualche anno dopo ci si rese conto anche che le equazioni di Maxwell non erano in grado di spiegare due effetti in cui erano indubitabilmente coinvolti segnali e.m. e cariche: l’effetto fotoelettrico e lo spettro della Radiazione di Corpo Nero. Era chiaro quindi che per quanto bello e interessante anche il modello del campo e.m. introdotto da Maxwell aveva dei limiti.
Le cause di questi limiti furono scoperte e i limiti aggirati grazie a Einstein e Planck con l’introduzione di tre ipotesi: la velocità della luce nel vuoto è una costante fondamentale della Fisica, il cui valore è indipendente dallo stato di moto o di quiete dell’osservatore; a livello atomico le energie che una particella legata può assumere formano un insieme discreto anziché continuo; in determinate condizioni la radiazione e.m. appare come insieme di particelle, i fotoni, a ciascuno dei quali è associata una energia hν (h costante di Planck, ν frequenza della radiazione). Da queste ipotesi sono nate la Relatività Ristretta e, dopo la scoperta del dualismo onda-particella, la Meccanica Quantistica.
Con lo scossone prodotto dalla scoperta dei suoi limiti l’elettromagnetismo di Maxwell ha definito meglio il suo ambito di applicazione (essenzialmente il mondo macroscopico) ed è ora noto come Elettromagnetismo Classico per distinguerlo dall’elettromagnetismo applicato prevalentemente a livello microscopico.
Equazioni di Maxwell e unificazione delle forze fondamentali
Prima che Maxwell presentasse le sue equazioni era convinzione dei fisici che tutti i fenomeni osservabili in natura fossero sostanzialmente riducibili a tre tipi di forze: forze gravitazionali, forze elettriche, forze magnetiche. Con la scoperta della radioattività e delle particelle alla base della struttura atomica e nucleare furono successivamente scoperte due altre forze fondamentali, la forza nucleare debole, responsabile del decadimento β , la forza nucleare forte, responsabile delle forze che legano i nucleoni all’interno dei nuclei atomici.
Con il suo modello Maxwell scoprì che le forze elettriche e quelle magnetiche sono due componenti di un unica forza, la forza e.m. e si separano solamente nei casi di campi stazionari, quando cioè le derivate rispetto al tempo che compaiono nelle equazioni di Maxwell (si veda la Scheda di Approfondimento n° 1) si annullano. Aveva realizzato la prima unificazione tra due forze fondamentali.
Poiché l’appetito vien mangiando i fisici cominciarono allora a pensare alla possibilità di unificare gradualmente tutte le forze fondamentali riducendole a un’unica forza. Einstein tentò di unire le forze gravitazionali a quelle elettromagnetiche senza riuscirci.
Tra gli anni Settanta e Ottanta del secolo scorso i fisici riuscirono invece a costruire un modello e a verificare sperimentalmente che a energie superiori a quelle tipiche del mondo in cui viviamo oggi, ma raggiungibili negli acceleratori di particelle, le forze elettromagnetiche e le forze nucleari deboli si unificavano; sono le forze elettrodeboli.
La speranza dei fisici è ora di arrivare a dimostrare che pur di salire ulteriormente con l’energia forze elettrodeboli e forze nucleari forti si uniscono in un’unica forza. A quest’ultima, a energie ancor più alte, dovrebbero unirsi infine le forze gravitazionali.
Conclusione
Dopo quanto abbiamo visto sopra è evidente che nel mondo relativamente freddo (di bassa energia) e macroscopico a cui siamo abituati e che cade sotto i nostri sensi, osserviamo soprattutto gli effetti delle forze elettromagnetiche. In altri termini le nostre azioni sono dominate dall’elettromagnetismo.
Come diceva un noto fisico italiano, Antonino Zichichi: «anche quando mangiamo un piatto di spaghetti noi facciamo dell’elettromagnetismo applicato».
Onore quindi a Maxwell a 150 anni dallo sviluppo organico del suo modello.
Vai all’intero articolo in formato PDF
Giorgio Sironi
(Università degli Studi di Milano-Bicocca)
© Pubblicato sul n° 53 di Emmeciquadro
