La spettroscopia ha una radice storica nell’osservazione della dispersione della luce da parte di Newton. Ma il vero inizio, come mette in evidenza l’autore dell’articolo, si ha con Joseph von Fraunhofer, inventore del reticolo di diffrazione e il primo ad analizzare, esattamente due secoli fa, nel 1814, lo spettro della luce solare. Di qui le applicazioni della spettroscopia, in primo luogo per l’identificazione degli elementi chimici.
All’inizio del Novecento l’analisi dello spettro dell’idrogeno, con le formule di Balmer e Rydberg ha dato origine all’ipotesi dei livelli energetici, inizio della meccanica quantistica dell’atomo. Infine, proprio dall’analisi spettroscopica della luce delle galassie è emerso il red shift, da cui la legge di Hubble, che descrive un Universo in espansione.
Nel 1655 l’università di Cambridge chiuse per due anni a causa dell’epidemia di peste1 e questo costrinse Newton a rimanere a casa; in quel periodo cominciò esaminare i concetti sulla teoria dei colori che portarono poi al suo famoso trattato di ottica, Opticks, pubblicato nel 1704. In una serie di esprimenti di rifrazione della luce tra il 1655 e il 1666 egli contraddisse la concezione, fino allora condivisa, che i fenomeni, come l’arcobaleno e il comportamento dei prismi, fossero dovuti a una modifica della luce prodotta dal mezzo, per esempio il prisma, e giunse ad affermare che la luce solare non è semplice e omogenea, ma una miscela di componenti più semplici: i colori dell’iride.
Arrivò quindi alla conclusione che passando attraverso un prisma triangolare i raggi dei diversi colori venivano rifratti con un angolo ben determinato, diverso per ogni colore.
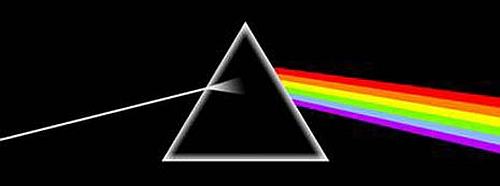Rappresentazione schematica della dispersione della luce da parte di un prisma
Questo costituisce l’inizio di quella che oggi si chiama spettroscopia, cioè l’analisi delle luce in base alla sua lunghezza d’onda, la proprietà che determina, per la luce visibile all’occhio umano, il colore2.
In realtà non esiste solo la luce visibile è ciò fu notato già dall’astronomo Frederick William Herschel (1738-1822) nel 1800: facendo scorrere un termometro lungo lo spettro si accorse che la temperatura saliva anche dopo aver passato il rosso in un una zona dove non si vedeva alcuna luce. Erano stati scoperti i raggi infrarossi.
Un anno dopo Johann Wilhelm Ritter (1776 -1810) scoprì i raggi ultravioletti ponendo del cloruro d’argento, che si sapeva scurirsi alla luce blu3, al di la del violetto.
Il contributo di Joseph von Fraunhofer: il reticolo di diffrazione
A questo punto conviene fare un salto di più di un secolo. Già Newton aveva utilizzato i suoi studi di diffrazione della luce per migliorare il telescopio; i telescopi galileani usavano le lenti ed era noto che queste, a causa di quella che si chiama l’aberrazione cromatica, dovuta alla rifrazione, producevano degli aloni colorati attorno agli oggetti osservati, per questo nel suo famoso telescopio4 passò a utilizzare degli specchi. Il problema della correzione dell’aberrazione cromatica aveva tormentato i costruttori di ottiche per decenni in laboriosi procedimenti di prove empiriche nell’accoppiamento di lenti di vetri diversi.
Joseph von Fraunhofer (1787-1826) che lavorava in una vetreria bavarese e si sforzava di migliorare il telescopio, si mise a studiare l’aberrazione cromatica con l’intento di avere un metodo sistematico e ripetibile di affrontare il problema.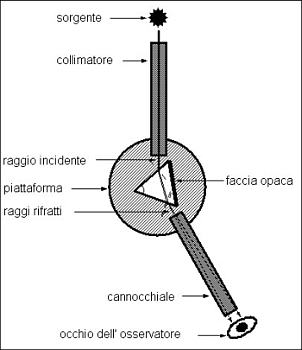
Si accorse che, per studiare le proprietà dei vetri, aveva bisogno di una luce monocromatica e andò a cercarla producendo fiamme colorate; avendo bisogno di un sorgente abbastanza intensa fissò l’attenzione su una riga giallo-arancio che era presente nello spettro di tutte le fiamme.
[A sinistra: Schema dello spettroscopio di Fraunhofer]
Dato che la luce solare era evidentemente la sorgente più intensa, a quel tempo, cercò la stessa riga nella luce del Sole e con sua grande sorpresa trovò un riga nera.
Un’analisi così accurata necessitava uno strumento di misura dell’angolo di rifrazione e quindi pose il prisma al centro di un teodolite, cioè un cannocchiale in grado di muoversi su un cerchio graduato. Inoltre perfezionò la fessura da frapporre tra la sorgente e il prisma osservando che questa avrebbe dovuto essere la più sottile possibile ma che la diffrazione poneva un limite alla riduzione della larghezza.
Questo dispositivo costituirà l’essenza di tutti gli spettrometri per molti decenni a venire.
Ormai Fraunhofer aveva uno strumento con cui poteva fare delle effettive misure confrontabili tra loro e nel 1814 si mise ad analizzare lo spettro solare individuando centinaia di altre righe scure. Le elencò in ordine alfabetico a partire dall’estremo rosso dello spettro per cui la famosa riga giallo arancio della fiamma assunse la lettera D.
Lampada stradale antinebbia ai vapori di sodio. La caratteristica luce gialla corrisponde alla riga D
Augustin-Jean Fresnel (1788-1827) in quegli anni pubblicò il suo lavoro sull’interpretazione matematica del fenomeno della diffrazione nel quadro della teoria ondulatoria della luce.
Fraunhofer si mise subito a studiare il modo di applicare la diffrazione alla formazione di spettri e costruì i primi reticoli di diffrazione.
I reticoli di diffrazione sono dei dispositivi costruiti in modo che la luce sia costretta a passare attraverso delle fenditure di larghezza costante a distanza altrettanto costante una dall’altra, la distanza e la larghezza devono esse comparabili con la lunghezza d’onda della luce.
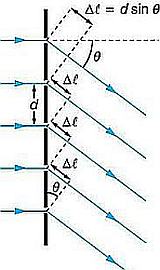
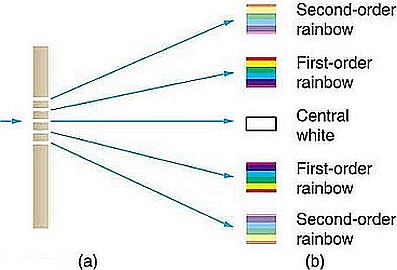
Schema di funzionamento di un reticolo di diffrazione.
A destra per un fascio monocromatico; a sinistra il fenomeno di separazione delle diverse lunghezze d’onda
Un esempio del fenomeno può essere dato dalla superficie di un CD in cui i solchi producono un serie di sottilissime superfici riflettenti con un comportamento assolutamente identico a quello delle fenditure.
Diffrazione della luce provocata dalla superficie di un CD; a destra un ingrandimento della sua superficie
Il primo reticolo fu costruito avvolgendo a distanze regolari un filo sottile attorno a un telaio, in seguito Fraunhofer, forte delle sue capacità nelle lavorazioni di precisione costruì diversi reticoli incidendo sottili solchi su una lastra di vetro ricoperta d’oro arrivando a una distanza di 0.0160 mm. tra un solco e l’altro.
Il grosso vantaggio che il reticolo aveva sul prisma era che lo spettro aveva una distribuzione uniforme nei vari colori e soprattutto, applicando le formule di Fresnel, era possibile risalire alle lunghezze d’onda dei singoli colori nota la distanza tra le fenditure:
Questa è la formula che lega la distanza tra le fenditure (d) alla lunghezza d’onda (λ) e all’angolo di deviazione (θm), misurato dal goniometro; m è un numero intero che indica l’ordine dello spettro (si veda l’immagine precedente).
In questo modo l’osservazione dello spettro diventava una misura quantitativa diretta in cui un numero, la lunghezza d’onda, poteva essere associato a ogni «colore», nello spettroscopio a prisma. Invece, l’angolo misurato dipendeva dalle proprietà dispersive del vetro utilizzato e questo rendeva difficile il confronto diretto delle misure tra strumenti diversi. Fraunhofer misurò la lunghezza d’onda della famosa riga D e ottenne 0.0005888 mm.
Nonostante l’indiscutibile vantaggio i reticoli di diffrazione, data la loro difficoltà di produzione, rimasero una rarità fino agli ultimi decenni del secolo, solo nel 1869 Anders Jonas Ångström (1814–1874)5 costruì il primo reticolo a riflessione che divenne di uso comune per la sua più semplice fabbricazione.
L’origine delle righe scure nello spettro della luce solare, anche se attribuite, in maniera abbastanza concorde da tutti, a un fenomeno di assorbimento, rimase a lungo un mistero.
Gli spettri degli elementi chimici
Quello che viene ricordato tra i primi ad aver associato un spettro agli elementi chimici fu Henry Fox Talbot (1800-1877)6 che analizzò lo spettro di una fiamma colorata da diversi composti chimici e fu forse il primo a supporre che lo spettro dipendeva dalla natura degli elementi introdotti. Un grosso limite a stabilire una correlazione tra elemento chimico e spettro era che la famosa riga D si presentava negli spettri di tutte le fiamme.
Il lavoro fu proseguito da William Swan (1818-1894) che si accorse che il problema era dato dal fatto che le sostanze introdotte nelle fiamma dovevano essere di eccezionale purezza, arrivò ad associare la riga D al sodio e determinò che pochi milligrammi di cloruro di sodio bastavano a colorare la fiamma. Lo studio fu pubblicato nel 1857 e si può dire abbia posto la prima pietra dell’analisi spettrale dei composti chimici.
Sul problema di correlare lo spettro alla natura chimica delle sostanze lavoravano anche Robert Bunsen (1811-1899) e Gustav Robert Kirchhoff (1824-1887) studiando lo spettro di fiamme luminose e scintille elettriche. Il lavoro di Swan aveva sottolineato la necessità di utilizzare sostanze ad elevata purezza, era quindi necessario che la fiamma non avesse di per sè un colore.
Bunsen sviluppò il bruciatore a gas che porta il suo nome e che è diventato quasi un simbolo del laboratorio chimico. Il vantaggio di tale apparato era che regolando il rapporto aria gas era possibile ottenere una fiamma ad alta temperatura e quasi incolore: l’alta temperatura favoriva la vaporizzazione della sostanza, la fiamma incolore non introduceva elementi spuri nello spettro.
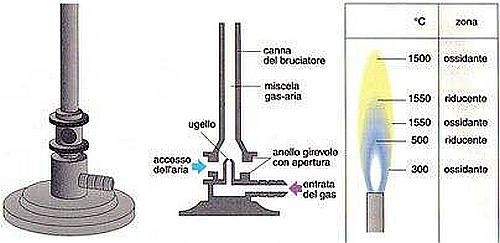Becco Bunsen. Al centro principio di funzionamento, a destra temperature della fiamma nelle diverse zone
I due giunsero alla conclusione che, posto nella fiamma, ciascun elemento metallico produceva una sua propria sequenza di righe spettrali e viceversa quando la luce bianca passa attraverso un vapore freddo si hanno nello spettro una sequenza di righe scure che corrispondono a quelle dello spettro di quel metallo quando era vaporizzato nella fiamma. In questo modo erano state poste le fondamenta delle due principali categorie di spettroscopia: quella di emissione e quella di assorbimento.
Si giunse all’enunciazione di quella che è detta legge di Kirkhoff: le righe dello spettro di emissione corrispondono alle righe nere dello spettro di assorbimento. Lo spettro di ciascun elemento è unico e identifica univocamente l’elemento; in questo modo la spettroscopia diventa uno strumento di analisi chimica.
Da notare che per la prima volta un metodo fisico diventa un metodo della pratica chimica per eccellenza: l’analisi elementare.
Il 20 ottobre 1859 Kirchhoff presentò all’Accademia di Berlino un lavoro sulle righe di Fraunhofer, che ormai era immediato collegare con gli elementi chimici presenti nel Sole, in cui forniva sia un’interpretazione chimica sia un accenno di spiegazione fisica.
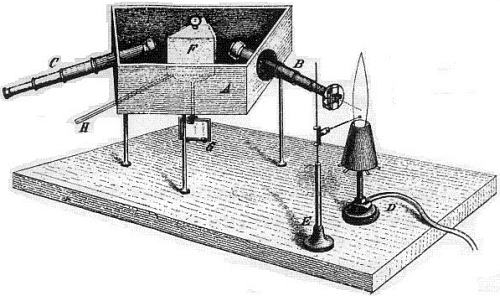Lo spettroscopio di Bunsen e Kirchoff
Ben presto la corrispondenza elemento chimico-spettro viene accettata dalla comunità scientifica e si passa a una sistematica raccolta dello spettro di tutti gli elementi conosciuti. Questo permette l’operazione inversa: uno spettro sconosciuto porta a prevedere un nuovo elemento.
Gli stessi Bunsen e Kirchoff già nel 1860 identificarono il cesio, che deve il suo nome proprio alle intense righe blu7 del suo spettro. Come molti elementi identificati spettroscopicamente il cesio fu isolato decenni dopo; il processo di riconoscimento di un nuovo elemento si è così invertito: l’elemento viene riconosciuto prima e non dopo averlo isolato. L’anno dopo, gli stessi identificarono il rubidio, che anch’esso deve il suo nome al colore delle righe principali del suo spettro, successivamente altri identificarono il tallio e l’indio.
Una sottolineatura particolare va data alla scoperta dell’elio; nel 1868, separatamente tra loro, due astronomi Pierre Janssen (1824-1907) e Joseph Norman Lockyer (1836-1920) attribuirono alcune righe, vicino alle righe D del sodio, a un elemento sconosciuto che fu chiamato elio; nel 1895 William Ramsay (1852-1916), che già aveva isolato l’argon, isolò un altro gas inerte che identificò spettroscopicamente con l’elio.
Quando all’inizio del Novecento Ernest Rutherford (1871-1937) e Frederick Soddy (1977-1956) dimostrarono che i raggi alfa erano formati da nuclei di elio la prova definitiva fu la coincidenza dello spettro: ormai era universalmente riconosciuto che lo spettro era come le «impronte digitali» di un elemento.
Lo spettro dell’idrogeno: le formula di Balmer e di Rydberg
L’uso di lastre fotografiche aveva nel frattempo migliorato la registrazione degli spettri; per prima cosa era possibile registrare anche emissioni molto deboli, bastava prolungare il tempo di esposizione, ed era possibile avere una stima oggettiva dell’intensità confrontando il grado di annerimento. Oltre a ciò l’emulsione fotografica registrava in modo eccellente l’ultravioletto che era invisibile all’osservazione diretta.
Quando si tentò di dare se non una spiegazione almeno un ordine alle righe dello spettro di un dato elemento, l’idrogeno attirò l’attenzione per la sua semplicità. Nell’immagine che segue è appariscente la differenza rispetto al ferro.
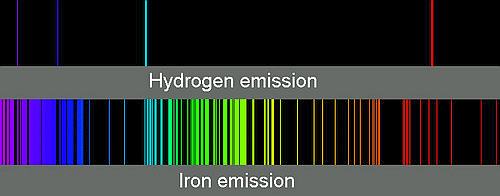Spettro di emissione dell’idrogeno (in alto) e del ferro (in basso)
Nel 1885 Johann J. Balmer (1825-1898) dimostra che le lunghezze d’onda nel visibile dello spettro dell’atomo di idrogeno possono soddisfare una semplice formula matematica:
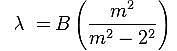dove B è una costante e m > 2 un numero intero.
Johannes Rydberg (1854–1919), tre anni dopo, generalizzò la formula di Balmer per tutte le righe dello spettro:
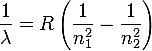dove R è la costante di Rydberg, n1 e n2 numeri interi, con n2 > n1; la costante R è una costante empirica e vale circa 1.097• 107 m-1.
Altre serie di righe furono scoperte da Friedrich Paschen (1865-947) nell’infrarosso nel 1908 e da Theodore Lyman (1874-1954) nell’ultravioletto nel 1906.
La formula di Rydberg continuava ad essere verificata, ovviamente con le opportune coppie di interi n per ogni riga: la serie di Lyman aveva n1=1, quella di Balmer n1=2 e quella di Paschen n1=3; in seguito furono trovate altre serie, con n1 maggiore ma la formula continuava ad essere verificata. Essa è ancora valida!
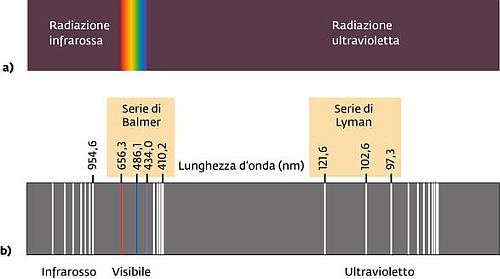Spettro completo dell’atomo di idrogeno
Dalla formula di Rydberg ai modelli atomici: i livelli energetici
Il risultato di Rydberg era indubbiamente un risultato brillante: un unica formula molto semplice prevedeva i risultati di una serie di esperimenti distinti; tuttavia non spiegava affatto la natura fisica dei fenomeni.
Era evidente che il fenomeno dell’emissione e dell’assorbimento della luce era di natura elettromagnetica e, a partire dalla scoperta dell’elettrone, da parte di Joseph John Thomson (1856-1940) nel 1898, divenne sempre più accettato che l’atomo fosse formato da particelle negative e positive e quindi in grado di interagire col campo elettromagnetico assorbendo ed emettendo energia, ma non era affatto chiaro perché questo avvenisse solo a lunghezze d’onda ben precise e per di più dipendenti da numeri interi.
Le equazioni di Maxwell, che governano tutti i fenomeni elettromagnetici, erano ormai un pilastro della fisica; esse sono equazioni continue le cui soluzioni danno necessariamente valori in grado di variare con continuità quindi non possono dare in nessun modo risultati nel discreto.
Tuttavia gli esperimenti davano in maniera inoppugnabile valori discreti e per di più una funzione di numeri interi li razionalizzava perfettamente: non era una spiegazione del fenomeno, ma comunque la formula era corretta.
La spiegazione era necessariamente legata alla struttura dell’atomo che nei decenni a cavallo tra Ottocento e Novecento stava perdendo la sua natura di particella indivisibile, ma mostrava sempre più una struttura interna complessa.
Alla scoperta dell’elettrone era seguita nel 1909, da parte di Rutherford, la scoperta del nucleo come sede di tutta la carica positiva e di conseguenza ne venne un modello planetario dell’atomo con il nucleo al centro e gli elettroni che gli girano attorno.
Il modello, cosa di cui era cosciente lo stesso Rutherford, era in contrasto con leggi fondamentali perché, proprio dalle equazioni di Maxwell, si ricava che gli elettroni in moto devono perdere energia elettromagnetica e quindi rallentare fino a cadere sul nucleo: un atomo di questo tipo non è stabile.
Nel 1913 Niels Bohr (1885-1962) presentò una descrizione dell’atomo d’idrogeno che riproduceva esattamente la formula di Rydberg per l’atomo d’idrogeno. L’ipotesi di partenza era che l’elettrone fosse vincolato ad avere valori ben determinati di energia e l’energia minima non era nulla, quindi percorreva circonferenze di raggio determinato, le orbite, come in un sistema planetario: non erano possibili situazioni intermedie, ovvero gli stati dinamici dell’elettrone erano «quantizzati».
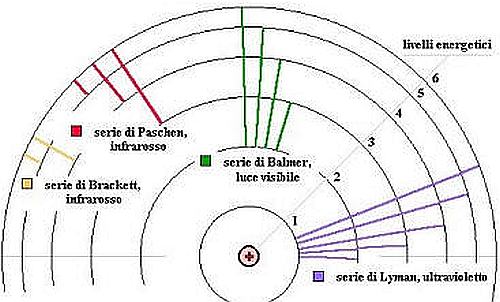Schema dell’atomo di Bohr con sovrapposte le transizioni, da un orbita all’altra, corrispondenti alle serie di Balmer, Lyman e Paschen. Notare come in ciascuna serie l’orbita più bassa abbia lo stesso numero e questo corrisponda a quello della formula di Rydberg
La quantizzazione dell’energia non era un’invenzione di Bohr, egli non aveva fatto altro che applicare al modello di atomo che conseguiva alla scoperta di Rutherford il principio che Max Planck (1858-1947) aveva pubblicato nel 1900.
Plank aveva elaborato un modello del corpo nero8, il cui comportamento non era spiegabile con la teoria classica dell’elettromagnetismo perché portava a risultati paradossali, introducendo l’ipotesi che gli atomi scambiassero energia in quantità proporzionali alla frequenza9 ν della radiazione elettromagnetica emessa o assorbita:
Dove h è la costante di Plank e vale 6.626 10-34 m2 kg / s.
L’idea di Plank poteva essere considerata solo un artificio gratuito almeno fino al 1905 quando Albert Einstein (1879-1955) spiegò l’effetto fotoelettrico, cioè l’emissione di elettroni da parte degli atomi per assorbimento di luce, utilizzando proprio la legge di Plank e ipotizzando che la luce avesse anche una natura corpuscolare. Nasceva così il concetto di fotone: un fotone di luce di frequenza ν possiede un’energia data dalla legge di Plank, non può essere assorbito od emesso se non un fotone intero. Il fotone è indivisibile e quindi è una particella elementare.
L’atomo di Bohr assembla questi due concetti: l’energia elettromagnetica scambiata nel passaggio da un stato all’altro non poteva variare in modo continuo ma con l’emissione o l’assorbimento di un fotone di frequenza corrispondente alla differenza di energia e i numeri interi della formula di Rydberg non erano altro che il numero ordinale dei vari stati, cioè il «numero quantico» degli stati elettronici.
La novità introdotta da Bohr è che l’energia degli stati elettronici negli atomi non può variare in modo continuo ma è quantizzata: questo spiega il fatto che gli spettri atomici sono formati da righe; la frequenza della riga corrisponde alla differenza di energia tra due stati secondo la legge di Plank.
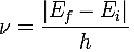E tenendo conto dell’equazione dinamica delle orbite
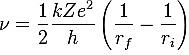i raggi delle orbite dovevano essere proporzionali ai quadrati di numeri interi per cui il momento angolare è:
Dove n sono gli interi della formula di Rydberg e h è la costante di Plank10.
Inoltre il modello di Bohr prevedeva un n energia per la prima orbita (n=1) di 13.6 eV che era in accordo con l’energia sperimentale di ionizzazione, cioè l’energia per estrarre un elettrone dall’atomo.
Dall’atomo di Bohr alla funzione d’onda di Schrödinger
A questo punto è necessario un nota bene. Il modello di Bohr, visto a un secolo di distanza, sembra un’ovvia applicazione dei lavori di Plank e di Einstein ma a quel tempo l’accettazione di quei risultati non era affatto pacifica; anche l’effettiva esistenza degli atomi era ancora ipotetica per alcuni11. E inoltre il fatto che in un certo anno viene pubblicata una teoria non vuol dire che questa venga conosciuta, capita e accettata da tutti: ci vuole un certo tempo.
La teoria atomica di Bohr si poggiava su un assunto, la quantizzazione degli stati elettronici, felice, perché rispettava i dati sperimentali, ma gratuito: bisognerà aspettare lo sviluppo della meccanica ondulatoria perché si possa avere una teoria fondata dell’insieme dei fenomeni atomici.
Nel 1926 Erwin Schrödinger (1887-1961) propose l’equazione che porta il suo nome e spiegava tutti i fenomeni allora conosciuti e anzi ne prevedeva di nuovi verificati in seguito.
Per l’atomo d’idrogeno l’equazione di Schrödinger è risolvibile analiticamente e riproduce lo spettro dell’atomo d’idrogeno; negli altri casi l’equazione è risolvibile solo numericamente, e quindi in modo approssimato, ma è comunque in grado di descrivere gli spettri degli atomi più pesanti dell’idrogeno, anche quelli che non rientrano nel modello di Bohr.
Siccome nell’equazione di Schrödinger si perde il concetto di traiettoria, quindi non si può più parlare di orbita dell’elettrone, ma si introduce il concetto di funzione d’onda12 associata alla particella, non si ha più un valore definito del raggio.
Il fatto che l’elettrone sia descritto da una funzione d’onda è in accordo con numerosi esperimenti in cui l’elettrone manifesta la sua natura ondulatoria come per esempio i fenomeni di diffrazione. Qui si ritorna al concetto di reticolo: nei solidi gli atomi sono disposti in modo periodico a distanze costanti, proprio come le fenditure del reticolo di Fraunhofer, e come quest’ultimo sono in grado di diffrangere un onda in questo caso l’elettrone. L’esperimento è stato effettivamente compiuto in modo positivo e anzi la diffrazione di elettroni è diventata un metodo di indagine dello stato solido.
L’interpretazione della funzione d’onda fu data da Max Born (1882-1970) che asserì che il suo quadrato dava la distribuzione di probabilità di trovare l’elettrone nello spazio e nel tempo. Questa interpretazione, anche se considerata insoddisfacente da molti fisici tra cui lo stesso Einstein, che tuttavia era stato uno dei principali fondatori della teoria quantistica, è ancora oggi comunemente accettata per i suoi riscontri sperimentali.
Dall’interpretazione probabilistica della funzione d’onda si ricava che la distanza media dell’elettrone dal nucleo nell’idrogeno, nei diversi stati, coincide con i raggi delle orbite di Bohr.
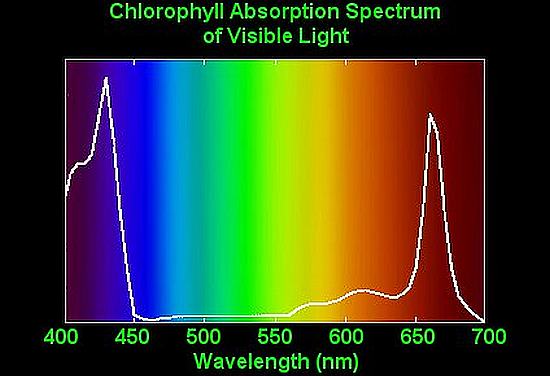Spettro nel visibile della clorofilla. I due picchi mostrano gli assorbimenti nel blu e nel rosso, la conseguenza è il colore verde della vegetazione
Osservazioni conclusive
In questa lunga carrellata ci si è limitati alla spettroscopia atomica che essendo legata solo al cambiamento di stato degli elettroni è ancora abbastanza semplice e quindi è stata il motore dello sviluppo della meccanica quantistica, che governa il comportamento delle particelle atomiche e subatomiche. Ma in parallelo a questa si è sviluppata anche la spettroscopia molecolare che anch’essa ha beneficiato della meccanica quantistica nella comprensione e previsione dei fenomeni. Questa è molto più complicata perché oltre allo stato dinamico degli elettroni bisogna tener conto di quello dei nuclei.
La spettroscopia molecolare ormai si è sviluppata in numerose spettroscopie che portano nomi diversi e utilizzano strumentazioni diverse ma tutte condividono i principi essenziali con i fatti raccontati; essa è essenziale per l’analisi chimica, lo studio delle strutture molecolari e, in questi ultimi tempi, con lo sviluppo di tecniche ultra veloci è anche possibile seguire l’evolversi in tempo reale di molte reazioni chimiche.
Infine dobbiamo ricordare l’importanza della spettroscopia in astrofisica, dove per esempio ha permesso di studiare la composizione chimica dei pianeti, e in cosmologia, dove attraverso il fenomeno del red shift ha evidenziato l’espansione dell’Universo (legge di Hubble).
Vai all’articolo in formato PDF
Emanuele Ortoleva
(Professore Associato di Chimica – Fisica presso l’Università degli Studi di Milano)
Note
Non si tratta di quella di cui parla Manzoni (1630) ma dell’epidemia successiva, solo venticinque anni dopo!
La lunghezza d’onda implica, intrinsecamente una teoria ondulatoria della luce: la luce è un campo elettromagnetico oscillante, cioè un campo elettrico ed uno magnetico associati, che si propaga nello spazio. Questa è la descrizione classica derivata dalla teoria unificata dei fenomeni elettrici e magnetici formalizzata da James Clerk Maxwell (1831-1879) con le sue equazioni.
Notare che siamo prima della scoperta ufficiale della fotografia (1827).
Il telescopio newtoniano è ancora uno degli schemi di costruzione dei telescopi ottici e anche dei radiotelescopi: è uno degli schemi più semplici.
Ångström studiò dettagliatamente lo spettro solare che pubblicò in unità di 10-10 m, unità molto utilizzata in spettroscopia che prende il nome di Ångström.
Fox Talbot è ricordato come pioniere delle fotografia in contesa con Daguerre, comunque fu l’inventore del primo processo negativo-positivo. In realtà fu un eclettico che si occupò anche di matematica e ottica.
Il nome deriva da caesius che in latino vuol dire blu cielo.
Il corpo nero è l’idealizzazione dei corpi reali che assorbono ed emettono luce per riscaldamento; un po’ come il gas perfetto è l’idealizzazione del comportamento dei gas reali.
Si ricorda che per la radiazione elettromagnetica frequenza e lunghezza d’onda sono legate da c = λ ν dove c è la velocità dalla luce.
La presenza di formule matematiche, a questo punto, è necessaria perché la teoria quantistica è essenzialmente una teoria matematica che porta risultati che riproducono i dati sperimentali e non un riassumere in forma matematica i risultati sperimentali.
La prova conclusiva dell’esistenza degli atomi e delle molecole fu data dagli esperimenti di Jean Baptiste Perrin (1870-1942) sul moto browniano nel 1908.
Per analogia con le orbite di Bohr si parla spesso di orbitali riferendosi alle funzioni d’onda: il termine è fuorviante perché nell’equazione di Schrödinger e in tutti gli sviluppi successivi della meccanica quantistica non si ha più niente di assimilabile a una traiettoria e quindi tantomeno a un’orbita.
© Pubblicato sul n° 53 di Emmeciquadro
