In realtà la trattazione teorica è molto complicata1 rispetto alle considerazioni fatte nel testo dell’articolo, basate solo sull’analogia, per certi aspetti, già in grado di giustificare l’esistenza delle onde gravitazionali.
La riportiamo per completezza, consigliandola solo a chi abbia una certa padronanza di questi argomenti.
Le onde nel vuoto
Si tratta innanzitutto di considerare le equazioni di Einstein del campo gravitazionale nel vuoto, vale a dire quando il tensore energia-impulso della materia:
![]() Esse si riducono al tensore di curvatura di Ricci,
Esse si riducono al tensore di curvatura di Ricci, ![]() che rappresenta 10 equazioni non lineari; linearizzare tali equazioni assumendo che il tensore metrico, nel generico punto2 dello spazio-tempo quadridimensionale, x:
che rappresenta 10 equazioni non lineari; linearizzare tali equazioni assumendo che il tensore metrico, nel generico punto2 dello spazio-tempo quadridimensionale, x:
![]() vale a dire sia dato dal tensore della metrica piatta di Minkowski,
vale a dire sia dato dal tensore della metrica piatta di Minkowski, ![]() = diag(-1,1,1,1), con l’aggiunta di un termine perturbativo legato all’onda gravitazionale, sufficientemente piccolo:
= diag(-1,1,1,1), con l’aggiunta di un termine perturbativo legato all’onda gravitazionale, sufficientemente piccolo: ![]() .
.
Operando poi una trasformazione di coordinate opportuna3, del tipo:
![]() dove le
dove le ![]() sono quattro funzioni arbitrarie tali che le derivate dei nuovi termini
sono quattro funzioni arbitrarie tali che le derivate dei nuovi termini ![]() , che ora nella formula
, che ora nella formula ![]() perturbano la metrica, soddisfino a determinate condizioni4, si trova che ciascuna componente perturbativa della metrica (lasciando cadere l’apice, per semplicità) soddisfa alla:
perturbano la metrica, soddisfino a determinate condizioni4, si trova che ciascuna componente perturbativa della metrica (lasciando cadere l’apice, per semplicità) soddisfa alla:
![]() che è l’equazione d’onda di d’Alembert per lo spazio piatto.
che è l’equazione d’onda di d’Alembert per lo spazio piatto.
Per un’onda con vettore d’onda, ![]() la soluzione dell’equazione di d’Alembert è:
la soluzione dell’equazione di d’Alembert è:
![]() essendo
essendo ![]() le ampiezze delle varie componenti dell’onda gravitazionale, corrispondenti alle varie componenti perturbative della metrica.
le ampiezze delle varie componenti dell’onda gravitazionale, corrispondenti alle varie componenti perturbative della metrica.
Orientando le coordinate spaziali in modo che l’asse «z» sia la direzione di propagazione dell’onda, si ottiene:
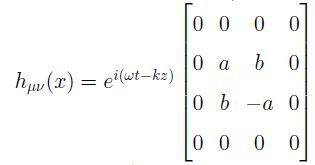 essendo
essendo ![]() , con il tensore
, con il tensore ![]() , in parentesi quadra, caratterizzato dall’avere le ampiezze lungo l’asse «z», tutte nulle (quarta riga) (azi=0, 0, 0 ; i=1,2,3$).
, in parentesi quadra, caratterizzato dall’avere le ampiezze lungo l’asse «z», tutte nulle (quarta riga) (azi=0, 0, 0 ; i=1,2,3$).
Si vede chiaramente che, dalle condizioni della gauge di Lorentz e dal fatto che il tensore, ![]() deve soddisfare all’equazione delle onde, la soluzione più generale delle Equazioni di Einstein linearizzate, ha la caratteristica di avere solo componenti trasversali all’asse di propagazione «z», vale a dire due componenti non nulle lungo «x» (seconda riga) (axi = a, b, 0) e lungo «y» (terza riga) (ayi = b, -a, 0).
deve soddisfare all’equazione delle onde, la soluzione più generale delle Equazioni di Einstein linearizzate, ha la caratteristica di avere solo componenti trasversali all’asse di propagazione «z», vale a dire due componenti non nulle lungo «x» (seconda riga) (axi = a, b, 0) e lungo «y» (terza riga) (ayi = b, -a, 0).
Il tensore ![]() risultante ha traccia nulla (Transverse Traceless (TT) gauge).
risultante ha traccia nulla (Transverse Traceless (TT) gauge).
Da notare che il processo di linearizzazione dota le onde gravitazionali di una proprietà di cui non godono invece le soluzioni delle equazioni originali di Einstein non lineari [Hartle, pag.333]: quella di potersi sommare dando luogo ad onde linearizzate che sono ancora soluzioni delle equazioni di Einstein in approssimazione lineare.
Le parti proporzionali ad «a» e «b» nel tensore di perturbazione della metrica, rappresentano i due diversi stati di polarizzazione dell’onda gravitazionale.
La prima è chiamata polarizzazione «+(plus)», la seconda «X (cross)». La soluzione generale è una sovrapposizione di onde con valori diversi della pulsazione, ω = 2π/λ c , diverse direzioni di propagazione e diverse ampiezze per i due tipi di polarizzazioni.
Le onde in presenza della materia
Quando il tensore energia-impulso ha componenti non nulle, non è possibile, in generale, esprimere, hμν (x) nella gauge TT. Possiamo frazionare la metrica in diversi pezzi, tuttavia solamente la parte esprimibile con la TT, obbedisce all’equazione di un’onda.
Espandendo le funzioni in termini di potenze di 1/r, si vede che, a grandi distanze, predomina ancora tale termine che rappresenta l’onda gravitazionale.
Più precisamente bisogna che, r >> Rsource, dove Rsource è la dimensione caratteristica della sorgente, e inoltre che λ >> Rsource.
La lunghezza tipica dell’onda gravitazionale, λ , è a sua volta data da: λ = c P, con il periodo P dato da, P = 2π/ω , essendo ω la velocità angolare con cui varia la sorgente.
Sui limiti adottati
È fondamentale notare che le considerazioni che vengono qui svolte, sia nel caso di vuoto che in presenza di materia, sono tutte soggette a tre limitazioni [Hartle, 2003, pag.510]:
Piccola curvatura ovunque nello spazio-tempo che permette l’uso di equazioni gravitazionali linearizzate;
Materia non in regime relativistico, cioè dominata dall’energia a riposo;
Velocità molto minori di quella della luce.
A queste limitazioni, certamente non obbedisce un fenomeno come quello che si ipotizza abbia generato le onde gravitazionali osservate, vale a dire la coalescenza di due buchi neri (Black Holes, BH).
Un tale evento richiede calcoli numerici molto accurati e relative simulazioni. Tuttavia l’approssimazione qui adottata, serve come guida di riferimento per il controllo di quanto numericamente viene poi sviluppato.
Luigi Secco
(Dipartimento di Fisica e Astronomia, Università di Padova)
Note
E’ richiesto un livello minimo specialistico.
Per semplicità si lasciano cadere gli indici μ.
Detta di gauge (=misura), in analogia con quelle usate per i potenziali del campo elettromagnetico
Dette condizioni della gauge di Lorentz [Hartle, pag. 463].
Nel nostro caso la gauge viene scelta in modo tale che le nuove variabili di perturbazione della metrica, descritte dal tensore, h’μν(x), abbiano la traccia, h’, del tensore rovesciata , rispetto a quella, h, del tensore iniziale (h’ = -h), da cui il nome: trace – reversed perturbation variables.
Nota Bibliografica
Hartle, J.B., Gravity, An Introduction to Einstein’s General Relativity, Addison Wesley Edition,2003.
© Pubblicato sul n° 62 di Emmeciquadro
