In questo contributo si dimostra, con alcuni dettagli, la confutazione newtoniana della teoria cartesiana dei vortici planetari, mediante la ricostruzione del ragionamento complessivo. Preliminarmente l’autore presenta la teoria dei vortici; successivamente sviluppa la trattazione fisico-matematica e infine conclude con alcune riflessioni personali. Un modo efficace di coniugare dimensione storica e dimensione concettuale e, nel contempo, un suggerimento di metodo e di contenuto per studenti degli ultimi anni di liceo.
Nel XVII secolo fu generalmente accolta, e insegnata nelle scuole, la teoria dei vortici di René Descartes come modello esplicativo dei moti planetari e satellitari del sistema solare. Se ne presentano di seguito i due punti fondamentali.
Lo spazio interplanetario è considerato un plenum, ossia è interamente occupato da materia disgregata. Ogni trasmissione di moto avviene per contatto, il movimento principale è circolare, trasmesso dal materiale fluido costituente i vortici stessi. I pianeti (e i satelliti) sono trasportati dalla materia fluida che gira costantemente attorno al Sole (e attorno al singolo pianeta): più rapide le parti vicine, più lente le parti lontane. I pianeti, Terra compresa, si comportano come un battello su un corso d’acqua trascinato dalla corrente.
Occorre poi ricordare, in senso lato, le vedute di Descartes per quanto riguardava i problemi fisici. Cartesio aveva scritto la «sua» fisica senza usare formule matematiche. Tutto ciò appare paradossale trattandosi di un filosofo-scienziato, profondo studioso di questioni algebriche e fondatore della geometria analitica, eppure è così.
La sua, è stato detto, era una fisica matematica senza matematica. Il principio fondamentale dell’universo cartesiano era quello di conservazione: tutte le azioni mutue meccaniche si riducevano alla legge della conservazione della quantità di moto. 
[A sinistra: René Descartes (1596-1650)]
Da questo punto di vista, e come indicazione degli intenti perseguiti nel costruire la fisica, è sintomatica una lettera scritta a padre Marin Mersenne (1588-1648) in data 15 novembre 1638 sul metodo galileiano, della quale riportiamo il seguente passo «Per ciò che scrive Galileo sulla bilancia e sulla leva, egli spiega molto bene il quod ita sit [che sia così], ma non il cur ita sit [perché sia così], come io ho fatto mediante il mio principio». 
Si può obiettare che nella fisica non si procede così: ossia non si pone un principio preminente su ogni altra considerazione di natura sperimentale.
[A destra: Isaac Newton (1642-1727)]
Come si pose Newton di fronte a questa teoria dei vortici?
Innanzitutto per lui le leggi della filosofia naturale (la fisica) erano scritte nei fenomeni stessi; occorreva poi indagare sensatamente, come diceva Galileo, per mezzo di un’appropriata analisi matematica e sperimentale. I successivi passi nello studio di Newton sono i seguenti: una disamina riguardante i fluidi viscosi e le loro proprietà; la traduzione in veste matematica della teoria qualitativa di Cartesio; la confutazione di quest’ultima, su una base che oggi diremmo popperiana, mediante il confronto con i dati sperimentali concernenti il moto dei pianeti e dei satelliti.
Generalità sui fluidi viscosi
Intitolata Moto circolare dei fluidi, la Sezione IX del secondo libro dei Principia sviluppa la teoria dei vortici circolari nei fluidi viscosi per dedurne interessanti proprietà.
Il testo newtoniano inizia così: «Ipotesi. La resistenza che nasce da una scarsa scorrevolezza delle parti di un fluido, a parità delle altre cose, è proporzionale alla velocità con la quale le parti del fluido vengono vicendevolmente separate». Per comprendere bene la portata di questa ipotesi è necessario aprire una parentesi di fluidodinamica delle correnti viscose. In qualunque buon testo [1] di tale disciplina si parla di correnti laminari.
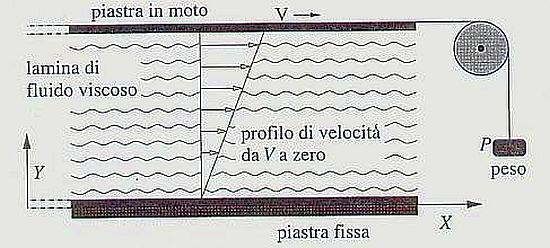Schema sperimentale per lo studio delle correnti viscose
Come appare nell’immagine, facciamo riferimento a due piastre metalliche parallele e sufficientemente lunghe contenenti, nel loro interno, un fluido viscoso. La piastra inferiore è stazionaria mentre quella superiore si muove con velocità v sotto l’influenza del peso P.
La forza che tira la piastra superiore deve essere controbilanciata da una forza uguale, ma in senso opposto, affinché v sia costante.
Questa forza, o meglio, lo sforzo di taglio T (forza per unità d’area) è dovuta al fatto che un fluido viscoso aderisca al solido contiguo. L’esperienza mostra che tale sforzo è lo stesso su tutti i piani paralleli alla piastra. Quindi a un’altezza qualsiasi y, lo sforzo di taglio T è espresso dalla formula
(1) 
Nella quale γ è il coefficiente di viscosità, A è l’area delle due superfici affacciate, F è la forza agente necessaria a separare le due superfici, Δy è la distanza tra le due superfici, Δv è la velocità relativa di una superficie rispetto all’altra.
Molto opportunamente i trattati di fluidodinamica ascrivono a Newton la legge espressa dalla (1). Infatti questa formula è nient’altro che la traduzione matematica della «ipotesi» di cui all’inizio del paragrafo. Conviene, nel seguito, applicare la (1) nel caso di due aree infinitesime dA, distanti dy e aventi velocità relative du sicché otterremo
(2) 
con 
Si noti nell’immagine il profilo di velocità u in funzione della y (risultato sperimentale) la cui pendenza è funzione della velocità v. Poiché du/dy è costante, ci ritroviamo T costante, come ipotizzato.
Sviluppo della confutazione newtoniana
Ricostruiamo il processo del pensiero newtoniano contenuto nella Proposizione LII del secondo libro dei Principia [2]. Vediamo come Newton applica i risultati ottenuti nel precedente paragrafo, adottando la viscosità γ costante per il fluido e mantenendo l’assunto cartesiano: la trasmissione, senza alterazione, e per contatto, di forze e coppie all’interno del fluido.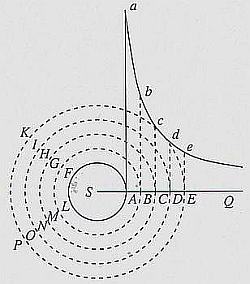 
L’inizio della Proposizione LII è: «Teorema XL. Se una sfera solida, in un fluido uniforme e infinito, ruota di moto uniforme intorno a un asse di posizione data, se il fluido è costretto a ruotare dal suo solo impulso, e se ogni parte del fluido persevererà uniformemente nel proprio moto: dico che i tempi periodici delle parti del fluido staranno come i quadrati delle distanze dal centro della sfera.»
[A sinistra: Correnti circolari in moto intorno alla sfera S]
Segue una dimostrazione di tipo qualitativo assai tortuosa e involuta, accompagnata dal diagramma riportato nell’immagine a sinistra.
In esso sono visibili i filetti circolari di fluido viscoso (la rappresentazione degli oggetti è in pianta) animati da velocità angolare ω (per esempio in senso diretto) attorno alla sfera S (che comunica il moto rotatorio) e decrescente monotonicamente con il raggio a partire da S, ossia tanto minore quanto più è grande il raggio del filetto stesso, come indicano le ordinate (a, b, c, d, e) del diagramma associato all’immagine. Questa distribuzione di ω secondo r è, peraltro, assai intuitiva. Ma Newton ricerca una dipendenza di ω da r in termini quantitativi, oggi diremmo ω = f(r).
Al termine della sua dimostrazione egli conclude: «Il tempo periodico dell’orbita qualsiasi DIO è, dunque, inversamente proporzionale all’area DdQ, cioè, per le note quadrature delle curve, direttamente proporzionale al quadrato della distanza SD. Il che ho voluto dimostrare come prima cosa.»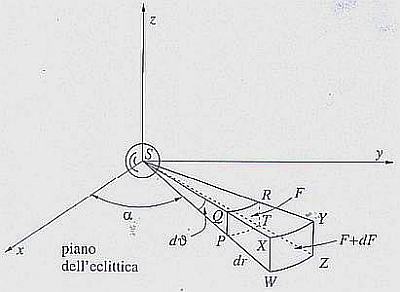 
[A destra: Elemento infinitesimo di corrente fluida sul piano dell’eclittica]
Riprendiamo la situazione prima detta con P sul piano equatoriale a distanza r dal centro di S, su un’orbita circolare come nell’immagine a destra. (a) Consideriamo un «parallelepipedo» infinitesimo PQRTXYZW con
PW = dr = QX = RY = TZ
A meno di infinitesimi di ordine superiore, e ugualmente
PQ = rdθ = RT = XW = YZ
E ancora
PT = rdα = WZ = XY = QR
Il parallelepipedo è soggetto alla forza di taglio dF tale che, per l’applicazione della formula (2),
(3) 
Essendo, a meno di infinitesimi di ordine superiore, rdω la velocità relativa della faccia PQRT rispetto alla faccia XYZW, poi r2dadθ l’area delle due facce (sempre a meno di infinitesimi di ordine superiore) e infine γ il coefficiente di viscosità. La formula (3) è la particolarizzazione della (2), del paragrafo precedente, nel caso in esame.
Conviene aprire una parentesi per spiegare l’espressione rdω che indica la velocità relativa tra le due facce opposte PQRT e XYZW. Passando da P a W, r diventa r + dr mentre ω diviene ω + dω. La velocità tangenziale, nel moto circolare in W è dunque (r + dr) (ω + dω), laddove in P è semplicemente ωr.
Pertanto la velocità relativa cercata sarà
(r + dr) (ω + dω) – ωr = ωdr + rdω + drdω
E, a meno di un infinitesimo di secondo ordine ωdr + rdω ora il termine ωdr non implica uno scorrimento tra le due facce (con relativo sforzo di taglio destato localmente) mentre ciò avviene per il termine rdω.
È quindi corretto, nel caso nostro, assumere du = rdω.
Ritorniamo alla deduzione riguardante ω(r)= f(r). Dalla (3) abbiamo
(4) 
Poiché γ è costante e dF dipende dal movimento rotatorio (coppia) impresso dalla sfera centrale S, ne risulta che la quantità dF/γdαdθ non dipende da r; essa è proporzionale alla forza impressa da S per unità di angolo solido.
La (4) si trasforma così
(5) 
Dove la quantità K è positiva e il segno «–» è dovuto al fatto che ω è decrescente con r.
La (5) pone a Newton un tipico problema della sua «teoria delle flussioni ». Infatti è ricercata la grandezza «fluente» ω = f(r), essendo stata assegnata la sua «flussione» dω/dr = φ (r).
Seguendo i trattati newtoniani Methodus fluxionum [3] e De Quadratura [4], la soluzione è immediata: la quantità fluente è
(6) 
proporzionale a 
Con P(r) il periodo di rivoluzione in funzione di r.
Oggigiorno questo è il problema della ricerca della «primitiva» di una data funzione φ(r) = dω/dr oppure, più semplicemente, un’integrazione rispetto a r. Ricordiamo la frase di Newton «Il tempo periodico dell’orbita qualsiasi […] per le note quadrature delle curve, è direttamente proporzionale al quadrato delle distanze [dal centro].»
Dopo aver posto la teoria di Cartesio in termini matematici, Newton passa al suo confronto con i dati sperimentali.
Infatti, nello scolio susseguente alla Proposizione LII, egli afferma: «In questa proposizione sono stato costretto a investigare le proprietà dei vortici, al fine di provare se i fenomeni celesti possano essere in qualche modo spiegati per mezzo dei vortici. Il fenomeno è il seguente: i tempi periodici dei pianeti che ruotano intorno a Giove sono nella relazione della potenza 3/2 delle loro distanze dal centro di Giove; la stessa legge si ottiene per i pianeti che ruotano attorno al Sole. Queste leggi, inoltre, valgono per entrambi i pianeti con la massima esattezza, in quanto discendono dalle attuali osservazioni astronomiche. Perciò se i pianeti che ruotano attorno a Giove o al Sole, sono trasportati dai vortici, anche questi vortici dovranno ruotare osservando la stessa legge».
Ecco quindi la chiave della verifica sperimentale: si confrontano i moti medi dedotti dalla teoria di Cartesio con quelli forniti dalla terza legge di Keplero. Quest’ultima è assunta come «base sperimentale» della verifica. Newton osserva che, per esempio, due satelliti di Giove, 1 e 2, compiono attorno al pianeta rivoluzioni tali che
(7) 
(terza legge di Keplero)
Essendo a1 e a2 i semiassi delle orbite dei satelliti con periodo P1 e P2.
A detti semiassi si possono sostituire, data l’assai piccola eccentricità dei satelliti gioviani,(b) le distanze costanti dal centro del pianeta.
Supponendo valida la teoria cartesiana si otterrebbe invece
(8) 
Con d1 e d2 le distanze dei satelliti dal centro di Giove.
Allora dal confronto tra il dato sperimentale
Con il dato previsto dalla teoria di Cartesio
Si conclude che la teoria di Descartes è falsa.
Che Newton annettesse grandissima importanza a detto risultato si evince dal fatto che egli lo cita esplicitamente nello scolio generale alla fine dei Principia, addirittura all’apertura. Ecco le sue parole: «L’ipotesi dei vortici è soggetta a molte difficoltà: perché un qualsiasi pianeta, condotto il raggio verso il Sole, descriva aree proporzionali ai tempi, i tempi periodici delle parti dei vortici dovrebbero essere in ragione del quadrato delle distanze dal Sole. Perché i tempi periodici dei pianeti siano nella proporzione della potenza 3/2 delle loro distanze dal Sole, i tempi periodici delle parti dei vortici dovrebbero essere proporzionali alla potenza 3/2 delle loro distanze. Perché i vortici minori possano conservare le loro rivoluzioni intorno a Saturno, Giove e agli altri pianeti e possano navigare liberamente nel vortice del Sole, i tempi periodici delle parti dei vortici solari dovrebbero essere uguali. Le rivoluzioni del Sole e dei pianeti intorno ai loro assi, le quali dovrebbero accordarsi con i moti dei vortici, discordano da tutte queste proporzioni. I moti delle comete sono sommamente regolari, osservano le medesime leggi dei moti dei pianeti, e non possono essere spiegati per mezzo dei vortici. Le comete sono trasportate con moti fortemente eccentrici in tutte le parti del cielo, il che non potrebbe essere fatto se non si eliminano i vortici.»
In questo passo è enunciata la confutazione della teoria cartesiana dei vortici. Scelta come paradigma, questa confutazione assurge però qui al livello di rigetto quasi totale della fisica cartesiana.
Newton non nascose il suo compiacimento per il suo risultato e, nello scolio alla fine del secondo libro, dichiarò: «Di qui è evidente che i pianeti non sono trasportati da vortici corporei […]. Per cui l’ipotesi dei vortici urta totalmente contro i fenomeni astronomici e conduce non tanto a spiegare quanto ad oscurare i moti celesti. In quale modo questi moti si effettuino negli spazi liberi indipendentemente dai vortici, può venir capito dal libro primo, e nel Sistema del mondo verrà insegnato più ampiamente.»(c)
Osservazioni conclusive
Contestualizzando questa ricerca nel suo tempo, i primi ottant’anni del secolo XVII, Newton perseguì due fini assai importanti per il progresso della scienza.
Innanzitutto continuò assai rigorosamente l’opera di Galileo considerando lo spazio, assimilato a un plenum, come un residuo della fisica aristotelica, assai resistente a essere giudicato per ciò che era, ossia un semplice pregiudizio. Certamente le critiche alla dinamica galileiana, e a quella dei suoi allievi, non si erano ancora così attenuate e quindi non erano completamente rientrate da poterle trascurare.
Se si legge un testo di storia della scienza che riflette gli orientamenti più diffusi nella seconda metà del XVII secolo [5] appare chiaramente quanto fosse allora radicata la convinzione che l’interazione meccanica tra corpi potesse avvenire solo per contatto: l’azione a distanza era considerata impossibile se non un’assurdità. Alle pagine 27 e 28 si può leggere: «Paolo Mattia Doria ricostruendo le vicende culturali che avevano contrassegnato la sua formazione ricordava che “tutti erano della filosofia di Pier Gassendi seguaci, né altro si cantava, che quel verso del poeta Lucrezio tangere, vel tangi nisi corpus nulla potest res”.
Era, si ricorderà proprio il punto sul quale si era accentrata l’attenzione del padre Vanni nella sua critica al Del Papa, ma era anche il punto che Leonardo di Capua riprendeva e sviluppava nel Parere, considerando uno dei pochi “sillogismi dimostrativi intorno alle cose naturali”, quello che riteneva “esser necessariamente corpo ciò, che gli organi de’ sentimenti ne muove; conciossiecosache la cosa, che muove, a ciò fare è ben mestier che tocchi; e ‘l toccamento, salvo che da corpo, non si può incontrare.» In secondo luogo la falsa teoria dei vortici cartesiani aveva conquistato larga parte dell’opinione scientifica più accreditata in Europa: bisognava sgombrare i cieli per poter procedere alla nuova interpretazione dei moti planetari.
Altre considerazioni interessanti riguardano il metodo di deduzione seguito in questa ricerca newtoniana. Lo scrivente è certo che Newton abbia condotto lo studio sino a impostare un’equazione differenziale del tipo della (5), per poi integrarlo più o meno come indicato nel paragrafo precedente. Ci si pone allora la domanda: perché allora egli non ha estesamente e palesemente esposto questo procedimento?
La risposta appare assai complessa: certamente vi è in Newton una certa ritrosia nel ricavare esplicitamente, e correlativamente esporre con i relativi dettagli, soluzioni giuste a partire da presmesse altrettanto giuste; in questo caso, peraltro, l’impiego di alcuni risultati, della sua opera Methodus fluxionum e Tractatus de Quadratura curvarum (entrambe scritte nel 1671 e quest’ultima citata fuggevolmente alla fine della Proposizione LII del secondo libro) ha fatto sì che egli evitasse, per correttezza, un’esplicita trattazione di tipo analitico completo. Infatti i citati due trattati furono regolarmente pubblicati postumi, mentre, ai tempi delle due prime edizioni dei Principia essi circolavano come manoscritti presso amici ed estimatori.
A conferma di queste tesi vi sono corrispondenze e manoscritti (presenti alla Royal Society) di David Gregory (1661- 1710) e altri presso la biblioteca Christ Churh di Oxford [6] che attestano come questo metodo di approccio, con equazioni differenziali, sia consapevolmente applicato in più parti dei Principia.
Oltre al presente argomento, occorre annoverare il corollario 3 alla Proposizione XLI del primo libro, la Sezione VIII del secondo libro, la Proposizione XXXV del secondo libro, la Proposizione XLIV del secondo libro e altri ancora.
In ogni caso è del tutto errata la netta affermazione di François de Gandt [7] secondo la quale non vi sarebbe stata alcuna applicazione, nei Principia, del calcolo infinitesimale, o meglio, flussionale di Newton. Il ragionamento fisico sui volumetti infinitesimi è, in questo caso, implicitamente condotto; in altri punti dei Principia del tutto manifesto: esso è comunque un tipico metodo di Newton.
Il grande matematico russo Vladimir I. Arnol’d nel suo testo edito da Bollati Boringhieri nel 1996 dal titolo Huygens, Barrow e Newton, Hooke, così si esprime a pagina 27: «Nei moderni corsi di analisi non è di moda parlare di grandezze infinitamente piccole, sicchè gli studenti non padroneggiano del tutto questo linguaggio; sarebbe bene tuttavia che se ne impadronissero».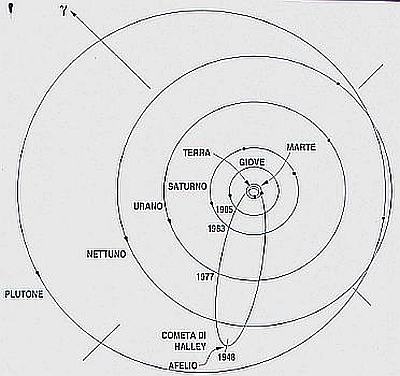
[A sinistra: Schema di rappresentazione in scala delle orbite planetarie e della cometa di Halley. Si osserva che dette orbite sono assai poco discoste dalla forma circolare con al centro il Sole. L’unica eccezione è Plutone. È riconoscibile la data dell’ultimo passaggio della cometa di Halley in vicinanza della Terra (1986). La sua orbita è inclinata di circa 18° rispetto al piano medio orbitale degli altri pianeti (Plutone escluso) ed è percorsa in senso retrogrado]
Per finire è interessante riportare alcuni passi del «Signor di Fontanelle», della Reale Accademia di Francia a proposito di questo nostro problema [8]. «Il Newton, com’è suo costume, stabilisce sovra una profondissima geometria ciò che deve risultare da quella resistenza [del mezzo o plenum interplanetario], secondo tutte le cause ch’essa aver puote: la densità del medio, la velocità del corpo mosso. La spaziosità della superficie. Et egli arriva infine a conclusioni delle quali vengono distrutti i turbiglioni o vortici del Descartes, e rovesciato quel vasto aereo edificio ch’altri credevano inconcussibile. Se i Pianeti si muovono intorno al Sole in un medio, qual egli sia, non ne resisterà meno, come vien dimostrato; in qaul maniera avverrà dunque che i movimenti dei Pianeti non ne siano perpetuamente,anzi, tosto, indeboliti? Sovratutto, come mai le comete traverserrann’elleno liberamente in ogni senso, quei vortici? […] I corpi celesti si muovono dunque in un grande vuoto, eccettuandone la poca materia che a spazi immateriali, e quasi infiniti, (o immisurabili) mescolata viene dalle loro esalazioni e raggi di luce che vi formano di se medesimi innumerabili intralciamenti. L’attrazione e il vacuo che Descartes esiliò dalla Fisica, e che allora secondo la apparenza, ne furono per sempre sbanditi; vi tornano ricondotti dal Newton, armati di una forza totalmente nuova […]».
Dopo aver letto questa vivace descrizione del 1757, possiamo concludere così: la visione newtoniana del mondo si impose dopo la metà del 1700 per la sua fecondità operativa e per l’ottima previsione dei moti planetari.
Vittorio Banfi
(Ha lavorato, dal 1969 al 1984, come collaboratore esterno presso l’Osservatorio di Pino Torinese. Membro del Centro di Astrodinamica «G. Colombo», ha sviluppato la sua ricerca nel campo dell’Astrofisica teorica del Sistema Solare)
Vai alla versione PDF di questo articolo
Note
- I Principia contengono le applicazioni del metodo del calcolo infinitesimale e integrale (a volte implicitamente a volte esplicitamente) che erano già maturate, negli scritti precedenti, a carattere matematico, di Newton. Le proposizioni presentate sono in grande misura quelle ottenute oggi dai metodi dell’Analisi Matematica, ma Newton li espose in forma di dimostrazioni sintetiche (libro secondo, lemma secondo), cui si ispira lo sviluppo analitico qui presentato
- Almeno quelli noti al tempo di Newton, ossia i satelliti medicei
- Il terzo libro dei Principia è detto anche Il sistema del mondo.
Indicazioni Bibliografiche
- D. Pnueli, Chaim Gutfinger, Fluids mechanics, Cambridge University Press, 1992
- Isaac Newton, Principi matematici della Filosofia naturale a cura di A. Pala., Utet, Torino 1965
- Isaac Newton, La methode des fluxions et des suites infinies, traduit par M. de Buffon, Librairie Scientifique et Tecnique A. Blanchard, Paris 1984
- Isaac Newton, Tractatus de Quadrature Curvarum, 1671
- Maurizio Torrini, Dopo Galileo una polemica scientifica, (1684-1711) Olschki, Firenze 1979
- Niccolò Guicciardini, Il dibattito sui metodi matematici per la filosofia naturale di Isaac Newton dal 1687 al 1736, Atti del XVIII Congresso di Storia della Fisica e dell’Astronomia
- François de Gandt, Le style mathematique des Principia de Newton, Rev. Hist. Sci. XXXIX/3, 1986
- Isaac Newton, La cronologia degli antichi regni emendate tradotti da P. Rolli (introduzione di Fontanelle), Editore G. Tevernin, Venezia 1757.
© Pubblicato sul n° 30 di Emmeciquadro
