In questo articolo si discute, a partire da esempi tratti da argomenti di matematica scolastica, il rapporto tra il progresso delle idee matematiche e lo sviluppo di certi linguaggi matematici specifici, e se ne trae qualche considerazione didattica (1). Viene qui pubblicata la prima parte dell’articolo, dove, partendo dalla scrittura dei numeri, si analizza il simbolismo dell’algebra e la sua estensione alla geometria con la geometria analitica.
Che cos’è il linguaggio? Lo strumento col quale comunichiamo un certo contenuto. Spesso si tende a contrapporre nettamente «linguaggio» e «contenuto», come se l’uno potesse prescindere dall’altro: quello che si dice in italiano si può tradurre in inglese (cambia il linguaggio, resta il contenuto), ciò che si dice in un linguaggio tecnico da addetti ai lavori può essere spiegato con un linguaggio divulgativo, alla portata di tutti. E così via.
Ma è proprio così? Una poesia scritta in una lingua può essere tradotta esattamente in un’altra lingua? La teoria della relatività può essere spiegata col linguaggio comune, senza usare i termini tecnici della fisica? Si può spiegare la matematica «in soldoni», senza usare i termini e i simboli matematici? Il contenuto è indipendente dal linguaggio col quale viene comunicato, o piuttosto necessita di un linguaggio adeguato ad esso? E il linguaggio aggiunge qualcosa al contenuto?
Un po’ di riflessione su questi problemi suggerisce che la relazione tra linguaggio e contenuto sia profonda e complessa.
Qui vogliamo affrontare il tema del ruolo del linguaggio in matematica. Per delimitare un po’ questo tema sconfinato, diciamo che non mi riferisco qui agli aspetti generali del linguaggio della matematica, che hanno a che fare con la logica, il modo di ragionare, o il modo di usare certe parole o espressioni del linguaggio comune che in matematica acquistano un significato univoco. Piuttosto, vorrei riflettere sull’apporto specifico che il linguaggio e il simbolismo danno a una specifica branca della matematica. Per questo motivo l’argomento di questa riflessione è meglio descritto dicendo che parliamo dei «linguaggi della matematica», al plurale.
Affronteremo questo tema attraverso alcuni esempi che mostrano come, da un punto di vista storico e logico, certi progressi del linguaggio matematico siano andati di pari passo con progressi nella comprensione delle idee. Gli esempi toccano argomenti di matematica scolastica, tuttavia le idee suggerite da questi esempi riguardano anche argomenti matematici più avanzati.
La scrittura dei numeri
Tutti noi abbiamo imparato da piccoli a sommare e moltiplicare due numeri interi «abbastanza grandi», mettendo i due numeri in colonna, e seguendo certe regole (sommare unità con unità, fare il riporto …). Come ben noto, ciò che rende possibile questo metodo è la scrittura posizionale in base dieci, cioè il fatto che il simbolo 132 denoti «un centinaio più tre decine più due unità», e le proprietà formali della somma e del prodotto. Per esempio:
132 +
46 =
178
Perché
132+46 = (1×100 + 3 x 10 + 2 x 1) + (4 x 10 + 6 x 1) =
(per le proprietà associativa e commutativa della somma)
= (1×100) + (3 x 10 + 4 x 10) + (2 x 1+ 6 x 1) =
(per la proprietà distributiva)
= (1×100) + (3 + 4) x 10 + (2 + 6) x 1 =
= 1×100 + 7 x 10 + 8 x 1 =
= 178.
I passaggi scritti sono la giustificazione formale del perché è lecito sommare unità con unità, decine con decine, e così via. Il fatto che la base scelta storicamente sia 10 non è essenziale (probabilmente dipende dal fatto che abbiamo 10 dita); il fatto realmente essenziale è la scrittura «posizionale», cioè in cui la stessa cifra ha un significato diverso a seconda della posizione che occupa, e ogni posizione individua una certa potenza di 10: primo posto = unità, secondo posto = decine, eccetera. Se, per confronto, proviamo a sommare 2 numeri scritti coi numeri romani, metterli in colonna non è di alcun aiuto:
CXXXII +
XLVI =
????
L’unica risorsa è usare un qualche tipo di abaco, per non perdere il conto!
Il sistema posizionale in base 10 entrò in occidente nel 1202, col Liber Abaci di Leonardo Pisano (1170-1250), che l’aveva conosciuto dagli arabi, i quali a loro volta l’avevano ricevuto dagli indiani intorno al 770, e avevano migliorato il sistema indiano aggiungendo lo zero, che gli indiani non usavano (lasciando al suo posto uno spazio vuoto). In India il sistema posizionale in base 10 era noto almeno dal 500, e qualcuno sostiene che fosse stato a sua volta importato dalla Cina, in tempi ancora più antichi.
Il linguaggio della scrittura posizionale in base 10 ha reso possibile l’esecuzione di calcoli numerici per iscritto, senza l’ausilio di abaco. Un progresso enorme non solo per la matematica, ma per la vita quotidiana di tutti.
Riflettiamo sul pensiero che ha reso possibile l’invenzione del sistema posizionale e la costruzione delle regole per eseguire le 4 operazioni per iscritto: occorre la consapevolezza delle proprietà formali della somma e del prodotto (commutativa, associativa, distributiva), l’idea di potenza (decine, centinaia, migliaia sono «potenze di dieci»), l’idea che ogni numero intero si possa rappresentare come somma di potenze di 10, dove tutti i coefficienti, a loro volta, sono numeri interi minori di 10, e quindi si possono rappresentare con le 10 cifre 0, 1, …, 9. Forse queste idee erano possedute da chi ha inventato il sistema in modo solo semi-esplicito, ma certamente senza una profonda riflessione sulle proprietà dei numeri e delle operazioni su di essi, questo linguaggio non avrebbe potuto essere inventato. La scrittura posizionale dei numeri ci appare allora, in questa luce, come molto più che «un buon espediente notazionale»: è una tappa importante nel cammino storico di riflessione sul numero e le sue proprietà, che viene definitivamente fissato in un linguaggio che diventa di uso comune, rende possibile calcoli di complessità potenzialmente qualsiasi, facilita ulteriori riflessioni sulle proprietà dei numeri (per fare solo un esempio elementare, si pensi ai criteri di divisibilità per 3, 5, 11, che si basano essenzialmente sulle proprietà della scrittura posizionale), ed è un presupposto per l’ulteriore estensione che consisterà nel considerare numeri con la virgola(2), rivoluzionando in ogni ambito sistemi e unità di misura. Infine, la scrittura posizionale dei numeri rappresenta, per noi che l’abbiamo acquisita, il modo stesso in cui «pensiamo» i numeri, quando sono «grandi»: possiamo infatti pensare e visualizzare il numero 5 in molti modi (5 puntini su un foglio di carta, le 5 dita di una mano…), ma non conosco che un solo modo per pensare il numero 754: come sequenza di cifre 7, 5, 4, col significato di 7 centinaia, 5 decine e 4 unità.
«Si fa molta fatica a pensare a qualche usanza universale che l’uomo abbia stabilito con successo sulla terra. Ce n’è una, tuttavia, di cui ci si può vantare: l’adozione universale dei numerali Indo-Arabi per scrivere i numeri. In questo abbiamo forse l’unico caso di vittoria mondiale di un’idea». (Howard W. Eves (1911-2004)) (3)
Il linguaggio dell’algebra
Uno dei primi e più elementari problemi di cui l’algebra si è occupata è la risoluzione delle equazioni algebriche di primo e secondo grado. Col linguaggio attuale, si tratta delle equazioni del tipo:
Ax + b = 0 (primo grado)
Ax2 + bx + c = 0 (secondo grado)
Dove x è l’incognita e a, b, c sono coefficienti assegnati. Per l’equazione di primo grado, per esempio, la soluzione è:![]()
(purché sia a ≠ 0). Questo modo di formulare i problemi è detto dell’«algebra simbolica», ed è una conquista del XVI secolo, per arrivare alla quale è stato necessario un lungo e faticoso cammino del pensiero matematico. Qui non vogliamo tracciare un resoconto storico di questi sviluppi, ma solo segnalare due punti-chiave di questo progresso.
Il primo, che si può far coincidere con l’invenzione stessa dell’algebra, è il concetto di «equazione in un’incognita». Anzitutto l’idea di «incognita», cioè l’idea di dare un nome a una quantità che ancora non conosciamo (e neppure sappiamo se esista) ma che, se esiste, deve soddisfare una certa uguaglianza. Successivamente, su questa uguaglianza contenente un’incognita (= equazione) possiamo eseguire determinate operazioni che trasformano l’uguaglianza in un’altra equivalente ma sempre più semplice, fino ad arrivare alla soluzione, se esiste.
Esemplifichiamo su un problema tratto dal già citato Liber Abaci di Leonardo Pisano (4).
«Dice un giovane: “Oggi, se al triplo della mia età aggiungo 1/4 e 1/3 di quanto ho già vissuto, mi manca solo un anno per avere 100 anni”. Qual è l’esatta età del giovane in anni, mesi e giorni?»
Possiamo formalizzare il problema introducendo un’incognita: x = età del giovane, e quindi traducendo l’informazione contenuta nel testo in un’equazione:![]()
Su questa equazione si può ora operare, prima trasformando l’espressione a primo membro come
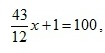
Quindi sottraendo ad ambo i membri dell’equazione 1 e successivamente moltiplicando ambo i membri dell’equazione per 12/43, ottenendo:
![]()
Tutte le operazioni effettuate sono lecite in base alle proprietà generali della somma e del prodotto dei numeri reali.
Questo modo di procedere per noi è naturale e quasi banale, ma occorre riflettere sul grado di astrazione implicito in questo ragionamento, e consistente anzitutto nell’uso del concetto di «incognita» e di «equazione», e quindi nell’utilizzo corretto delle proprietà delle operazioni anche quando queste coinvolgono un «numero incognito». Senza queste idee, il problema andrebbe risolto con un ragionamento certamente più tortuoso. In realtà Leonardo Pisano risolve questo problema senza usare esplicitamente il metodo risolutivo dell’equazione di primo grado, ma col «metodo di falsa posizione»; in generale Leonardo, che pure conosce le equazioni, ne riserva l’uso a problemi formulati in modo più intricato di questo. In sostanza, però, il suo ragionamento utilizza sia il concetto di incognita che quello di equazione (espressa a parole); solo nei passaggi risolutivi si discosta dal nostro metodo e si rifà piuttosto alle proporzioni (che comunque sono particolari equazioni). Tradotto in linguaggio simbolico infatti, il suo ragionamento verbale è il seguente:
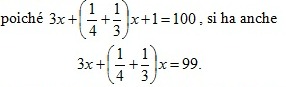
Se fosse x = 12 («falsa posizione») il primo membro risulterebbe 43 invece che 99 (si noti che, grazie alla scelta astuta del numero 12, questo è un calcolo facile da fare «a mente»: la forza del metodo è questa). Dunque vale la proporzione
![]()
Anche se abbiamo usato il linguaggio simbolico moderno per fare un resoconto del ragionamento di Leonardo, si noti che di per sé l’idea di equazione in un’incognita è indipendente dall’uso di un particolare formalismo. Storicamente l’algebra nasce nell’alto medio evo, presso gli arabi, come «algebra retorica», dove l’incognita è chiamata «la cosa» e tanto l’equazione quanto il suo procedimento risolutivo sono interamente raccontati a parole (da cui appunto il nome di algebra retorica). La risoluzione per questa via è molto faticosa (6), e c’è voluta immaginazione e lungimiranza, da parte dei matematici medievali e del primo rinascimento, per pensare che questo metodo algebrico avrebbe potuto dare dei buoni frutti, se ben coltivato.
Il secondo punto chiave in questo sviluppo, infatti, consiste appunto nel passaggio dall’algebra retorica all’algebra simbolica. Questo passaggio, lungo e graduale, ha un’interessante anticipazione intorno al 1200 con l’opera di Giordano Nemorario, che rimane però isolata, subisce un’accelerazione con gli algebristi italiani del rinascimento, che iniziano a usare ciascuno le proprie abbreviazioni simboliche (si parla di «algebra sincopata» per descrivere questo stadio di sviluppo), e si considera avere un punto di svolta decisiva intorno al 1600 con la figura di François Viète (1540-1603) (7).
L’algebra simbolica a sua volta è caratterizzata da due innovazioni cruciali: la prima è l’uso di un «simbolismo standard» per scrivere le equazioni (anziché doverle raccontare a parole), che rende celere e trasparente il procedimento risolutivo; la seconda è l’uso di «coefficienti generici», cioè l’idea di dare dei nomi (per esempio a, b, c) ai numeri (considerati noti, non incogniti!) che compaiono nell’equazione, al fine di poter risolvere «in un colpo solo» tutte le equazioni di un certo tipo, e non solo una specifica equazione.
Per esempio, se vogliamo mostrare come si risolve la generica equazione di primo grado, è sufficiente scrivere
Ax + b = 0
Con a, b generici numeri reali. Sottraendo b ad ambo i membri e quindi dividendo per a ambo i membri (se a ≠ 0), si trova la soluzione generale:
![]()
Prima della nascita dell’algebra simbolica, i trattati di algebra insegnavano a risolvere le equazioni unicamente attraverso esempi numerici, senza la possibilità di enunciare simbolicamente una regola generale: non esisteva un linguaggio capace di questa generalità.
L’uso di lettere per denotare coefficienti generici si intreccia con un altro problema, che è l’uso dei numeri negativi, pienamente affermatosi in Europa solo nel XVI secolo (con Rafael Bombelli (1526-1572), Simon Stevin (1548–1620). Per chi non conosce i numeri negativi, le equazioni
Ax2 + bx = c; ax2 = bx + c; ax2 + c = bx
Non sono tre casi particolari dell’equazione generale
Ax2 + bx + c = 0,
Ma piuttosto tre classi di equazioni ben distinte. È il fatto di considerare anche la possibilità che a, b, c indichino numeri negativi che unifica i tre «casi» in uno solo.
Sintetizziamo.
Il linguaggio dell’algebra simbolica utilizza lettere per denotare incognite e coefficienti generici. Questo procedimento rende celere la formalizzazione e risoluzione di molti problemi, e consente di formulare sinteticamente le regole generali di risoluzione.
Tutto ciò è strettamente connesso a certi progressi fatti nell’evoluzione del pensiero matematico.
L’affermarsi di un certo tipo di ragionamento astratto: dare un nome ad una ipotetica quantità che ancora non conosciamo, ma che, se esiste, deve soddisfare una certa uguaglianza, e trarre conseguenze opportune da questa uguaglianza.
L’idea di scrivere e risolvere le equazioni in simboli, non a parole.
L’idea che si possano stabilire relazioni valide per numeri qualsiasi indicando questi con delle lettere (parametri). Quest’idea è naturalmente intrecciata a un approfondirsi della consapevolezza delle proprietà astratte delle operazioni di somma e prodotto di numeri: per scrivere
A(x + 1) = ax + a
Occorre avere chiara la proprietà distributiva, e aver capito che proprio la generalità con cui vale quella proprietà ci consente di affermare che è lecito scrivere uguaglianze letterali: queste uguaglianze «non ci tradiranno» quando sostituiremo a una lettera un numero concreto, proprio perché le proprietà che applichiamo sono valide per ciascun numero. Ma allora si può usare sistematicamente lettere al posto di numeri e stabilire formule di valore generale.
Il concetto di «numero negativo» (e non solo di «sottrazione di un numero da un altro»), che consente di unificare procedimenti che altrimenti si frammenterebbero in una casistica complicata.
L’esempio dell’algebra mostra quindi come il linguaggio matematico non sia semplicemente un modo per «comunicare» certe idee, ma sia esso stesso il luogo in cui «risiedono» certe idee. Il linguaggio incorpora in sé progressi, idee, giudizi, astrazioni frutto di una lunga storia. Per questo quando ragioniamo usando un certo linguaggio, certi problemi (non tutti!) appaiono banali, mostrano da sé la strada per la propria soluzione. In realtà il problema non può essere considerato banale di per sé; piuttosto, si può dire che in quel caso il linguaggio si sia fatto carico della maggior parte del lavoro necessario a risolvere il problema. Il linguaggio ricapitola i progressi concettuali di tutta una storia, e ci fa vedere le cose «dalle spalle dei giganti».
La geometria analitica
La geometria analitica è un’invenzione di Cartesio (René Descartes (1596-1650)) e Pierre de Fermat (1601-1665), intorno al 1630, che ha rivoluzionato la geometria e il suo rapporto con l’algebra. Per gli antichi greci la geometria aveva un ruolo predominante, fondante, rispetto all’algebra. Le operazioni algebriche erano considerate sensate se avevano una interpretazione geometrica: per esempio, il «quadrato» di un numero a era pensato come la misura del quadrato di lato a, piuttosto che la pura e semplice abbreviazione di a x a; per questo motivo, per esempio, a5 non aveva senso per i greci, non potendo immaginare un «ipercubo» in uno spazio di dimensione 5.
La geometria analitica ha capovolto il rapporto tra l’algebra e la geometria. Con l’idea di «sistema di riferimento» e di «coordinate», un punto sulla retta viene identificato con un numero reale, un punto del piano viene identificato con una coppia (x,y) di numeri. Ora ogni figura geometrica piana che sia esprimibile come «luogo geometrico», cioè «insieme di tutti e soli i punti che soddisfano una certa relazione», viene identificato con l’insieme di tutte e sole le coppie (x,y) che soddisfano una certa relazione algebrica (equazione o disequazione), e quindi con l’equazione o disequazione stessa. Rette, circonferenze, parabole diventano così equazioni nelle due variabili x,y. Un semipiano diventa una disequazione nelle due variabili x,y. L’operazione geometrica di intersecare due rette (trovare il loro punto comune) viene tradotto nell’operazione algebrica di cercare la coppia (x,y) che risolve simultaneamente due equazioni, cioè, che risolve il sistema delle due equazioni.
Come si capisce, si tratta di un linguaggio potentissimo. Oggetti e concetti geometrici vengono tradotti in oggetti e concetti algebrici; la potenza di calcolo dell’algebra permette quindi di risolvere analiticamente i problemi; i risultati possono poi essere interpretati geometricamente. Per questa via diventano trattabili problemi che per la geometria tradizionale (o «sintetica») erano inaccessibili o addirittura impossibili da formulare. Per esempio, nello studio delle curve piane, la geometria sintetica tradizionale si era sostanzialmente limitata alla classe delle «coniche» (ellissi, iperboli, parabole) che, dal punto di vista analitico, sono le curve del second’ordine, cioè espresse da un’equazione polinomiale di secondo grado in (x,y). Ora il linguaggio della geometria analitica rende naturale porsi il problema di studiare le curve di grado superiore a 2. Solo poche di queste, però, hanno una definizione «sintetica» naturale, in termini di luoghi geometrici; di tutte le altre la geometria sintetica tradizionale non poteva neppure parlare.
Incontriamo quindi un aspetto nuovo del linguaggio matematico: non solo il linguaggio incorpora in sé idee e progressi di tutta una storia, e quindi «si fa carico» di una parte importante del lavoro necessario a risolvere un problema; il linguaggio amplia anche l’orizzonte concettuale dei problemi che si possono e che è naturale studiare, suggerisce nuove domande, dà nuovi orizzonti alla ricerca.
Sottolineiamo qualcuna delle idee importanti che stanno alla base della geometria analitica e che quindi, storicamente, l’affermarsi di questo linguaggio ha definitivamente incorporato nella matematica corrente.
L’idea che l’insieme dei numeri reali sia una buona rappresentazione dell’insieme dei punti della retta (e viceversa). Col linguaggio attuale, la corrispondenza biunivoca tra punti della retta e numeri reali (corrispondenza percepita oggi così naturale da far sì che i matematici dicano spesso «la retta reale», confondendo perfino linguisticamente l’oggetto geometrico -retta- e l’oggetto analitico -numeri reali-). Questa idea ai tempi di Cartesio poteva solo essere intuita, mancando un’assiomatizzazione rigorosa sia del sistema dei numeri reali (sarà fatta da Richard Dedekind (1931-1916), Georg Cantor (1845-1918), Karl Weierstrass (1815-1897) nel 1872), sia dei fondamenti della geometria (sarà fatta da David Hilbert (1862-1943) nel 1899). Aver posto un’idea così profonda e semplice a fondamento di un’intera disciplina, la geometria analitica, è certamente un punto di non ritorno fondamentale nello sviluppo delle idee matematiche.
L’idea che la geometria euclidea si possa ricostruire dai suoi «teoremi centrali», piuttosto che dai suoi assiomi. Infatti: l’idea di coordinate cartesiane si basa sulle proprietà delle rette parallele; l’equazione della retta si basa sul Teorema di Talete; il calcolo della distanza tra due punti a partire dalle loro coordinate si basa sul Teorema di Pitagora. Con questi concetti, grosso modo, si costruisce tutta la geometria analitica. Il fondamento geometrico della geometria analitica non riposa dunque sugli assiomi della geometria euclidea (che in Euclide, tra l’altro, sono formulati in modo carente, poco utilizzabile per una costruzione rigorosa), ma su pochi teoremi riconosciuti centrali nella geometria euclidea. Possiamo considerare questo punto di vista come uno sguardo pragmatico sulla geometria euclidea, quasi a dire: sulla sistemazione rigorosa dei fondamenti della geometria possiamo litigare all’infinito, ma i fatti centrali della geometria euclidea sono questi: le proprietà delle parallele, il teorema di Pitagora, il teorema di Talete.
Il punto di vista sulla geometria euclidea che consiste nel privilegiare il concetto di luogo geometrico (vedere una figura come insieme di punti con certe proprietà), piuttosto che altre possibili descrizioni delle figure geometriche (per esempio mediante proprietà «globali»). Considerare una figura come un insieme di punti è oggi per noi un fatto naturale, dopo centocinquant’anni dal dilagare in matematica del linguaggio degli insiemi; ai tempi di Cartesio però non era così. Per esempio: per Euclide, un angolo è la parte di piano compresa tra due semirette uscenti da un punto comune; l’espressione «parte di piano compresa fra» non fa riferimento esplicito ai punti del piano; noi ci esprimeremmo piuttosto così: «un angolo è l’insieme dei punti compresi fra due semirette uscenti da un punto comune». È questo punto di vista insiemistico, naturale per noi oggi, quello adatto a essere tradotto nel linguaggio della geometria analitica: i punti si rappresentano come coppie (x,y) di numeri, e una relazione tra i punti diventa una relazione algebrica tra x e y. Il punto di vista analitico-insiemistico che la geometria delle coordinate porta con sé è quindi uno dei presupposti da cui potranno nascere il calcolo infinitesimale del Settecento, il concetto di funzione e l’analisi matematica dell’Ottocento, la teoria degli insiemi del Novecento. Nessuno di questi sviluppi, naturalmente, è un frutto meccanico dei passi precedenti, ma ognuno presuppone i passi precedenti. In questo senso la nascita della geometria analitica getta il seme di una vera rivoluzione.
Marco Bramanti
(Professore di Analisi Matematica presso il Politecnico di Milano)
Note
- Questo scritto costituisce una rielaborazione del testo di una conferenza tenuta il 29/11/2001 all’Università di Cagliari, per le matricole del corso di laurea in matematica.
- I numeri con la virgola furono introdotti in Europa da Simon Stevin nel 1585, quasi 400 anni dopo l’introduzione delle cifre indo-arabe, quindi.
- Mathematical Circles Squared, Prindle, Weber and Schmidt, 1972.
- Questo problema compare nella Parte III del Cap. XII del Liber Abaci. Citato in N. Geronimi: Giochi matematici del medioevo. Bruno Mondadori, 2006, p.6.
- Più una piccola frazione di giorno, che però il problema non chiede di esprimere.
- Un esempio istruttivo di come Al-Kuwaritzmi, matematico arabo del IX secolo a cui si deve il primo trattato sulle equazioni, risolve l’equazione di 2° grado 21 + x2 = 10x è riportato per esempio in Bottazzini, Fregugli, Toti-Rigatelli: Fonti per la storia della matematica. Sansoni, 1999, pp.165-6.
- François Viète, 1591, In artem analyticem isagoge; 1600, Algebra Nova.
Vai alla Seconda Parte dell’articolo pubblicata sul n° 43 di Emmeciquadro
Pubblicato sul n° 42 di Emmeciquadro
