Una breve ma accurata storia della Cosmologia moderna, che inizia nel Novecento. Si parte dalle previsioni teoriche della Relatività Generale e dai dati sperimentali di Hubble sull’espansione dell’Universo, che seppelliscono l’idea, prevalente nei due secoli precedenti, di un Universo statico ed eterno. Si esaminano poi i nuovi modelli di Universo e i motivi dell’affermarsi del Big Bang. Tale modello ha subito, e tuttora subisce, continue modifiche anche grazie ai nuovi risultati sperimentali ottenuti a partire dagli anni Novanta del secolo scorso, che hanno evidenziato una accelerazione nell’espansione dell’Universo e l’esistenza di due enti di natura ancora sconosciuta: la materia e l’energia oscure.
La Cosmologia si propone di dare una «spiegazione» della nascita, dell’evoluzione e del futuro dell’Universo. Essa è vecchia quanto l’uomo, ma per millenni è rimasta una scienza sostanzialmente legata alla filosofia. A partire dagli inizi del XX secolo tuttavia la situazione è cambiata e la Cosmologia è diventata anche una branca delle scienze naturali, grazie alle osservazioni rese possibili dalla strumentazione astronomica divenuta disponibile. Ciò che ha dato il via definitivo è stata la formulazione matematica della Relatività Generale che ha permesso di descrivere in modo accurato e quantitativo il comportamento dell’Universo considerato come una nube di materia distribuita uniformemente, sotto l’azione della forza di gravità (caratterizzata dalla costante di gravitazione universale G).
Il risultato più eclatante fu che, indipendentemente dalla sua estensione finita o infinita, questa distribuzione, e quindi l’Universo, poteva solo contrarsi o espandersi. Questo risultato, già intuito da Isaac Newton (1642-1727) sulla base della sola fisica classica, ma allora accantonato perché attribuito a difficoltà della trattazione matematica, era tanto sconvolgente per la mentalità corrente che immaginava l’Universo immutabile e congelato nella sua bellezza, che perfino Albert Einstein (1879-1955), per quanto aperto alle novità, non esitò a introdurre nelle sue equazioni una forza sconosciuta, descritta per mezzo di una opportuna «costante cosmologica Λ», per controbilanciare gli effetti della forza gravitazionale e bloccare l’espansione e la contrazione dell’Universo. La costante cosmologica è ancora oggi usata per tener conto di eventuali forze sconosciute.
Ma fu ben presto evidente che l’Universo non è statico, con buona pace dei nostri preconcetti. Tra il 1920 ed il 1930 infatti attraverso numerose osservazioni Edwin P. Hubble (1889-1953) fu costretto a concludere che tutte le galassie, se considerate su distanze abbastanza grandi da permettere di ignorare le interazioni tra oggetti vicini, sono soggette a un moto che le porta ad allontanarsi le une dalle altre con velocità V = Ho d, dove V è la velocità relativa tra due galassie e d la loro distanza. La costante Ho, detta di Hubble, abitualmente misurata in km/sMpc e avente le dimensioni dell’inverso di un tempo, rende conto della rapidità con cui l’Universo attuale si espande: la misura accurata del suo valore è quindi fondamentale ed è stata una delle più grandi sfide osservative che gli astronomi hanno dovuto affrontare negli ultimi cento anni. Combinando quindi Relatività Generale e legge di Hubble si era portati a considerare come possibili due classi di modelli.
Una prima classe, dato che l’Universo attuale si espande, prevede che, andando indietro nel tempo l’Universo risulta più compresso, la sua densità aumenta e la distanza tra due generici punti si riduce fino a giungere a un tempo to ˜ d/V = 1/Ho in cui tale distanza è nulla (non occorre pensare che l’Universo si riduca a un punto, se avesse estensione infinita continuerebbe a restare tale; si pensi a una spugna molto estesa che, asciugando, si contrae) e la densità della materia è infinita. Si tratta di una singolarità matematica la cui accettazione sul piano fisico non è semplice, perché a quel punto tutte le leggi fisiche note, inclusa la gravitazione non sono più valide, e crea una cesura con ciò che eventualmente c’era prima di quel momento. Possiamo quindi pensare che l’Universo in cui viviamo oggi abbia avuto inizio uscendo da questa singolarità attraverso una specie di esplosione in un tempo lontano ma finito, che ha iniettato nello spazio-tempo la materia-energia che ha portato all’Universo attuale.
Questa classe di modelli, detta del Big Bang, prevede tre diversi scenari per il futuro:
L’espansione continua indefinitamente con V che diminuisce al crescere di d, ma non si annulla mai completamente (Universo aperto);
L’espansione si arresta (V = 0), ma in un tempo infinito (Universo critico);
L’espansione termina e V diventa nulla dopo un tempo finito, oltre il quale l’attrazione gravitazionale innesca una contrazione della materia fino a portare al Big Crunch, una singolarità simile a (e con le stesse difficoltà di) quella iniziale (Universo chiuso), da cui potrebbe ripartire una nuova espansione dando luogo a un Universo oscillante.
Ciò che permette di distinguere tra questi tre casi è la densità ρ della materia presente nell’Universo e il suo rapporto con la quantità ρc = 3 Ho2/(8πG) detta densità critica. Se ρ < ρc l’energia gravitazionale è inferiore alla densità di energia liberata durante il Big Bang e l’Universo continua a espandersi indefinitamente. Secondo la Relatività Generale che descrive gli effetti gravitazionali come deformazione della geometria dello spazio-tempo, questo caso corrisponde a uno spazio iperbolico. Se ρ = ρc l’espansione si arresta dopo un tempo infinito; la geometria dello spazio-tempo è quella euclidea (geometria piana). Se ρ < ρc l’espansione si arresta dopo un tempo finito e lo spazio è parabolico. In questa classe di modelli la materia-energia che caratterizza l’Universo appare al momento del Big Bang. A seconda del fatto che nell’Universo ci fosse oltre alla materia anche radiazione si poteva distinguere tra Big Bang caldo (con radiazione) o freddo (senza radiazione).
La seconda classe di modelli prevede che l’Universo non abbia né inizio né fine, ma che continui a espandersi rimanendo sempre identico a se stesso. Il modello più famoso di questa classe fu quello dello Stato Stazionario, proposto nel 1948 da Hermann Bondi (1919-2005), Thomas Gold (1920-2004) e Fred Hoyle (1915-2001), che, al fine di mantenere costante la densità dell’Universo, prevedeva iniezione lenta ma continua di materia durante l’evoluzione del sistema Universo (questa «creazione continua di materia» sarebbe comunque tanto piccola da non essere rilevabile sulla scala della vita umana e pertanto non è in contrasto con le osservazioni). Questa classe di modelli ha il vantaggio di non presentare una singolarità iniziale e quindi di preservare la validità delle leggi fisiche che valgono oggi.
La seconda metà del XX secolo
Negli anni Cinquanta e Sessanta del secolo scorso gli astronomi si sforzarono di trovare prove a favore o contro le due classi di modelli dell’Universo risultanti dalla combinazione della Relatività Generale e delle misure di Hubble. La scoperta quasi casuale, nel 1964, della Radiazione Cosmica di Fondo a Microonde o CMB (Cosmic Microwave Background) risolse definitivamente la questione a vantaggio del Big Bang caldo. Fu così possibile cominciare a scrivere la «storia termica» dell’Universo.
Una via d’uscita dalle principali difficoltà dei Modelli a Big Bang, la singolarità iniziale e il problema della «connessione causale», fu trovata introducendo la teoria dell’inflazione che offriva anche suggerimenti sul modo di calcolare lo spettro delle fluttuazioni primordiali, ps(k) = As·kn, necessarie a spiegare la formazione delle condensazioni di materia che caratterizzano l’Universo attuale (k è una misura delle dimensioni angolari delle fluttuazioni).
La CMB, che consente di vedere come era l’Universo quando aveva una vita di soli 300.000 anni circa, ben prima della comparsa degli oggetti osservati dagli astronomi ottici, divenne immediatamente il terreno preferito per le osservazioni di carattere cosmologico. In trenta anni circa, con osservazioni da Terra e dallo spazio, fu possibile concludere che la CMB ha:
Uno spettro di frequenza di tipo planckiano;
Un piccolo grado di anisotropia con spettro angolare caratteristico;
Un piccolo grado di polarizzazione lineare.
Nelle due immagini che seguono sono evidenziate le diversità nella distribuzione della materia e della radiazione. La distribuzione oggi visibile, altamente disuniforme, è caratterizzata da condensazioni di vario tipo (stelle, sistemi stellari, ammassi, galassie, ammassi di galassie) immerse in uno spazio estremamente rarefatto, formatesi dopo che materia e radiazione presenti nell’Universo primordiale hanno smesso di interagire. Questa immagine, ottenuta riportando in diverse direzioni su una fetta di cielo le distanze da noi delle galassie che qui vediamo, (distanze misurate per mezzo della Legge di Hubble) aggiunge la profondità all’immagine piatta del cielo proiettata sulla volta celeste.
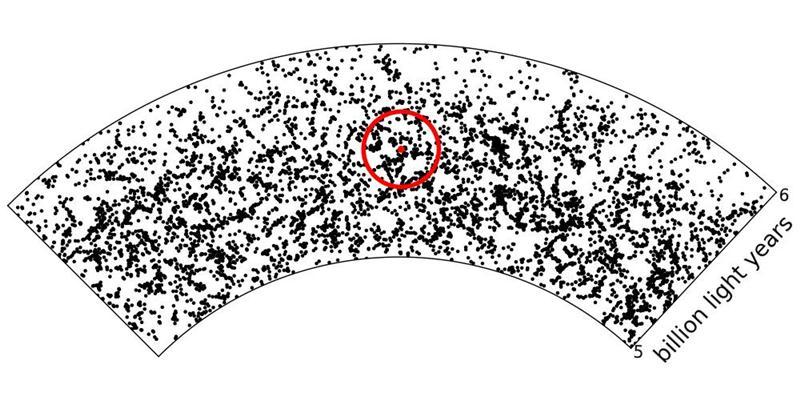
Distribuzione della materia visibile nell’Universo attuale
A differenza di ciò che accade con la materia, la CMB anche oggi riempie uniformemente tutto lo spazio. Per rendere visibili irregolarità nella sua distribuzione spaziale, le cosiddette anisotropie, che appaiono in questa immagine, occorre sottrarre un termine costante circa 100.000 volte più intenso.

Le irregolarità nella distribuzione della CMB
Non sono invece state osservate, nonostante diversi sforzi osservativi, deviazioni dello spettro della CMB da una distribuzione planckiana, dimostrando che l’evoluzione dell’Universo è avvenuta in modo estremamente regolare. Così a poco a poco, a partire dai primi anni Novanta, si è fatto strada il Modello Standard del Big Bang i cui parametri più importanti sono: la costante di Hubble Ho, la densità universale della materia Ωm (in unità di densità critica ρc) e il rapporto primordiale Elio/Idrogeno, la cui storia termica può essere oggi descritta piuttosto dettagliatamente. (cfr. l’Approfondimento: Breve Storia Termica dell’Universo).
Gli ultimi venti anni: il Modello delle Concordanze
Dall’ultimo decennio degli anni Novanta in poi hanno cominciato ad acquistare importanza per la Cosmologia anche osservazioni non basate sulla CMB. Nel giro di pochi anni esse hanno permesso di misurare il red-shift e quindi la distanza di milioni di oggetti extragalattici consentendo la realizzazione di mappe in tre dimensioni della distribuzione della materia condensata (galassie) nell’Universo; hanno fornito grandi campioni di Supernovae ad alto red-shift che sono stati utilizzati per migliorare le stime della densità di materia e dei limiti superiori alla costante cosmologica originariamente ipotizzata da Einstein; hanno mostrato l’esistenza di materia «oscura» (nel senso di «non visibile» ma anche e soprattutto di «natura sconosciuta») in diverse situazioni astrofisiche; hanno rivelato le Oscillazioni Acustiche Barioniche (Barion Acoustic Oscillations) nella distribuzione della materia ordinaria, con spettro angolare di potenza simile allo spettro angolare della distribuzione della CMB; hanno ottenuto la distanza di oggetti a red-shift sempre più alto, quindi sempre più lontani nel tempo e prossimi all’epoca di formazione dei primi oggetti condensati, utilizzando nuovi tipi di «candele standard» (Supernovae di tipo Ia o SNIa e Gamma Ray Bursts). Per non parlare delle simulazioni numeriche (simulazioni a N corpi) con cui si studia la formazione ed evoluzione di condensazioni di materia a partire da una nube uniforme.
L’insieme completo di osservazioni CMB e non-CMB ha portato negli ultimi dieci anni circa a suggerire che la geometria dell’Universo è euclidea (piana) o molto prossima ad essa; che la ricombinazione di nuclei ed elettroni a Z ≈ 1000 è stata seguita da una re-ionizzazione parziale della materia quando si sono formate le prime condensazioni stabili; che dopo aver decelerato l’Universo sta passando attraverso una fase di ri-accelerazione; che per garantire che la geometria dell’Universo sia euclidea è necessario ipotizzare l’esistenza di materia ed energia oscura in quantità molto importanti.
Per rendere conto di questi risultati osservativi sono stati introdotti nuovi parametri cosmologici:
Le abbondanze Ωb, Ωdm e ΩΛ , (Ωx=ρ/ρc), in unità di densità critica, di materia barionica, materia oscura ed energia oscura (occorre ricordare che massa ed energia sono equivalenti per cui la densità di energia può essere espressa come densità di massa);
Lo spessore ottico τ, dell’Universo all’epoca della re-ionizzazione;
As e ns, l’ampiezza e l’indice spettrale delle fluttuazioni;
σ8, un indicatore della uniformità della distribuzione della materia galattica.
Aggiungendo questi nuovi parametri al Modello Standard del Big Bang ne è uscito il Modello delle Concordanze o Λ-CDM, (dove CDM sta per Cold Dark Matter, cioè materia oscura a bassa temperatura). Esso è caratterizzato da sei parametri indipendenti più un certo numero di parametri derivati, combinazioni di quelli indipendenti (si veda l’inserto che segue).
Grandezze fisiche, modelli, parametri, osservabili
I modelli dei sistemi fisici, inclusi i modelli cosmologici, contengono un certo numero di parametri liberi. Tutti i parametri devono essere associati a grandezze fisiche che caratterizzano il sistema («osservabili» nel seguito), misurabili e indipendenti. Il confronto tra i valori misurati delle osservabili e i valori permessi dei parametri permette di testare il modello, cioè «validarlo», migliorarlo o «falsificarlo» secondo un modo di dire alla Popper. Alcune osservabili possono essere misurate direttamente (per esempio il red-shift delle galassie) o attraverso una serie di passi intermedi ben definiti e dipendenti da un modello semplice universalmente accettato (per esempio la distanza di un oggetto con il metodo della parallasse). Chiamiamo «dirette» queste misure. I risultati di ripetute misure dirette indipendenti di un osservabile X formano una serie {X} di numeri da cui con i metodi statistici classici si ricava il valor medio X e la deviazione standard σme che chiamiamo «valori misurati». Il valore X di una osservabile non ancora misurata in modo diretto (per esempio la densità di energia oscura) deve essere ottenuto attraverso «misure indirette» studiando osservabili dette secondarie, legate a X, detta osservabile primaria, attraverso un modello che supponiamo noto. Si raccolgono (attraverso osservazioni o da dati in letteratura) i valori delle osservabili secondarie associate a X, si specifica il modello e si associa a X il valore del parametro MX del modello che meglio si adatta ai valori delle osservabili secondarie. La procedura di adattamento dei dati al modello viene spesso realizzata con il «metodo Monte Carlo»: si calcola ripetutamente MX facendo ogni volta una scelta casuale dei parametri del modello, si fa la distribuzione dei valori ottenuti e si pone X ≈ EM ± σex dove EM , detto «valore atteso», è il valore di MX per cui la distribuzione è massima e σex è la larghezza della distribuzione che racchiude il 68% dei valori di MX. σex non contiene però nessuna informazione sul grado di affidabilità del modello che lega osservabili primarie e secondarie, ed è quindi diverso da σme. Solo se siamo molto confidenti nella bontà del modello possiamo scrivere σme = σex , altrimenti possiamo porre σme = (σex + σpr) dove σpr è una sorta di errore sistematico che rende conto delle incertezze del modello. I modelli cosmologici attuali danno una soddisfacente descrizione della nascita e della evoluzione dell’Universo utilizzando sei parametri indipendenti. Tuttavia la maggior parte delle osservabili associate vengono misurate in modo indiretto. |
Usualmente vengono assunti come indipendenti Ho, Ωb, Ωdm, τ, As e ns, mentre rientrano tra i parametri derivati l’età dell’Universo Tuniv ≈ 1/Ho, la densità critica ρc della materia-energia, la densità (in unità di ρc) di energia oscura ΩΛ, il red-shift Zion al momento della ri-ionizzazione e σ8. Poiché generalmente le osservazioni forniscono combinazioni delle osservabili associate a questi parametri, per separare i parametri si deve ricorrere a complesse operazioni di calcolo. La pratica corrente è adattare (in gergo, fare un fit) il Modello delle Concordanze all’insieme di dati CMB e non-CMB ed estrarre i valori dei parametri che garantiscono il miglior adattamento (best fit) del modello alle osservazioni. Il processo di ottimizzazione viene compiuto con «metodi Monte Carlo» utilizzando «catene di Markov», che consistono nell’utilizzare il modello per calcolare ripetutamente le quantità osservabili partendo da parametri liberi, scelti ogni volta in modo casuale, con l’aggiunta di condizioni a priori che limitano l’intervallo di variabilità dei parametri dei modelli entro limiti ritenuti ragionevoli. Scelte comuni sono Ω = 1 (Universo perfettamente euclideo) e Ω = Ωb + Ωdm + ΩΛ. Analizzando i risultati così ottenuti come fossero risultati di osservazioni si ottengono i valori attesi (expectation values) dei parametri del modello e la loro dispersione (si veda l’inserto precedente). Questi valori vengono poi attribuiti alle osservabili associate, come fossero risultati di misure.
La procedura ormai ben stabilita viene generalmente ripetuta ogni qualvolta nuovi dati significativi vanno ad aggiungersi alla base-dati delle osservazioni. Essa è stata applicata in particolare dopo le osservazioni della CMB compiute dal satellite WMAP e comincia ad essere applicata anche ai recentissimi dati della missione Planck.
Le Tabelle che seguono mostrano esempi dei valori attesi EM così ottenuti e la relativa dispersione σMex per i parametri liberi e derivati del Modello delle Concordanze oggi presenti in letteratura (per maggiori dettagli occorre studiare le singole realizzazioni). Quando disponibili, in Tabella 1 sono riportati anche il valor medio XM e la deviazione standard σMme delle misure dirette X dell’osservabile associata a M.
| parametro/osservabile | valore atteso EM | valore misurato XM | |
| Cost. Hubble (km/s Mpc) | Ho | 70.4 ( +1.3, – 1.4) | 74.2 ± 3.6 |
| Densità Materia Barionica | Ωb | 0.046 ± 0.002 | 0.005 – 1 |
| Densità Materia Oscura | Ωdm | 0.223 ± 0.001 | 0.006 -1 |
| Spess. Ottico ricombinaz. | Τ | 0.09 ± 0.01 | 0.01– 080 |
| Ampiezza flutt.ni scalari | As | (2.44 (0.088, – 0.092)) 10-9 | ? |
| Indice spettrale scalare | ns | 0.963 ± 0.012 | 0.5 – 1.5 |
Tabella 1 – Modello delle Concordanze o Λ-CDM: valori tipici dei valori attesi e dei valori misurati delle osservabili associate ai parametri liberi
| parametro/osservabile | valore atteso | |
| Densità Energia Oscura | ΩΛ | 0.728 (+0.015, -0.016) |
| Red shift riionizzazione | Zion | 10.4 ±1.2 |
| Ampiezza fluttuazioni galattiche | σ8 | 0.809 ± 0.024 |
| Età dell’Universo (anni) | to | (13.75 ±0.11) 10+9 |
Tabella 2 – Modello delle Concordanze o Λ-CDM: valori tipici dei valori attesi (expectation values) di parametri derivati
Conclusioni
Guardando attentamente le due Tabelle balza subito all’occhio che la materia barionica rende conto di meno del 5% della quantità di materia-energia necessaria a rendere la geometria dell’Universo euclidea (Universo piatto). La parte mancante, necessaria a rendere la geometria dell’Universo euclidea, è fornita dalla materia oscura (22% circa) unita all’energia oscura (73%). Inoltre i valori attesi (expectation values) dei parametri del modello hanno barre d’errore (σex) tanto piccole che talvolta si parla, forse un po’ troppo affrettatamente, di Cosmologia di precisione. Sono risultati estremamente interessanti ma occorre fare attenzione. Per cinque dei sei parametri liberi del Modello delle Concordanze le misure dirette delle osservabili associate sono piuttosto povere o non ancora disponibili. In particolare le osservazioni danno solo intervalli piuttosto ampi entro cui cadono, o si aspetta che cadranno, i valori misurati delle densità di materia oscura ed energia oscura. Unica eccezione è la costante di Hubble Ho per la quale ci sono ormai misure dirette molto accurate. Guardando attentamente le due tabelle si nota anche che σMex ≤ σMme o addirittura σMex << σMme. Ciò significa che in alcune situazioni, in cui le ipotesi alla base dei modelli sono deboli, assumere che σMex sia rappresentativa dell’incertezza da associare all’osservabile collegata al parametro M, sia quanto meno ottimistico se non fuorviante. Come detto nell’inserto precedente occorrerebbe aggiungere a σMex qualcosa che sia rappresentativo dell’accuratezza del modello e delle condizioni a priori utilizzati per ricavare σMex.
Possiamo quindi dire che:
Il Modello delle Concordanze fornisce al momento la migliore rappresentazione dell’Universo in cui viviamo;
Tale rappresentazione è la più probabile, ma altri modelli che spieghino la «piattezza» della geometria dell’Universo in cui viviamo, pur essendo meno probabili, non possono essere esclusi definitivamente fino a che non si dimostri che portano a conclusioni in contrasto con le osservazioni;
Occorre pensare ad algoritmi, al momento ancora in via di sviluppo, che consentano di valutare il peso da attribuire a modelli diversi, che non siano stati «falsificati» perché portano a prevedere risultati in contrasto con l’osservazione. Tali algoritmi (di cui non ci occuperemo in questa sede) dovranno essere ottenuti combinando i valori probabili delle osservabili (ottenuti con misure indirette analizzate attraverso i metodi sopra esposti), con i risultati di misure dirette delle stesse osservabili. Si può ragionevolmente assumere che un modello sia tanto più probabile quanto minore è la differenza tra σMex e σMme;
Alla luce del punto precedente sembra evidente che per l’immediato la cosa più urgente sia migliorare l’accuratezza delle misure dirette delle osservabili associate ai parametri liberi del Modello delle Concordanze.
Sicuramente in futuro il Modello delle Concordanze verrà superato da modelli più accurati, ma questo non vorrà assolutamente dire (a meno che si trovino errori nelle analisi che hanno portato alla sua formulazione) che il modello è sbagliato: ogni modello è una migliore approssimazione del modello che lo ha proceduto e una prima approssimazione del modello che lo seguirà. Per esempio la scoperta della CMB ha «falsificato» il modello dello Stato Stazionario e «validato» quello del Big Bang caldo. Questo ultimo è poi evoluto nel Modello Standard del Big Bang e quindi in quello delle Concordanze.
Un fatto di cui i cosmologi sono divenuti consapevoli è che l’Universo che descriviamo con il Modello delle Concordanze potrebbe essere un Universo particolare all’interno di un Universo fatto a bolle e ciascuno di questi Universi può nascere da un proprio Big Bang ed evolvere in un modo diverso, a seconda di cosa c’era all’inizio del suo Big Bang. Se questi diversi Universi comunicano in qualche modo tra di loro si può ritenere che in un futuro potremo pensare a osservazioni che ci parlino di loro. Se invece questi Universi non comunicano, al momento sembra difficile poter immaginare di riuscire a studiarli. Ma occorre essere molto cauti nel dire «mai!». Ricordiamo che qualche secolo fa, prima della scoperta della spettroscopia, un famoso filosofo scienziato aveva affermato che mai l’uomo avrebbe potuto conoscere la composizione delle stelle.
Vai all’intero articolo in formato PDF
Giorgio Sironi
(Professore Ordinario di Radioastronomia presso l’Università degli Studi Milano-Bicocca)
© Pubblicato sul n. 50 di Emmeciquadro
