Una conversazione con l’ingegner Sergio Serapioni consente di accostare il pluriennale lavoro di ricerca che lo ha portato a elaborare una teoria unificata e geometrica della fisica a partire da uno spazio a cinque dimensioni.Con semplici relazioni geometriche Serapioni è in grado di render conto di diversi aspetti fisici e anche dei valori numerici delle costanti universali.Pur non avendo ancora una formalizzazione assiomatica, la teoria di Serapioni è in grado di ottenere alcune quantità, come l’età dell’Universo e il suo contenuto di materia oscura, che risultano in buon accordo con le osservazioni cosmologiche.
L’ingegner Sergio Serapioni si dedica (e il verbo non è scelto a caso in quanto trattasi di una vera e propria passionale dedizione) da più di quarant’anni ad un – vogliamo chiamarlo hobby?, interesse? No, io lo chiamo lavoro il cui scopo è quello di fornire una visione unitaria del mondo fisico. La costruzione di Serapioni è un modello autoconsistente che cerca in maniera assolutamente originale di rispondere ad alcuni dei quesiti ancora aperti ed insoluti della fisica moderna e della cosmologia.
In questo saggio proveremo a introdurre e spiegare i punti salienti della costruzione di Serapioni: avremo modo di conoscere concetti come rotazione, velocità e tempo che risultano fondamentali per la comprensione piena del modello proposto.
Partiamo quindi dalle premesse, dalle idee di base su cui tutta la costruzione si poggia saldamente: è la ricerca di una teoria unificata e geometrica di tutta la fisica. In questo Serapioni si trova in ottima compagnia: già il grande Albert Einstein aveva espresso il desiderio di spiegare la fisica in termini geometrici.
Occorre fare una precisazione fondamentale. La geometria tratta di enti geometrici (il punto, la retta, le stesse figure geometriche) che per loro stessa natura (matematica) sono “perfetti”, cioè non esistono nella realtà fisica. Ad esempio un corpo rigido non esiste esattamente in natura in quanto le proprietà di rigidità di un corpo solido dipendono dalla sua temperatura, dalla sua composizione chimica e dalla sua struttura atomica interna. Di questo fatto Serapioni è perfettamente consapevole e mai si stanca di dire, come fa tutt’ora a più di novant`anni, che in natura non esiste un cerchio di cui si conosca veramente la lunghezza delle circonferenza: la realtà si fermerà necessariamente a una qualche cifra del valore di π, ponendo così fine alla corrispondenza perfetta tra realtà ed enti matematici-geometrici.
Ma questo non impedisce che possa esserci e vada comunque ricercata un’analogia geometrica della fisica. Quindi, immediatamente, ecco il primo problema che Serapioni si trova ad affrontare, quello dello spazio, del palcoscenico su cui gli enti geometrici (che rappresentano le grandezze fisiche, quindi nella loro accezione reale) e le relazioni tra essi (che codificano invece le leggi fisiche) si trovano ad operare.
La nostra mente è abituata, anzi è fatta proprio in modo da visualizzare e cogliere la geometria in uno spazio a tre dimensioni. Perché quindi aggiungerne altre? I motivi sono molteplici.
Einstein per poter accomodare i fenomeni dell’elettromagnetismo ed in particolare la costanza della velocità della luce (essa è sempre la stessa indipendentemente dal moto dell’osservatore in contraddizione con le leggi di composizione delle velocità della fisica galileiana basata su spazio e tempo assoluti) ha introdotto uno spazio a quattro dimensioni in cui il tempo ha perso quel valore assoluto (esso scorre in maniera identica per ogni osservatore e non dipende dal moto dell’osservatore stesso) ed assume invece le caratteristiche di un’ulteriore coordinata allo stesso livello delle tre coordinate spaziali.
Per descrivere un evento, un certo fenomeno fisico, non basta sapere dove questo avvenga ma anche quando questo abbia luogo. Così facendo fu necessario modificare in maniera sostanziale le trasformazioni di Galileo che permettevano di legare i risultati ottenuti da un osservatore con quelli ottenuti da un altro osservatore in moto rispetto al primo.
Con il tempo che non è più assoluto le trasformazioni di Galileo non forniscono un’adeguata descrizione della realtà. Esse sono sostituite dalle trasformazioni di Lorentz in cui entra in maniera esplicita la costanza e finitezza della velocità della luce (per quanto un valore – 300.000 km/s – che nella nostra esperienza quotidiana è assimilabile ad un valore infinito).
Se fosse infinita (o meglio per tutti quei fenomeni in cui possiamo pensare che essa sia infinita) le trasformazioni di Lorentz si riducono a quelle di Galileo.
Su questa linea di pensiero ci potremmo quindi chiedere se le trasformazioni di Lorentz siano le più generali possibili. In effetti il matematico italiano Luigi Fantappiè fu in grado di generalizzare le trasformazioni di Lorentz ad un gruppo di trasformazioni ancora più generale che le comprende e a cui si riduce nel caso di un universo con un raggio infinito.
Queste trasformazioni descrivono uno spazio a cinque dimensioni. Se possiamo in qualche modo accettarne quattro immaginando il tempo come una “foliazione” dell’usuale spazio a tre dimensioni, cinque sono proprio difficili da immaginare!
Quindi è lecito chiedersi se ci sia una qualche evidenza di uno spazio a cinque dimensioni o se questo è puramente un artificio matematico. Serapioni nella sua trattazione originale e partendo da semplici considerazioni termodinamiche di equipartizione dell’energia arriva a supportare l’idea di uno spazio penta-dimensionale. Ma anche la cosmologia viene in nostro aiuto. Infatti dalle recenti misure della radiazione cosmica di fondo (l’eco più remota dell’universo primordiale) fornite dal satellite PLANCK dell’Esa si può stimare l’età dell’Universo che risulta di circa 14 miliardi di anni. Conseguentemente il raggio dell’universo, per quanto incredibilmente grande, è comunque finito.
Quindi a livello cosmologico sarebbe adeguato fare uso delle trasformazioni di Fantappiè e quindi di uno spazio a cinque dimensioni per la descrizione dei fenomeni fisici.
A partire da questo spazio a cinque dimensioni Serapioni costruisce tutta la sua teoria fisica in cui con semplici relazioni geometriche è in grado di render conto di diversi aspetti della fisica (forze, velocità, accelerazioni eccetera) ed anche dei valori numerici delle costanti universali.
In particolare quest’ultimo punto è un aspetto che sempre ha tormentato Serapioni: perché le masse delle particelle hanno certi valori? Come questi sono definiti?
Anche Richard Feynman era estremamente insoddisfatto proprio di questo punto. Serapioni è però convinto della possibilità di costruire una teoria che accomodi in maniera naturale i valori numerici di masse e di costanti. Non si tratta di numerologia di bassa lega ma di una costruzione coerente di un universo da cui emergono i concetti di spazio, tempo, massa ed energia.
Una teoria fisica coerente in se stessa deve essere, da un lato, in grado di spiegare la realtà per come essa si racconta ai nostri occhi ma, molto più importante, deve essere in grado di fare predizioni su quantità osservabili (e non ancora osservate) in modo che la teoria possa essere rifiutata oppure accettata fino a quando non sarà eventualmente in grado di rendere ragione di un dato sperimentale.
L’altro punto fondamentale su cui proveremo a soffermarci ulteriormente che sta alla base del lavoro di Serapioni è il fatto che l’unica interazione (sia auto-interazione che interazione tra enti) è il movimento (come già sosteneva Heisenberg) e che l’unico movimento possibile sono rotazioni. Per questo il modello di spazio a cinque dimensioni di Fantappiè ben si presta allo scopo. Ma non basta. Infatti il modello di Fantappiè descrive un mondo perfetto, incarna una idealità di un universo perfettamente geometrico nel senso matematico del termine e che quindi non ha alcuna attinenza con la realtà fattuale ed esperienziale.
È infatti un universo banale perché vuoto. Lo spazio di Serapioni è invece uno spazio popolato da particelle sia ordinarie (elettroni, protoni, neutroni eccetera) sia esotiche (materia oscura) e che comprende inoltre ogni forma di energia compresa anche quella misteriosa energia oscura che sembra guidare, secondo le osservazioni cosmologiche di supernove lontane, l’evoluzione dell’Universo attuale.
Lo spazio a cinque dimensioni
Abbiamo detto che gli unici movimenti possibili nello spazio proposto da Serapioni sono rotazioni ed è attraverso queste rotazioni e alle velocità con cui esse avvengono che sono descritte le particelle e le leggi della fisica.
Mi preme sottolineare a questo punto l’intuizione originale di Serapioni di pensare alle rotazioni come pilastro fondamentale della sua teoria. Da un punto di vista astrofisico, ogni oggetto che noi osserviamo è in movimento e questo movimento è sempre riconducibile ad una rotazione.
La Terra ruota intorno al Sole che a sua volta ruota intorno al buco nero al centro della nostra galassia che a sua volta ruota intorno al centro di massa del gruppo locale di galassie.
Si potrebbe obiettare che questo moto di rotazione delle stelle sia vero per le galassie a spirale (dove le orbite delle stelle sono ordinate) ma non per quelle ellittiche o irregolari dove le orbite non sono ordinate ma caotiche, ma comunque anche per queste galassie le stelle ruotano intorno al loro centro.
Anche a livello microscopico ed atomico le rotazioni sono sempre presenti. La domanda a questo punto è spontanea: da dove viene questa rotazione? Come nasce? Perché gli oggetti sono in rotazione?
Potremmo pensare, come in effetti per molte delle situazioni citate è il caso, che l’origine della rotazione sia legata ad un raggiungimento di una configurazione stabile all’interno di un campo, quello gravitazionale, che agisce. Ma questo non spiega il perché un oggetto quasi isolato come una nube molecolare gigante, in grado di formare stelle, debba essere in rotazione: senza questa rotazione non si avrebbe formazione di un disco di materia intorno alla nascente stella da cui si originerebbero poi i pianeti. La rotazione è quindi fondamentale!

È questo quindi un problema interessante e il lavoro di Serapioni getta una luce nuova anche su questo aspetto. Nel farlo chiama in causa un altro grande del passato come Poincaré (anche in questo l’approccio di Serapioni è interessante: coglie il nocciolo nel lavoro di grandi del passato e lo sfrutta, lo rielabora all’interno del suo modello) di cui sfrutta l’ormai non più famosa congettura.
Essa afferma, in termini matematici, che una varietà n-dimensionale semplicemente connessa immersa in uno spazio n + 1-dimensionale è l’unica varietà senza buchi. Tradotto in termini più comprensibile: una sfera (più propriamente una 2-sfera) immersa in uno spazio tridimensionale è una varietà semplicemente connessa.
La congettura di Poincaré può in questo contesto fornire una descrizione appropriata delle rotazioni nello spazio a cinque dimensioni. Questo spazio non è uno spazio usuale in cui le dimensioni sono tutte allo stesso livello. Esso è composto da uno spazio a tre dimensioni di cui siamo soliti fare esperienza e da uno spazio a due dimensioni con dimensioni estremamente piccole (a livello sub-atomico) e di cui non ci rendiamo conto nella nostra esperienza sensoriale.
Sono quindi due spazi che insieme compongono lo spazio della teoria ma che mantengono la loro propria caratteristica e peculiare identità. Le rotazioni avvengono quindi, seguendo Poincaré, contemporaneamente sia su una 3-sfera che su una 2-sfera.
Queste due rotazioni nello spazio complessivo della teoria su di una varietà 4-dimensionale che si può dimostrare essere semplicemente connessa e che quindi risulta simile (il termine corretto è omeomorfa) ad una 4-sfera.
Non sono concetti facili da immaginare (non siamo infatti in grado di immaginarci una 4-sfera). Potremmo immaginare una sfera con i paralleli ed i meridiani che costituiscono una griglia di coordinate sulla sua superficie e che ad ogni intersezione di meridiani e paralleli sia posta un’altra sfera. In questo la matematica fornisce uno strumento descrittivo anche laddove la nostra immaginazione visiva non riesca ad arrivare.
Ecco quindi che abbiamo a disposizione il palcoscenico penta-dimensionale della teoria e gli enti (dai moti dei quali Serapioni deriva le costanti e le leggi della fisica) ruotano in questo spazio.
Rotazioni a cinque-dimensioni
Nei diversi discorsi che ho avuto modo di fare con Serapioni, è sempre emerso un punto interessante per me. Se è vero che gli unici movimenti sono rotazioni e che queste avvengono contemporaneamente nello spazio a tre ed a due dimensioni, mi chiedo che relazione esista tra queste due rotazioni. Ma soprattutto esiste una tale relazione (non abbiamo infatti a priori nessuna garanzia che questa debba esserci)?
Per rispondere a questa domanda occorre introdurre un parametro fondamentale della teoria (che appare anche nelle espressioni che definiscono le masse delle particelle) che viene indicato con la lettera θ e che oggi assume un valore estremamente piccolo (dell’ordine di 10−21).
Tale parametro evolve nel tempo ed è legato all’emergenza dello spazio tridimensionale. Infatti nel modello si è posto l’universo al Big Bang fosse puramente bidimensionale e che θ fosse uguale a π/2 cioè 90◦. Nel tempo questo parametro decresce, da un lato, facendo emergere lo spazio a tre dimensioni e, dall’altro, rendendo sempre più piccole le dimensioni dello spazio bidimensionale originario.
Tornando quindi alle rotazioni abbiamo che inizialmente un ente può ruotare unicamente in uno spazio bidimensionale. L’evoluzione successiva di θ permette che esso possa iniziare a ruotare contemporaneamente nello spazio tridimensionale che viene ad emergere. Quindi le rotazioni nei due spazi non sono allo stesso livello e il legame tra esse è proprio dato da θ.
Edwin Hubble nel 1926, misurando distanze e velocità di circa una quarantina di galassie vicino alla nostra, scoprì che l’universo è in espansione: più osserviamo oggetti lontani più questi appaino allontanarsi da noi con una velocità che è direttamente proporzionale alla loro distanza.
In cosmologia si è soliti descrivere matematicamente l’espansione dell’universo tramite una funzione a(t) detta fattore di scala.
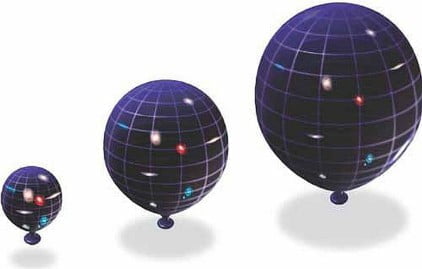
Per visualizzare questo fatto immaginiamo di disegnare una serie di punti sulla superficie di un palloncino e di cominciare a gonfiarlo. La latitudine e la longitudine di una qualunque coppia di punti è fissata, ma l’effetto dell’espansione è quello di ingrandire il raggio del palloncino e quindi di aumentare la distanza tra i due punti. Il fattore di scala in cosmologia descrive esattamente questo effetto.
Si potrebbe quindi pensare che il parametro θ evolva come il fattore di scala. Infatti tanto più θ decresce tanto più emerge lo spazio tridimensionale e tanto più a(t) cresce. Purtroppo questa non può funzionare in quanto non è in grado di rendere ragione delle osservazioni cosmologiche tramite la radiazione cosmica di fondo.
Nel modello del Big Bang Caldo l’universo, nelle sue primissime fasi è caratterizzato da condizioni estreme di densità e temperatura per poi raffreddarsi per effetto dell’espansione: In pochi minuti raggiunge le temperature presenti nei nuclei delle stelle realizzando le stesse reazioni di fusione nucleare che portano alla formazione di elio e pochi altri elementi leggeri.
Nella teoria di Serapioni i valori di masse e cariche delle particelle (neutroni, protoni ed elettroni) dipendono dal valore estremamente piccolo di θ. E da questi valori dipendono i meccanismi fisici delle reazioni nucleari che sappiamo essere avvenuti nell’universo primordiale.
Pertanto anche se inizialmente θ = π/2, quasi immediatamente con l’inizio dell’espansione esso deve assumere il valore attuale in modo da garantire il corretto “funzionamento” dei meccanismi fisici necessari all’evoluzione dell’universo così come esso ci appare. È quindi necessario quasi una transizione di fase che immediatamente porta θ ad assumere il suo valore odierno.
Velocità delle rotazioni e costanti fondamentali
Per poter cogliere al meglio il concetto di rotazione di un ente nel modello di Serapioni e quali conseguenze esso abbia, occorre introdurre il concetto di evento. Esso è definito come il tempo che un ente impiega a percorrere una particolare orbita.
In uno spazio penta-dimensionale avremo complessivamente un insieme di rotazioni, ognuna in un piano ortogonale alle altre e con raggi ∆Ti con i = 1, . . . , 4 definiti dalla relazione
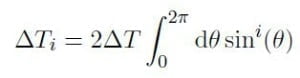
in modo che il loro prodotto sia esattamente uguale al volume dell’ipersfera i-dimensionale di raggio ∆T. Il raggio fondamentale per Serapioni è il raggio classico dell’elettrone definito come πλ0 per cui
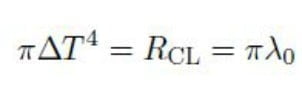
Quindi un evento (che normalmente ha una connotazione temporale) è associato ad una rotazione e questo sarà anche per il concetto di tempo (notiamo che in questo modo una lunghezza assume le dimensioni di un tempo alla quarta potenza, la velocità sarà un tempo alla terza, mentre un’accelerazione un tempo alla seconda).
Il tempo scorre dal passato al futuro passando nel tempo “nullo” del presente senza privilegiare alcuna precisa direzione nelle rotazioni che lo rappresentano. Pertanto nello spazio penta-dimensionale, dove i movimenti come sappiamo sono unicamente rotazioni, avremo un moto di rotazione in cui l’accelerazione cambia istante per istante (se non altro come direzione e verso come in un moto circolare).
Serapioni deriva da questa situazione il concetto di istante: esso è il tempo necessario per modificare l’accelerazione della rotazione.
Sfruttando quindi la struttura dello spazio a cinque dimensioni e del gruppo di Fantappiè, Serapioni arriva dunque a definire complessivamente 5 accelerazioni ortogonali tra di loro. Il fatto che siano proprio ortogonali è legato alla struttura dello spazio come composizione (prodotto tensoriale) di uno spazio tri- con uno bi-dimensionale.
Questo è sicuramente l’aspetto più originale nella costruzione di Serapioni. Esisterà dunque un rapporto ben preciso e definito tra i tempi di rotazione nei due spazi. Nel gruppo di Fantappiè sappiamo che c, la velocità delle luce, è la velocità con cui ruotano gli enti.
Supponiamo che un ente in rotazione con una velocità ωxyz nello spazio tridimensionale lungo una circonferenza di raggio R1. Possiamo scrivere quindi R1 = ct1 associando quindi al raggio della circonferenza il tempo t1 impiegato a percorrerla, mentre ωxyz = dθ/dt è associata all’angolo θ descritto durante l’intervallo di tempo t1.
In questo modo si ottiene un’equazione differenziale che fornisce il rapporto tra il tempo t1 ed il tempo fondamentale (la costante di integrazione dell’equazione) t0. A questa rotazione occorre inoltre associare la rotazione che avviene nello spazio sottostante bidimensionale. Immaginando quindi che la distanza R1 sia a sua volta una circonferenza di raggio R2 che viene percorsa con velocità angolare ωST otteniamo il rapporto
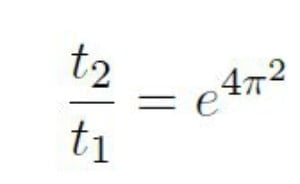
Da questo rapporto è possibile ricavare (si veda l’articolo “Il sorriso dell’ingegnere” pubblicato sul n° 49 – Giugno 2013 di Emmeciquadro)) l’età dell’universo che risulta essere in un accordo estremamente preciso con le misure ottenute dalle osservazioni del fondo cosmico fornite dai satelliti WMAP della Nasa e PLANCK dell’Esa.
In quanto appena esposto ritroviamo il modulo fondamentale πλ0. Serapioni a partire da questo modulo (e da altre – poche per la verità – quantità) riesce a ricostruire tutti i valori numerici delle costanti della fisica come, ad esempio, la velocità della luce, la costante di gravitazione universale di Newton.
Le quantità necessarie ad ottenere questo risultato sono sia quantità puramente numeriche (come π, 2 e 3 che rappresentano le dimensione degli spazi della teoria, l’angolo θ) sia quantità più fisiche come γ che è legata alla variazione di entropia che è richiesta per la creazione delle strutture ordinate della teoria stessa.
Vettori polari
Il metodo usato da Serapioni per la descrizione delle rotazioni nello spazio penta-dimensionale (3+2) fa ricorso ai vettori polari. Questi permettono di descrivere rotazioni in maniera semplice ed immediata.
Sappiamo che normalmente le rotazioni possono essere o destrorse o sinistrorse e che la combinazione di una rotazione destrorsa con una sinistrorsa con la stessa ampiezza, cioè con lo stesso angolo, produce una rotazione nulla.
In ogni caso i rotori risultanti dalle composizioni delle rotazioni sono sempre ortogonali al comune spazio a tre dimensioni. Questi vettori descrivono appunto le rotazioni degli enti della teoria. Complessivamente abbiamo un totale di 9 vettori polari per ogni singolo piano di movimento, ottenuti dal prodotto vettore dei vettori velocità e distanza istantanei
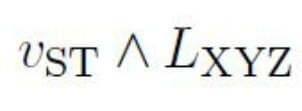
ed essendo dieci i piani distinti in uno spazio penta-dimensionale, avremo un totale di 90 rotazioni ammissibili che ovviamente comprendono sia rotazioni “reali” (che cioè avvengono nello spazio tridimensionale usuale) sia rotazioni apparenti o astratte.
Considerando unicamente rotazioni nello spazio sottostante, quindi invisibile alla nostra esperienza, otteniamo un sott’insieme delle rotazioni con cui potremo formare 5 grandezze istantanee che risultano avere dimensioni di una massa. Ma pur avendo le stesse dimensioni ed avendo anche lo stesso effetto fisico (generano un campo gravitazionale) la natura di queste 5 masse è diversa dalle masse della nostra esperienza sensoriale.
Queste masse astratte possono avere un “influsso” sulle masse reali solo a patto di renderle fattuali. Esso sono infatti masse che potremmo definire disordinate, cioè masse senza una struttura come potrebbe essere quella di un solido cristallino. Occorre renderle ordinate e per fare questo sarà inevitabilmente necessario fornire una quantità di energia o esse dovranno dedicare parte della loro energia a questo scopo.
Pertanto nel computo totale dell’energia associata a queste masse non basterà moltiplicarne il valore per la velocità c della luce al quadrato come ci insegna Einstein (E = mc2) ma occorrerà quantificare l’energia spesa nella loro creazione.
Abbiamo prima accennato al coefficiente entropico γ che rappresenta, dicendolo in un modo immediato, la quantità di energia che è necessario spendere per creare una struttura ordinata. È una quantità molto prossima all’unità ma nel computo dell’energia associata a tutte le possibili rotazioni avremo un fattore γ per ognuna delle rotazioni possibili. Pertanto avremo un fattore γ90 per il computo totale dell’energia mentre questo esponente sarà 70 per le cinque masse
istantanee o astratte. Quindi abbiamo una fattore γ70 per le masse astratte che rappresentano masse a noi invisibili (come la materia oscura presente nell’universo) mentre avremo un fattore γ90 per tutta l’energia associata alle rotazioni degli enti. Per le masse ordinarie (quelle di cui facciamo normalmente esperienza) non abbiamo alcun fattore di riduzione entropico in quanto tali masse, per loro natura, sono già ordinate.
Possiamo quindi provare a calcolare i valori delle densità associate alle varie masse. Il computo dell’energia totale legata alle rotazioni degli enti sarà:
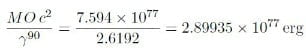
Per ricavare l’energia totale dovremo aggiungere quella associata alla materia ordinaria, che come detto è già ordinata avremo
M c2 = 1.518 × 1077 erg
Per la materia oscura avremo il rapporto MO c2/γ70.
Il rapporto tra quest’ultima quantità e la densità totale dell’universo fornisce un valore che ancora una volta è in ottimo accordo con le misure cosmologiche sia dalle survey di galassie (come la Sloan Digital Sky Survey o la 2 degree field) che con le misure del fondo cosmico.

Conclusioni
Abbiamo voluto presentare in questo breve lavoro alcuni degli spunti originali ed interessanti del lavoro pluridecennale dell’ingegner Sergio Serapioni.
Non si tratta di un percorso fisico ortodosso, da libro di testo. Ma ciò nonostante esso è in grado di fornire una spiegazione ad alcune delle questioni ancora aperte delle fisica e della cosmologia: perché le masse delle particelle hanno proprio certi valori? Da dove vengono? È possibile ricavarli da una teoria generale?
Serapioni con un approccio geometrico prova a dare una risposta in tal senso. Nella sua costruzione tutto è legato ad un semplice movimento quello di una rotazione. Per ora la teoria, pur non avendo ancora una formalizzazione assiomatica da teoria fisica standard, è in grado di ottenere alcune quantità come ad esempio l’età dell’Universo ed il suo contenuto in termini di materia oscura, che risultano in buon accordo con le osservazioni cosmologiche.
In un prossimo futuro sono previste diverse missioni spaziali che miglioreranno la nostra conoscenza dell’universo in cui viviamo e sarà interessante verificare la consistenza delle previsioni della teoria di Serapioni.
Ancora una volta: ai posteri l’ardua sentenza.
Davide Maino(Ricercatore confermato presso il dipartimento di Fisica dell’Università degli Studi di Milano – Sezione Fisica dei Plasmi e Astrofisica. E’ fra i principali responsabili scientifici del Data Processing Center di LFI, la parte italiana della strumentazione di bordo situata sul satellite europeo Planck)