Un’appassionata ricerca teorica ha portato Sergio Serapioni a sviluppare l’approccio relativistico di Fantappiè per costruire un nuovo modello di Universo: una cosmologia «geometrizzata», dove le cinque dimensioni spaziali hanno la natura di un tempo.
Un lavoro ancora in progress, che ha trovato una sorprendente conferma calcolando l’età dell’Universo con un valore del tutto compatibile con quello recentemente ricavato dai dati della missione PLANCK.
Finalmente ci siamo! Dopo un lavoro durato più di vent’anni (dalla progettazione alla realizzazione e infine alle operazioni nello spazio) finalmente il satellite PLANCK dall’Agenzia Spaziale Europea ha fornito i suoi primi risultati di interesse cosmologico.
Dopo il lancio avvenuto con successo dalla base di Kourou (Guyana Francese) il 14 maggio 2009 e dopo un’impeccabile funzionamento, sono stati presentati alla 47a Conferenza ESLAB nella sede di ESTEC dell’ESA vicino a Noordwijk, le primizie cosmologiche di PLANCK basate sulle osservazione relativi ai primi 15 mesi di missione. PLANCK ha infatti scandagliato le profondità dell’Universo misurando, con precisione mai raggiunta prima, l’eco primordiale del Big Bang, il primo segnale che l’Universo ha dato di se stesso: la radiazione cosmica di fondo o CMB (Cosmic Microwave Background).
Questa è una radiazione che permea l’intero Universo, estremamente debole (in termini di temperatura la sua intensità è di soli 2.7 gradi sopra lo zero assoluto) e che presenta piccole fluttuazioni dell’ordine di una parte su 100.000, quindi di poche decine di micro-Kelvin. Grazie al fatto che la velocità della luce ha un valore, incredibilmente alto, ma finito l’osservazione della CMB è una grande macchina del tempo che ci permette di risalire a un’epoca in cui l’Universo aveva solo 380.000 anni: PLANCK ha permesso di ricavare con maggiore precisione il momento esatto, o meglio l’intervallo di tempo, in cui la CMB si è originata e di stimare anche l’età dell’Universo che è risultata di 13,81 miliardi di anni con un’accuratezza circa tre volte superiore rispetto alla precedente stima. È quindi grande la soddisfazione degli oltre quattrocento scienziati di tutto il mondo che hanno lavorato alla realizzazione di questo potente strumento di indagine cosmologica.
Ma la soddisfazione è anche per i non addetti ai lavori. Gioisce infatti del risultato sull’età dell’Universo ottenuto da PLANCK, un distinto ingegnere di quasi 89 anni, Sergio Serapioni, che nel 1998 aveva ricavato questo risultato in base alla teoria di spazio e tempo da lui sviluppata nell’arco di diversi anni. 
Imprenditore lombardo di successo a livello nazionale, intorno ai 50 anni Serapioni riscopre l’amore per la fisica e comincia ad approfondirne sia gli aspetti termodinamici, di cui si era occupato per la propria attività imprenditoriale, sia quelli cinematici.
[A sinistra: Luigi Fantappié (1901-1956)]
Durante questa ricerca si imbatte nei lavori di Luigi Fantappié, matematico romano amico di Fermi, i cui lavori sono ormai dimenticati forse per l’atmosfera carica di un finalismo religioso nelle sue ultime riflessioni sul cosmo.
Non si può tuttavia dimenticare quel che di interessante, da un punto di vista puramente scientifico, Fantappié aveva trovato: le usuali trasformazioni utilizzate in fisica, quelle di Galileo (che esprimono l’invarianza della meccanica newtoniana) e quelle di Lorentz della relatività speciale (che esprimono l’invarianza anche dell’elettromagnetismo), non sono altro che un caso particolare di una più generale classe di trasformazioni, quelle appunto di Fantappié, che risultano invece essere le più generali trasformazioni possibili.
Esse rappresentano le trasformazioni di uno spazio a quattro dimensioni con curvatura costante che si può immaginare come una superficie penta-dimensionale, analogamente a come una superficie bi-dimensionale a curvatura costante (una sfera) viene normalmente immaginata come iper-superficie in uno spazio a tre dimensioni. In questo spazio a cinque dimensioni gli unici movimenti permessi sono rotazioni (destrorse o sinistrorse) e gli unici parametri fondamentali sono la velocità della luce c, e il raggio Ru del cronotopo.
Da questa struttura Serapioni parte nella costruzione del suo modello di Universo.
Spazi multi-dimensionali
L’uso di spazi ad alta dimensionalità è pratica abbastanza comune in molte teorie fisiche: la relatività di Einstein lavora in uno varietà 4-dimensionale mentre le moderne teorie delle stringhe postulano l’esistenza di 11 dimensioni. La costruzione geometrica fatta da Serapioni, come suggerito dal gruppo di Fantappié, prevede uno spazio a 5 dimensioni.
L’idea fondamentale della teoria è quella di un modulo base da cui poter ricavare sia le grandezze fisiche che i valori numerici delle costanti della fisica. Novello Archimede, Serapioni è andato alla caccia di questo modulo fondamentale λ0.
Quello dell’origine delle grandezze fisiche è un aspetto delicato in quanto, nell’usuale spazio fisico ordinario è necessario introdurre i concetti di massa, carica, forza che non sono implicitamente definiti. Nella teoria in esame abbiamo tre dimensioni che sono le usuali dimensioni spaziali di cui facciamo esperienza quotidianamente, mentre le restanti due dimensioni sono estremamente piccole, o meglio i moti – cioè le rotazioni come supposto da Fantappié – avvengono con velocità angolari estremamente piccole e pertanto trascurabili. 
L’idea di Serapioni costituisce un tentativo di geometrizzare la fisica. Infatti in questo modello il volume di ipercubi 4-dimensionali è associato al nostro usuale concetto di lunghezza che pertanto è una quantità non più fondamentale, ma derivata a partire dal modulo fondamentale λ0. Per poter costruire altre grandezze fisiche occorre specificare da un lato le dimensioni fisiche di λ0 e dall’altro aggiungere il concetto di movimento: tale movimento sarà, come già implicito nel gruppo di Fantappié, una rotazione.
Quali dimensioni ha quindi λ0? La novità introdotta da Serapioni è che ognuna delle 5 dimensioni dello spazio abbia la natura di tempo, in maniera simile a quanto accade nella teoria delle stringhe dove anche le particelle nascono da oggetti monodimensionali (le stringhe) che oscillano.
In questo contesto una lunghezza avrà quindi le dimensioni di un tempo elevato alla quarta potenza, mentre la velocità (variazione dello spazio percorso nell’unità di tempo) sarà un tempo alla terza e analogamente, l’accelerazione sarà un tempo alla seconda. È questa una semplice geometrizzazione della fisica: le velocità infatti non sono altro che il volume di un cubo tridimensionale, mentre l’accelerazione è una superficie bidimensionale nello spazio a 5 dimensioni.
Come possiamo descrivere il movimento in un tale spazio? Ricordiamo come già detto che gli unici movimenti possibili sono rotazioni. Pertanto supporremo il moto come un insieme di rotazioni ognuna in un piano ortogonale ai rimanenti con raggi ΔT1, ΔT2, ΔT3 e ΔT4 definiti dalla formula:
in modo che il loro prodotto sia sempre pari al volume dell’ipersfera i-dimensionale di raggio ΔT. Ma un volume 4-dimensionale è una lunghezza e possiamo quindi definire la quantità fondamentale ΔT uguagliando il volume dell’ipersfera S4 al raggio classico dell’elettrone re.
In questo modo otteniamo che ΔT4 = λ0 = re/π.
A partire dai raggi di rotazione definiti precedentemente possiamo derivare il modulo di una distanza fondamentale, pari alla somma in quadratura dei suddetti raggi, che ha le dimensioni di un tempo. Questa quantità tornerà utile nelle derivazione dell’età dell’Universo.
Enti in rotazione e il nuovo π
Ma effettivamente cosa ruota nello spazio in rotazione postulato da Serapioni? Questo è sicuramente il punto più oscuro della derivazione della teoria: egli suppone degli enti che vivono nello spazio a 5 dimensioni e che siano in movimento quindi in rotazione.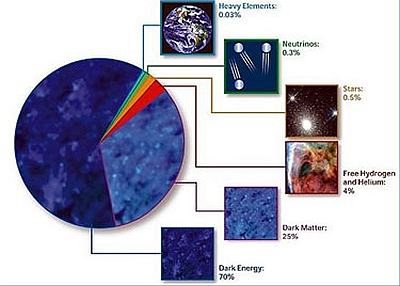 
[A sinistra: il grafico a torta mostra le percentuali dei vari componenti dell’Universo]
Manca ancora una evidenza sperimentale circa l’esistenza di questi enti, che ricordano molto il concetto di etere; ma resta il fatto che dall’interazione reciproca di questi enti e dalle rotazioni che essi compiono si possono ricavare in maniera naturale i concetti di massa e carica delle particelle. Non è qui la sede per parlare di questo: per i nostri scopi relativi all’età dell’Universo conta solo la natura delle rotazioni.
Come ricordato, uno degli elementi fondamentali del gruppo di Fantappié è la velocità della luce c che è supposta essere la velocità con cui ruotano gli enti (in realtà nella derivazione di quanto segue non è necessario che tale velocità sia effettivamente c).
Consideriamo un ente in rotazione con velocità angolare ω1 lungo una circonferenza di raggio L1. Possiamo scrivere: L1= ct1 e in questo modo associamo a L1 il tempo necessario a percorre tale distanza mentre ω1= dθ=dt1 è la velocità angolare cioè la variazione dell’angolo θ spazzato durante il tempo t1.
Sostituendo nell’espressione L1ω1= c otteniamo un’equazione differenziale risolvibile separando le variabili e che fornisce il risultato:
t1/t0 = e2π
Che esprime il legame tra un tempo fondamentale t0 e il tempo t1 impiegato dall’ente a percorre l’orbita. Possiamo ulteriormente supporre che la massima distanza L1 sia in realtà una circonferenza di raggio r2 percorsa con una velocità angolare ω2. In modo analogo alla precedente derivazione, possiamo ricavare il legame tra il tempo fondamentale t0 e il nuovo tempo t2 che conterrà un ulteriore termine esponenziale per cui:
Il termine 
è il nuovo π con cui possiamo ricavare l’età dell’Universo. In linea di principio trattandosi di uno spazio multi-dimensionale si dovrebbe poter continuare e considerare le ulteriori due rotazioni ma come già ricordato le velocità angolari lungo le due dimensioni extra sono estremamente piccole e pertanto possiamo trascurare tali rotazioni.
L’età dell’Universo
A questo punto siamo in grado di ricavare l’età dell’Universo all’interno della teoria di Serapioni. Consideriamo t2 = tU pari cioè all’età attuale dell’Universo mentre possiamo assumere t0=1s. Tale assunzione può sembrare arbitraria ma è possibile dimostrare come questo valore sia in realtà legato solo a costanti fondamentali (quali la costante di struttura fine) e a un altro parametro della teoria che regola l’emergenza dello spazio 3D come lo conosciamo a partire dallo spazio generico 5D.
A questo punto prima di procedere è opportuno notare che un ente in rotazione nello spazio a 5 dimensioni si muove sempre con velocità unitaria in quanto l’intervallo di tempo tra due eventi è assunto pari alla lunghezza dell’orbita percorsa dell’ente che li unisce. Pertanto tempo e spazio nello spazio a 5 dimensioni sono concetti intercambiabili. Ricordando la definizione dei raggi di rotazione ΔTi possiamo definire degli intervalli di tempo secondo
e quindi il modulo temporale dato dalla somma in quadratura dei singoli ti con i = 1,….,4. Pertanto ricaviamo tU che convertito in anni risulta tU = 13.7375 . 109 anni.
È questo già un ottimo risultato, in quanto il valore dell’età dell’Universo fornito dal satellite WMAP della NASA, dopo nove anni di osservazioni combinati con altre informazioni cosmologiche, era risultata pari a 13.772 . 109 anni mostrando come la teoria sia perfettamente in linea con le osservazioni.
Tuttavia occorre tenere presente un punto fondamentale, ma per ora non toccato, legato alla natura del modello di Serapioni la cui natura geometrica è costituita da strutture ordinate. Sappiamo dalla fisica, e più precisamente dalla termodinamica, che la quantità fisica che descrive lo stato di ordine – o di disordine – di un sistema è l’entropia ed essa è una quantità che tende a crescere in quanto ogni sistema tende inesorabilmente al disordine. Un classico esempio è fornito dalle molecole di una gas in un recipiente inizialmente confinate in un angolo dello stesso: esse tenderanno a distribuirsi in maniera uniforme all’interno del recipiente. Per descrivere lo stato iniziale è necessario fornire una quantità di informazioni elevata mentre per il secondo stato è sufficiente definire la temperatura del sistema e il tipo di gas che lo costituisce.
Pertanto lo creazione di strutture ordinate comporta una diminuzione di entropia che, nel modello di Serapioni, è possibile dimostrare essere corrispondente a una contrazione di volumi e quindi anche delle lunghezze. Il modello di Universo di Serapioni, come già ricordato, prevede uno spazio a 5 dimensioni di cui 3 sono le ordinarie dimensioni di cui facciamo esperienza, mentre le altre 2 extra dimensioni sono oggi estremamente piccole. Ma non è sempre stato così.
Noi oggi sappiamo che l’Universo, secondo il modello dell’Hot Big Bang, parte da una singolarità spaziale per poi espandersi come mostrato da Hubble nel 1926 e confermato sempre più precisamente oggi. Ma questo ancora non basta e siamo costretti per poter spiegare quello che le osservazioni cosmologiche ci mostrano, a postulare una fase di espansione esponenziale avvenuta nelle primissime frazioni di secondo di vita dell’Universo che prende il nome di inflazione. In maniera analoga il modello di Universo di Serapioni era inizialmente caratterizzato da solo 2 dimensione e le 3 dimensioni dello spazio usuale erano piccolissime come richiesto dalla singolarità iniziale. Nelle prime fasi per un meccanismo altrettanto misterioso come quello dell’inflazione, le due dimensioni extra dell’Universo si sono contratte fortemente «lasciando il posto» all’usuale spazio tridimensionale.
Pertanto, quando abbiamo stimato l’età dell’Universo non abbiamo tenuto conto che stiamo considerando una struttura geometrica che è contratta di una quantità pari alla diminuzione di entropia al quadrato, in quanto abbiamo uno spazio a sole due dimensioni. Numericamente questo fattore è rappresentato da un altro parametro fondamentale della teoria ε = 1.00268. Pertanto moltiplicando per ε2 la stima dell’età dell’Universo otteniamo 13.811 miliardi di anni in perfetto accordo sia con WMAP che con il miglior recente risultato di PLANCK.
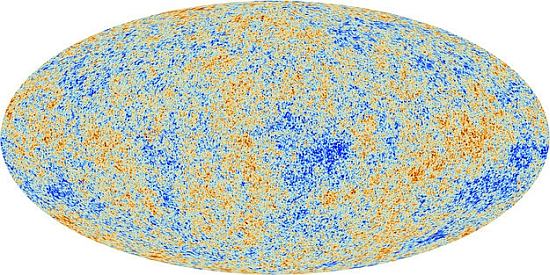La mappa della Radiazione Cosmica di Fondo (CMB) ottenuta dai dati del Satellite Planck
Ai posteri l’ardua sentenza
I risultati ottenuti all’interno della teoria proposta da Serapioni sono diversi e vanno oltre quello qui riportato circa l’età dell’Universo, tanto da essere in grado di riprodurre in maniera notevole i valori numerici delle costanti fisiche. Semplice coincidenza? Solo una questione di numerologia?
La domanda è lecita e a mio avviso necessita di una risposta. Certo non è semplice districarsi all’interno delle matematica e della logica espressa da Serapioni in circa 40 anni di lavoro su questa teoria. Ma con pazienza è possibile trovare intuizioni geometriche interessanti e innovative che possono gettare una luce nuova sul nostro modo di vedere e approcciare i problemi più interessanti e ancora aperti della fisica moderna quali il legame tra la descrizione classica dell’Universo fornita dalla relatività generale di Einstein e quella dell’infinitamente piccolo della meccanica quantistica.
Questo di Serapioni è un tentativo di unificazione delle due teorie più di successo dell’ultimo secolo e come tale merita un esame e studio più approfondito.
Davide Maino
(Ricercatore confermato presso il dipartimento di FISICA – Sezione Fisica dei Plasmi e Astrofisica. E’ fra i principali responsabili scientifici del Data Processing Center di LFI, la parte italiana della strumentazione di bordo situata sul satellite europeo Planck)
© Pubblicato sul n° 49 di Emmeciquadro
