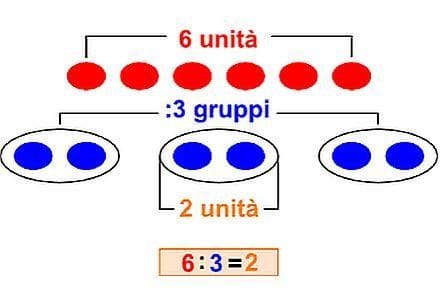
L’autore chiarisce la struttura presente in alcuni problemi di moltiplicazione e divisione. Si limita ai numeri naturali molto piccoli perché intende unicamente esemplificare la struttura.
Questo articolo vuole chiarire la struttura soggiacente ad alcuni problemi di moltiplicazione e di divisione.
L’autore limita il campo della riflessione ai numeri naturali molto piccoli perché in questa sede intende unicamente esemplificare la struttura: il lettore potrà passare a numeri interi grandi e a numeri razionali.
Scopo del lavoro da proporre agli allievi è mostrare la natura delle corrispondenze e lo schema con cui si possono rappresentare, sul quale ci si può orientare con facilità in molti casi di problemi con moltiplicazioni e divisioni.
L’argomento può essere iniziato nella scuola primaria e ripreso nella scuola secondaria di primo grado, ma non è da escludere a priori dal biennio della scuola superiore.
Le indicazioni didattiche, del tutto generali, possono essere precisate a seconda del livello scolastico e del percorso eventualmente già attuato.
Il concetto di corrispondenza è molto generale. La parola deriva dal latino medievale «correspondere», composto di cum (con, insieme) e respondere (rispondere) che significa «essere conforme».
In matematica due insiemi (che possiamo chiamare e ) di elementi (non necessariamente della stessa natura) sono posti in corrispondenza se a elementi dell’uno vengono associati (cioè corrispondono) elementi dell’altro. Attraverso una corrispondenza si formano coppie ordinate di elementi (a, b) dove a appartiene ad e b appartiene a (a ![]() , b
, b ![]() ).
).
Una corrispondenza in cui a ogni elemento di corrisponde un solo elemento di , si dice funzione f di su . In questo caso la corrispondenza si dice univoca da verso ; se la si rappresenta con un diagramma a frecce, da ogni elemento di parte una freccia e questa freccia è unica. Su alcuni elementi di possono arrivare molte frecce: vuol dire che parecchi elementi di hanno lo stesso corrispondente in .
Una corrispondenza si dice biunivoca se a ogni elemento di corrisponde un solo elemento di e viceversa (quindi è univoca sia da verso che da B verso ). Se la si interpreta con il linguaggio delle funzioni, essa determina sia una funzione f di su che una funzione g di su e le due funzioni f e g si dicono una l’inversa dell’altra. Se si usa come rappresentazione un diagramma a frecce, da ogni elemento di parte una, e una sola freccia, e ogni elemento di è raggiunto da una, e una sola freccia.
I casi che esamineremo di seguito riguardano invece corrispondenze in cui a ogni elemento di un insieme corrispondono più elementi dell’altro. Esse si dicono «plurivoche» o «non univoche» (questo fatto può capitare andando da verso B, oppure da verso A, oppure in entrambi i versi).
Vai al PDF dell’intero articolo
Anna Paola Longo
(Docente di Analisi matematica. Politecnico di Torino)
© Pubblicato sul n° 36 di Emmeciquadro