Il concetto di funzione fa parte dei contenuti che più caratterizzano il linguaggio matematico come un modo di «parlare» della realtà. Guardando la storia del pensiero scientifico, lo si riconosce come un frutto maturo del processo di algebrizzazione e di simbolizzazione, perché in esso confluiscono le possibilità espressive dei simboli, unite alla forza rappresentativa della geometria, particolarmente con la rappresentazione cartesiana. Infatti, è stato lo sviluppo dell’analisi infinitesimale a partire dal XVII secolo a introdurre l’idea e la possibilità di trattare una funzione come un vero e proprio «oggetto» matematico, di complessità certamente superiore a numeri e figure, che più facilmente identifichiamo come campo di azione della matematica. Se nell’immaginario collettivo un matematico è un personaggio un po’ perso nel suo mondo numerico, chi sa qualcosa di matematica potrebbe più probabilmente affermare che un matematico vive e pensa negli spazi funzionali, espressione che però non sarebbe facilmente compresa.
Nel percorso di formazione matematica mi pare perciò importante che tale concetto venga riconosciuto e assunto come uno dei nodi concettuali più significativi, da «far crescere» pazientemente, ma consapevolmente, nell’arco del cammino scolastico, fino a una piena messa a fuoco nella scuola superiore. Significati, lessico, e rappresentazioni, relativi alle funzioni, vanno trattati assai prima di parlare di analisi matematica, in modo da preparare il terreno per i metodi infinitesimali così ricchi ed eleganti, ma anche così complessi, attraverso i quali si porta a nuovi livelli l’astrazione algebrica e geometrica.
Tenere presente fin dai primi anni il concetto di funzione è una buona occasione per presentare la matematica come un sapere che si occupa di «relazioni» e che fa uso di procedimenti e metodi profondamente razionali, non rigidamente determinati.
Tanto più che oggi disponiamo di strumenti tecnologici che non solo permettono di superare le difficoltà dei calcoli numerici e algebrici più complessi, ma addirittura offrono rappresentazioni grafiche certamente superiori a qualunque linea tracciata a mano, magari anche la visione tridimensionale di funzioni in più variabili.
Ci si può chiedere perciò se ha ancora un senso, e una qualche utilità, proporre agli studenti il complesso esercizio dello «studio di funzione», che si conclude in un grafico completo della funzione, in cui si evidenziano visivamente le sue caratteristiche fondamentali, e si raccolgono tutte le informazioni provenienti dal calcolo. Si tratta di uno dei problemi più ricchi e belli della matematica liceale che generalmente, superati i primi scogli concettuali, gli studenti apprezzano, soprattutto se lo si presenta come una ricerca ragionevole e coerente di informazioni, non come tecnica raffinata, ma standardizzata.
Tuttavia, oggi la questione è rovesciata, perché possiamo «partire» dal grafico: prima di aver calcolato limiti e derivate, vediamo già sullo schermo di qualunque calcolatrice grafica o del portatile (usando software scaricabili gratuitamente dalla rete) dove e quali sono i massimi e i minimi, la tendenza alla frontiera e quanto altro interessa.
Credo che sia una bella sfida da raccogliere: per fare una semplice analogia, è chiaro che guidare una Ferrari richiede più «capacità» ed «esperienza» che guidare una Cinquecento, non di meno! Occorrerà insegnare la matematica non per le sue tecniche, ma per il suo significato, per la portata della sua forma concettuale, bisognerà dedicare tempo e interesse alla risoluzione e all’impostazione dei problemi, bisognerà riportare, una volta di più, la nostra attenzione ai «perché» e non soltanto al «come».
L’articolo che presentiamo è uno stimolo interessante in questa direzione.
Raffaella Manara
(Docente di Matematica alle Scuole Superiori. Fa parte della Redazione di Emmeciquadro)
A cosa serve studiare il grafico di una funzione? E ancora prima, cosa è il grafico di una funzione? Non voglio qui dare una definizione aulica, come quelle che si trovano sui testi di Analisi Matematica, ma riflettere su diversi possibili modi di affrontare a scuola la conoscenza di una funzione, sottolineando collegamenti e significati.
Cosa si può conoscere di una funzione senza farne il grafico? Una volta data la definizione, corredata da dominio e codominio, si possono ricercare analiticamente asintoti, intervalli di monotonia, massimi, minimi, concavità, flessi, punti di discontinuità della funzione e delle sue derivate. Per comodità di lettura si può riportare tutto su una tabella. Con alcune convenzioni grafiche, tutto questo si può riportare anche su un grafico nel piano cartesiano.
Cosa aggiunge il grafico? Certamente visualizza in modo sintetico le informazioni note, rendendo più evidenti i loro legami, suggerisce inoltre di fare controlli sui calcoli quando emerge qualche incongruenza. Il grafico fornisce un’utile visione sintetica, ma non offre certezze se è staccato dalle dimostrazioni analitiche. Esso si limita a restituire le informazioni che vi sono state immesse; può inoltre suggerire ipotesi di altre proprietà che, se interessano, vanno dimostrate.
Sulla tabella riassuntiva delle proprietà o sul grafico, gli elementi costitutivi della funzione sono pronti per l’uso, a seconda dei significati attribuiti alle variabili e al contesto in cui la funzione serve come strumento. Anche dentro la matematica si può incontrare un uso strumentale delle funzioni, per esempio quando si integra. Entriamo in questo campo per esaminare qualche esempio.
Se ci si chiede se sia possibile definire un integrale di funzione razionale in un intervallo [a,b], occorre essere certi che in tale intervallo la funzione sia continua. Trattandosi di una funzione razionale, questo accade sostanzialmente se in [a,b] la funzione non ha asintoti verticali. La conoscenza delle caratteristiche di f(x), riassunte nella tabella complessiva o trasferite nel grafico, basta certamente per rispondere, ma rileviamo che lo studio completo contiene proprietà sovrabbondanti. Per il nostro fine, infatti, basta conoscere solo il dominio e gli asintoti verticali: potrebbe bastare una tabella ridotta, oppure un grafico «qualitativo» che riporti solo gli elementi selezionati come interessanti.
Ecco un esempio.
Se la funzione da integrare è f(x) = (x3+3x-1)/ (x2-1), si cercano gli zeri del denominatore (x = 1 e x = -1), si verifica che non annullino il numeratore (1+3-1 ≠ 0 ; -1-3-1 ≠ 0), e si conclude che f(x) non è integrabile in intervalli che contengano x = 1 oppure x = -1 (o entrambi). Sarà integrabile per esempio in [-1/2, 1/3] oppure in [10, 15] ma non in [-3/2, 2]. Si noti che se in uno dei due punti si annullasse anche il numeratore, si avrebbe una discontinuità eliminabile, che non toglie l’integrabilità.
Integriamo ora la funzione![]() (radice del modulo di cosx); di quali elementi della funzione ci può essere utile la conoscenza?
(radice del modulo di cosx); di quali elementi della funzione ci può essere utile la conoscenza?
f(x) è sempre definita, è positiva, è periodica con T = 2π, è continua e certamente limitata. Se vogliamo avere una visione sintetica, possiamo ricercare un grafico «minimo» senza farne uno studio completo. Ci sono vie semplici per ottenerlo senza fare molti calcoli, vie di cui, successivamente, vogliamo esaminare alcuni esempi, valorizzando al massimo la via grafica.
Abbiamo detto che il grafico visualizza le informazioni note e le sintetizza, permette una visione delle sue proprietà più globale della tabella riassuntiva, ma possiamo interrogarlo solo sulle proprietà che abbiamo immesso in esso. Dunque un grafico è da intendersi come una «memoria» sintetica delle proprietà accertate di una funzione. Per utilizzarlo come «memoria», dobbiamo essere certi di quale sia il suo reale carico di informazioni. Se questo è assicurato, saper leggere un grafico si presenta come una questione interessante, anzi direi fondamentale, per poter comprendere, in una grande varietà di campi, le informazioni inserite in un testo (di fisica, storia o altro) mediante il linguaggio delle funzioni.
Per fare questo occorre avere padronanza delle definizioni di base, per esempio massimi, minimi, monotonia, concavità, asintoticità. L’uso di limiti e derivate, che fornisce informazioni utilissime per disegnare i grafici di funzioni, lavora sotto particolari condizioni, contenute nelle ipotesi dei teoremi su cui si appoggiano i «metodi» utilizzati.
L’abitudine a prescindere dalle dimostrazioni, un’eccessiva meccanicità nell’uso di formule, un’acritica fiducia nei calcoli conducono talvolta a ignorare le condizioni sotto le quali si lavora, provocando errori anche su funzioni molto elementari. Per questo ritengo che non sia opportuno introdurre «metodi», senza prima aver fatto un adeguato lavoro sulle definizioni, che porta a fissare immagini e relazioni. Parimenti, per ogni condizione (necessaria o sufficiente) che si introduce attraverso le derivate, è utile presentare dei controesempi abbastanza intuitivi da imprimere nella mente.
Oltre all’integrale definito esistono in matematica altre applicazioni (integrali impropri, equazioni differenziali, serie) in cui occorre solo l’andamento qualitativo dei grafici in un intervallo, che si può individuare senza appesantirne lo studio con numerosi calcoli.
Monotonia di una funzione discontinua
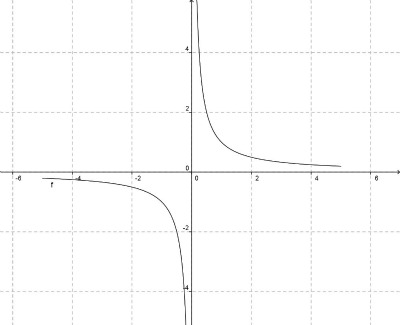 La funzione y = 1/x, discontinua in x = 0, non è né crescente né decrescente nel suo dominio (x ≠ 0), mentre è decrescente se considerata separatamente per x < 0 oppure per x > 0. Uno sguardo superficiale al grafico (riportato a fianco) potrebbe convincere che essa sia decrescente in tutto il suo dominio, ma non è così, come possiamo constatare per tappe successive.
La funzione y = 1/x, discontinua in x = 0, non è né crescente né decrescente nel suo dominio (x ≠ 0), mentre è decrescente se considerata separatamente per x < 0 oppure per x > 0. Uno sguardo superficiale al grafico (riportato a fianco) potrebbe convincere che essa sia decrescente in tutto il suo dominio, ma non è così, come possiamo constatare per tappe successive.
Consideriamola solo su x > 0, e verifichiamo che in questo dominio è decrescente.
Secondo la definizione, considerate due ascisse generiche x1 e x2 del suo dominio (in questo caso positive), posto x1 < x2 , diciamo che f(x) è crescente se e solo se: x1 < x2 → f(x1) ≥ f(x2) per ogni coppia di ascisse scelte.
Cioè l’immagine f(x1) supera l’immagine f(x2) ogni volta che x1 è minore di x2 [Chiamiamo f(x) strettamente crescente se è sempre f(x1) ≠ f(x2)]
Verifichiamolo per x > 0 con un semplice calcolo.
Nel nostro caso f(x1) = 1/x1 e f(x2) = 1/x2; cerchiamo le soluzioni della disequazione f(x1) > f(x2) : 1/x1 > 1/x2 → 1/x1 – 1/x2 >0, → (x2 – x1)/x1x2 >0, da questa (ricordando che il denominatore è positivo) si ricava: x2 – x1 > 0 che è vero ogni volta che è x1 < x2, come abbiamo supposto per ipotesi.
Possiamo specificare che siccome f(x1) ≠ f(x2) per ogni coppia di ascisse positive, f(x) è strettamente decrescente.
Con analoghi calcoli si dimostra che y = 1/x, considerata solo su x < 0, è (strettamente) decrescente. Per dimostrare che la funzione y = 1/x , considerata in tutto il suo dominio (x ≠ 0), non è né crescente né decrescente, basta un contro-esempio. Se fosse decrescente dovrebbe sussistere la relazione precedente per qualsiasi scelta di x1 e x2 , con x1 < x2 anche discordi. Per x1 < 0 e x2 > 0 è f(x1) < 0 e f(x2) > 0. Quindi è chiaramente f(x1) < f(x2), che contraddice la definizione. È sufficiente scegliere x1 = -4, x2 = 3, f(-4) = -1/4, f(3) = 1/3, e si trova una eccezione al comportamento atteso.
Questa dimostrazione diretta, senza l’uso di derivate, obbliga ad applicare la definizione ed è perciò una buona via per comprenderla e memorizzarla.
Se decidessimo di cercare le informazioni nella derivata, ricordiamo che per la funzione y = 1/x la derivata è y’ = -1/x2 . Qualcuno direbbe che è «sempre» negativa e che quindi f(x) è «sempre» decrescente.
Attenzione, dal segno della derivata si può dedurre la monotonia di una funzione solo in un intervallo in cui f(x) sia continua, e tutto si accorda con i calcoli fatti perché f(x) è continua per x < 0 oppure per x > 0, ma non in qualsiasi intervallo che contiene x = 0. L’uso della parola «sempre» è inadeguato.
Monotonia di y = x2
È una funzione ben nota, definita per ogni x reale, pari, sempre positiva, una parabola che ha l’asse y come asse di simmetria. Non lasciamoci suggerire proprietà dal grafico.
Cerchiamo di appurare se è crescente o decrescente utilizzando solo la definizione. Chiamiamo x1 e x2 due ascisse, con x1 < x2 , e confrontiamo le rispettive ordinate affidandoci alla definizione e al calcolo. Abbiamo:
f(x1) = x12 e f(x2 ) = x22; f(x1) < f(x2) diventa:
x12 < x22; x12 – x22 < 0; (x1 – x2) ( x1+ x2) < 0.
Conosciamo il segno del primo fattore del prodotto: da x1 < x2 segue x1 – x2 < 0; quindi il prodotto ha il segno di x1 + x2.
Se ci mettiamo in condizioni di sicurezza, abbiamo che certamente per x > 0 è x1 + x2 > 0, quindi f(x1) < f(x2), e f(x) è crescente; per x < 0 è x1+x2 < 0 , quindi f(x1) > f(x2), e f(x) è decrescente.
Se invece prendiamo x1 < 0 e x2 > 0, non abbiamo nessuna sicurezza del segno della loro somma, cade quindi la possibilità che f(x) sia crescente (o decrescente) su tutto il campo reale.
Guardando un grafico della parabola y = x2 fatto dal computer troviamo la visualizzazione del risultato.
Massimi e minimi in punti di non derivabilità
Esempio 1
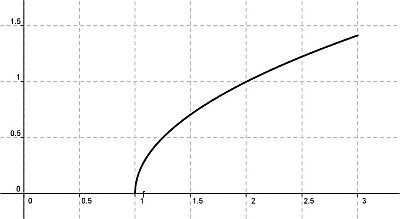 Occupiamoci della funzione
Occupiamoci della funzione![]() nell’intervallo chiuso [1, 3], il cui grafico è mostrato a fianco.
nell’intervallo chiuso [1, 3], il cui grafico è mostrato a fianco.
La derivata è la funzione![]() , che non è definita in x = 1, non ha zeri in (1,3] ed è ivi positiva.
, che non è definita in x = 1, non ha zeri in (1,3] ed è ivi positiva.
Si può dedurre che f(x) è crescente e che non ha minimi e massimi in [1, 3]?
La condizione, (necessaria) per l’esistenza di un massimo o minimo relativo, che sia Df(x) = 0, vale solo per i punti di derivabilità interni al dominio, quindi possiamo solo concludere che f(x) non ha massimi e minimi relativi nell’intervallo aperto (1, 3). La ricerca nei punti x = 1 e x = 3, estremi del dominio, va fatta ricorrendo alle definizioni.
In x = 1 è f(1) = 0 e f(x) > 0 per x(1, 3]; quindi questo punto è minimo relativo (esiste un intorno in cui lo è) e assoluto (lo è in tutto il dominio di f(x)). Si noti l’intervallo aperto a sinistra. In x = 3 si ha invece un massimo (relativo e assoluto) perché il fatto che f(x) sia crescente assicura che f(x) < f(3) per x [1, 3). Si noti l’intervallo aperto a destra.
Esempio 2
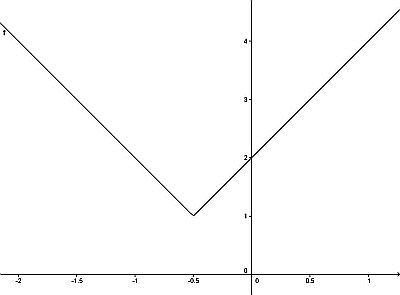 Occupiamoci ora di y = 1+|2x+1|, definita per ogni x reale. Si può trasformare in una «funzione a tratti»:
Occupiamoci ora di y = 1+|2x+1|, definita per ogni x reale. Si può trasformare in una «funzione a tratti»:
y = 1+2x+1 = 2(x+1) per x ≥ -1/2;
y = 1-2x-1 = -2x per x ≤ -1/2,
di cui è immediato fare il grafico, riportato a sinistra.
Per f(x) il punto di ascissa x = -1/2 è un punto di continuità, in cui non esiste la derivata.
Esso è tuttavia un punto di minimo (relativo e assoluto) in quanto è f(x) ≥ f(-1/2) per ogni x reale (verificare con i calcoli ciò che il grafico suggerisce).
Monotonia di funzione composta
Uno strumento importante per abbreviare i calcoli è la possibilità di prevedere la monotonia per una funzione composta di due funzioni monotòne.
Se si compongono due funzioni della stessa monotonia (entrambe crescenti o entrambe decrescenti) la funzione composta è crescente, se si compongono due funzioni di monotonia diversa (crescente, decrescente oppure decrescente, crescente) la funzione composta è decrescente.
Studiamo alcuni casi particolari, lasciando al lettore la dimostrazione del caso generale.
Esempio 1
In 0 < x < π consideriamo f(x) = 1/sinx, funzione composta di f1(x) = sinx e f2(x)= 1/x (gli estremi x = 0 e x = π vanno tolti dal dominio perché la funzione seno, posta al denominatore, si annulla). 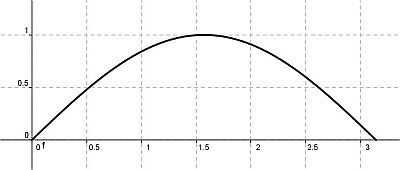 Seguiamo le tappe della composizione:
Seguiamo le tappe della composizione:
x → sinx = t → y = 1/t = 1/sinx.
Otteniamo facilmente un’informazione per l’immagine della funzione composta: 0 < sinx ≤ 1 (vale 1 in π/2, interno all’intervallo considerato). Il grafico di y = sinx è mostrato nel grafico a destra. 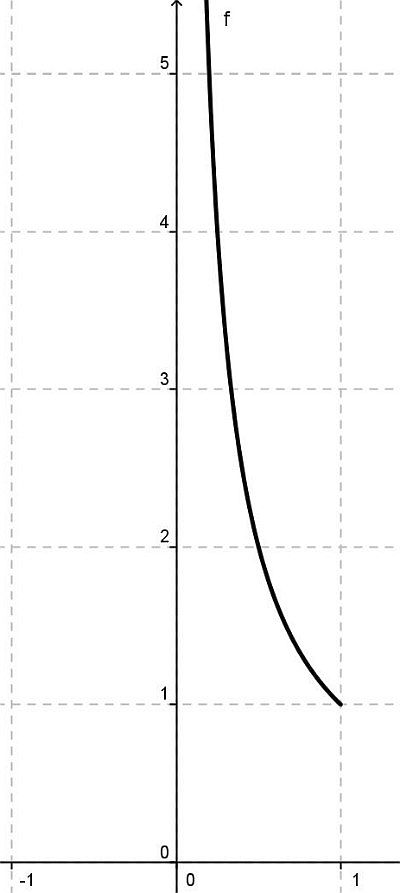 Segue che 1/sinx ≥ 1: le immagini sono positive e maggiori o uguali a 1. Consideriamo perciò la funzione y = 1/t solo per x
Segue che 1/sinx ≥ 1: le immagini sono positive e maggiori o uguali a 1. Consideriamo perciò la funzione y = 1/t solo per x ![]() (0, 1], ottenendo il grafico riportato a sinistra.
(0, 1], ottenendo il grafico riportato a sinistra.
La funzione seno cambia monotonia nell’intervallo scelto, separiamo allora i due casi, quando è crescente oppure quando è decrescente:
Caso 1
0 < x ≤ π/2 : x1 < x2 → sinx1 < sinx2 → 1/t1 > 1/t2 → 1/sinx1 > 1/sinx2
Interpretiamo quanto ottenuto confrontando la prima diseguaglianza con l’ultima: x1 < x2 → 1/sinx1 >1/sinx2
L’ordine delle ascisse non viene conservato tra le immagini, ma si trasforma nell’opposto, quindi la funzione composta è decrescente (nei passaggi intermedi il verso è cambiato una sola volta).
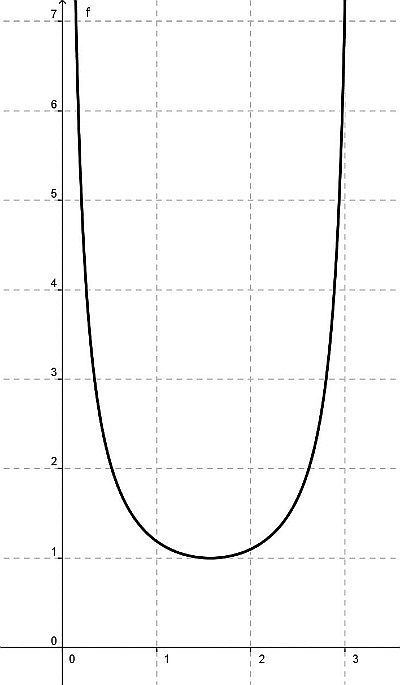 Caso 2
Caso 2
π/2 ≤ x < π : x1 < x2 → sinx1 > sinx2 → 1/t1 >1/t2 → 1/sinx1 < 1/sinx2
Interpretiamo confrontando inizio e fine: x1 < x2 → 1/sinx1 < 1/sinx2; nei passaggi intermedi l’ordine è cambiato due volte, complessivamente l’ordine delle ascisse viene conservato tra le immagini, quindi la funzione composta è crescente.
A destra è mostrato il grafico di 1/sinx nell’intervallo (0,π).
Si può fare il grafico senza bisogno di calcolare limiti: quando x si avvicina a x = 0, anche sinx si avvicina a 0 e 1/sinx si può rendere maggiore di ogni numero positivo.
Esempio 2
Studio del grafico di ![]() per x
per x ![]() [-π/2, 3π/2] attraverso deduzioni successive.
[-π/2, 3π/2] attraverso deduzioni successive.
A) grafico di y = cosx: 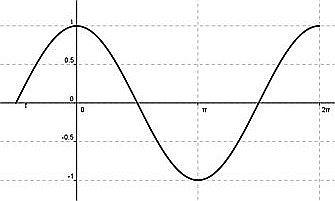
B) grafico di y=|cosx| 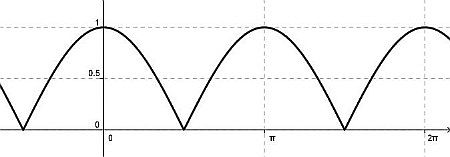
C) grafico di y = √x: 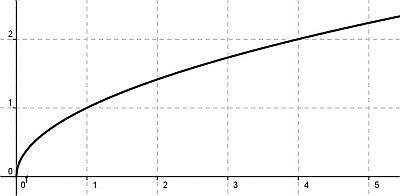
D) grafico finale
Il grafico finale ha lo stesso andamento del grafico di y=|cosx| perché la composizione con la funzione crescente y = √x non cambia la monotonia di y=|cosx|; restano fisse le ordinate quando valgono 1 oppure 0 (√1 = 1 e √0 = 0), mentre cambiano in tutti gli altri punti del dominio.
Chiamata F(x) una funzione integrale di ![]() per x
per x ![]() [-π/2, 3π/2], si ottengono informazioni interessanti: il segno della funzione f(x) fornisce indicazioni sulla monotonia di F(x), la monotonia della funzione f(x) fornisce indicazioni sulla concavità di F(x).
[-π/2, 3π/2], si ottengono informazioni interessanti: il segno della funzione f(x) fornisce indicazioni sulla monotonia di F(x), la monotonia della funzione f(x) fornisce indicazioni sulla concavità di F(x).
Tutto si gioca sull’identità f(x) = DF(x), cioè di F si conosce la derivata prima (f(x)) e la derivata seconda (Df(x)). Fissando il passaggio per un punto (x0,y0) del piano, si identifica una particolare funzione integrale, di cui si può fare un grafico qualitativo, anche quando non si voglia o non si sappia integrare f(x).
Funzione reciproco: dal grafico di f(x) al grafico di 1/f(x)
La funzione 1/f(x) è composta in questo modo: x → f(x) = t → y = 1/t dove la funzione y = 1/t è decrescente quando t è positiva, oppure quando t è negativa e non è definita in t = 0 . Possiamo concludere che se (in un intervallo U dove f(x) è definita e non nulla) f(x) cresce, allora 1/f(x) decresce e viceversa.
Esempio 1
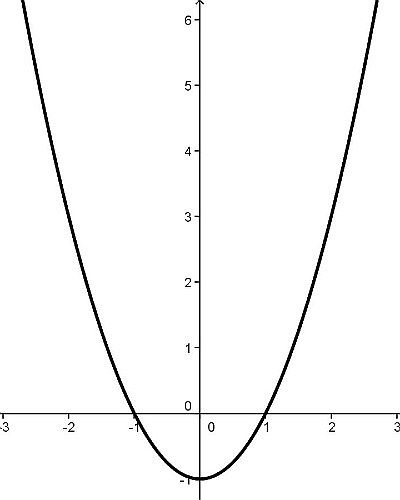 y = x2 – 1, parabola con concavità verso l’alto, definita per ogni x reale, pari, il suo asse è l’asse y, il vertice è V (-1;0), le intersezioni con l’asse x hanno ascissa x = 1 e x = -1 (vedi grafico a sinistra).
y = x2 – 1, parabola con concavità verso l’alto, definita per ogni x reale, pari, il suo asse è l’asse y, il vertice è V (-1;0), le intersezioni con l’asse x hanno ascissa x = 1 e x = -1 (vedi grafico a sinistra).
Passiamo al reciproco, cercando di dedurlo. y = 1 /(x2 – 1), è una funzione composta: x → t = x2 -1 → y = 1/t; definita quando (x2 – 1) ≠ 0, quindi per x ≠ 1 e x ≠ -1 è una funzione pari: è simmetrica rispetto all’asse y; per fare il suo grafico non c’è bisogno di introdurre il calcolo di limiti, ma basta ragionare sulle immagini. Suddividiamo il dominio in intervalli in cui y = 1/(x2–1) sia continua e prevediamo la monotonia.
Suddividiamo il dominio in intervalli in cui y = 1/(x2–1) sia continua e prevediamo la monotonia.
Chiamiamo f(x) la parabola e 1/f(x) il reciproco (vedi grafico riportato a destra).
Per x < -1: f(x) decresce → 1/f(x) cresce; l’immagine di f(x) è (0, +∞) e l’immagine di 1/f(x) è la stessa.
Per -1 < x < 1: f(x) decresce fino a x = 0 e poi cresce → 1/f(x) cresce fino a x = 0 e poi decresce; l’immagine di f(x) è l’intervallo -1 ≤ y < 0 e l’immagine di 1/f(x) è y ≤ -1.
Per x > 1: f(x) cresce → 1/f(x) decresce, immagine di f(x): 0 < x < +∞, resta la stessa per 1/f(x).
Esempio 2
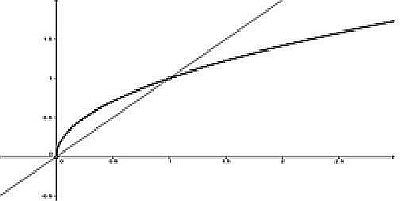 y=1√x : il grafico si deduce da quello di x = y2 (considerata per y > 0), parabola che ha come asse l’asse x; il grafico incontra in P(1,1) la retta y = x, punto che si conserva nel reciproco (vedi grafico riportato a sinistra).
y=1√x : il grafico si deduce da quello di x = y2 (considerata per y > 0), parabola che ha come asse l’asse x; il grafico incontra in P(1,1) la retta y = x, punto che si conserva nel reciproco (vedi grafico riportato a sinistra).
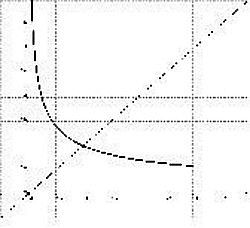 Passiamo al grafico del reciproco.
Passiamo al grafico del reciproco.
- y=1/√x : è una funzione composta: x → t = √x → y = 1/t (si noti che t ≠ 0 → √x ≠0 → x ≠ 0)
- 0 < x ≤ 1 → 0 < √x ≤ 1 → 1/√x ≥ 1
- x ≥ 1 → √x ≥ 1 → 0 < 1/√x ≤ 1
La monotonia viene cambiata, anche il grafico di 1/f(x) passa per il punto P(1,1). (vedi grafico riportato a destra)
Dal grafico di y = f (x) , dedurre il grafico di y= f2(x)
Esempio 1
Dal grafico della funzione y = 1-x2; deduciamo il grafico di y = (1-x2)2 .
Passando da f(x) a f2(x) si conservano gli zeri, cioè le intersezioni con l’asse x; sono entrambe funzioni pari; l’ordinata della funzione quadrato è sempre positiva (ed è nulla in x = 1 e x = -1); è una funzione composta in questo modo: x → t = 1–x2 → y = t2;
Monotonia:
x < -1: t(x) cresce, trasforma (-∞, -1) in (-∞, -1), il primo è letto sull’asse x e il secondo sull’asse y;
in (-∞, -1) y(t) decresce, quindi la f(x) composta decresce;
-1 < x ≤ 0: t(x) cresce, trasforma (-1,0] in (0,1];
in (0,1] y(t) cresce, quindi la f(x) composta cresce;
si completa il grafico per simmetria rispetto all’asse y. Il grafico è riportato accanto a quello della funzione dell’esempio seguente.
Esempio 2
Dal grafico della funzione y = sinx deduciamo il grafico di y = (sinx)2 = sin2x.
In virtù della periodicità (T = 2π) consideriamo la funzione seno nell’intervallo [-π,π]: la funzione quadrato (sin2x) è sempre positiva, la composizione è analoga a quella della funzione precedente: x → t = sinx → y = t2;
Monotonia: dove t2 è decrescente (ascissa negativa), cambia la monotonia della prima funzione, dove t2 è crescente (ascissa positiva), lascia invariata la monotonia della prima funzione. Ricordiamo che la funzione t2 viene calcolata sull’immagine di sinx, quindi dove sinx è negativa c’è cambiamento, dove sinx è positiva non c’è cambiamento; scriviamolo con disuguaglianze:
x [-π,-π/2] → t ![]() [-1,0]: t(x) decresce, sinx decresce, f(x) composta cresce
[-1,0]: t(x) decresce, sinx decresce, f(x) composta cresce
x [-π/2,0] → t [-1,0]: t(x) decresce, sinx cresce, f(x) composta decresce
x ![]() [0,π/2] → t
[0,π/2] → t![]() [0,1]: t(x) cresce, sinx cresce, f(x) composta cresce
[0,1]: t(x) cresce, sinx cresce, f(x) composta cresce
x ![]() [π/2,π] → t
[π/2,π] → t ![]() [0,1]: t(x) cresce, sinx decresce, f(x) composta decresce
[0,1]: t(x) cresce, sinx decresce, f(x) composta decresce
Ecco i grafici delle due funzioni y = (1–x2)2 e y = (sinx)2 = sin2x:
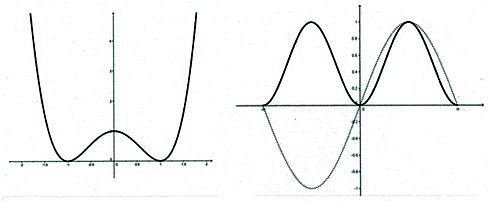
A sinistra il grafico della funzione: y = (1-x2)2 ; a destra il grafico della funzione: sin2x
Si noti che, a vista, sembra che ci sia eguaglianza tra grafici: y = 1–x2 e il suo quadrato per x ![]() [-1,1], y = sinx e il suo quadrato per x [0,π]. Ma questo non è vero, perché anche se l’andamento coincide, le ordinate sono diverse: due funzioni coincidono in un intervallo solo quando per ogni x di quell’intervallo hanno la stessa ordinata.
[-1,1], y = sinx e il suo quadrato per x [0,π]. Ma questo non è vero, perché anche se l’andamento coincide, le ordinate sono diverse: due funzioni coincidono in un intervallo solo quando per ogni x di quell’intervallo hanno la stessa ordinata.
Prendiamo un esempio dalla trigonometria. 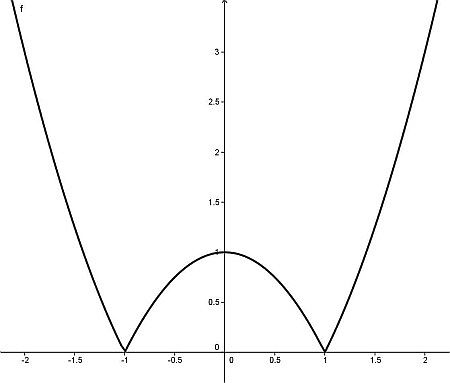 La formula sin2x = 2 sinx cosx vale per ogni valore reale di x ed è un’identità. Questa uguaglianza comporta che sul piano cartesiano coincidano i grafici delle due funzioni y = sin2x e y = 2 sinx cosx .
La formula sin2x = 2 sinx cosx vale per ogni valore reale di x ed è un’identità. Questa uguaglianza comporta che sul piano cartesiano coincidano i grafici delle due funzioni y = sin2x e y = 2 sinx cosx .
Il grafico della funzione y = |1-x2| (riportato qui a sinistra) ha qualche somiglianza visiva con quello di y = (1-x2)2, coincidono gli zeri e la monotonia, ma mentre la funzione quadrato è sempre derivabile, con tangente orizzontale in x = 1 e x = -1, la funzione modulo non è derivabile in x = -1 e x = 1. Una ulteriore somiglianza è che entrambe hanno un minimo sia in x = -1 che in x = 1.
Anna Paola Longo
(Svolge attività di ricerca e formazione sull’apprendimento della Matematica – Politecnico di Torino)
© Pubblicato sul n° 43 di Emmeciquadro
