Partendo da un’analogia tra il campo elettromagnetico e quello gravitazionale, l’autore mostra come dalle equazioni di Einstein della relatività generale derivi la previsione delle onde gravitazionali. Quindi descrive l’esperimento, basato su un interferometro gravitazionale di Michelson, che ha rivelato l’esistenza delle onde, commentando i risultati.
Una trattazione molto interessante, condotta con rigoroso formalismo matematico, che potrà risultare impegnativo per molti lettori, ma necessario per non ridurre la portata della teoria einsteiniana.
La consultazione di un precedente articolo, L’eredità scientifica di Einstein, Emmeciquadro n.61 – Giugno 2016, dello stesso autore, può agevolare una piena comprensione di questa importante conquista teorica e oggi anche sperimentale.
Non c’è stato modo migliore di celebrare il centenario della Relatività Generale, che confermare l’esistenza delle onde gravitazionali!
La loro osservazione diretta risale al 14 settembre 2015, mentre l’annuncio ufficiale è stato dato solo l’11 febbraio scorso. L’attesa della loro scoperta è stata lunga. D’altra parte, le equazioni del campo gravitazionale, trovate da Einstein nel novembre 1915, non lasciavano dubbi.
Presupposti
L’introduzione della gravità nell’elemento infinitesimo della metrica spazio-temporale, era stata un’idea degna della genialità di Albert Einstein (1879-1955). Con riferimento all’articolo precedente (L’eredità scientifica di Einstein, Emmeciquadro n.61 – Giugno 2016), ricordiamo che il potenziale gravitazionale 
era stato inserito sia nella parte temporale che in quella spaziale dell’elemento infinitesimo dello spazio-tempo.
Come sottolineato da Einstein, bastava quindi cambiare il sistema delle coordinate di riferimento per poter ottenere l’inserimento della gravità [Einstein, 1916, pg.511].
Le conseguenze, già considerate, sono davvero notevoli:
La presenza di una massa modifica la metrica dello spazio-tempo;
Anche un fotone, in un campo curvato dalla gravitazione, flette la sua traiettoria;
Un qualunque corpo dotato di massa può quindi causare effetti di lente gravitazionale.
Rimane poi l’ultima, oggetto specifico del presente articolo:
Movimenti di masse causano increspature nello spazio-tempo che si possono propagare sotto forma di onde gravitazionali (Figura 1).
Figura 1
I movimenti di masse, nel loro reciproco avvicinamento, causano vibrazioni dello spazio-tempo in grado di propagarsi come onde gravitazionali.
La costruzione originale dell’elemento spazio-temporale, non era tuttavia sufficiente, come abbiamo visto: occorreva trovare la relazione esatta fra le sorgenti del campo gravitazionale e le deformazioni della metrica procurate dalla loro presenza.
Queste sarebbero state le equazioni del campo gravitazionale: in linea di principio, bastava costruire l’analogo di ciò che James C. Maxwell (1831-1879) aveva già fatto per il campo elettromagnetico (E-H).
In tale deduzione analogica, appare immediata la presenza delle onde gravitazionali, come conseguenza delle equazioni di campo, alla stregua di quelle elettromagnetiche, conseguenza delle equazioni di Maxwell.
Il campo gravitazionale e quello elettromagnetico
Deduzione delle equazioni gravitazionali per analogia con quelle di Maxwell
L’intensità del campo elettrico 
, e magnetico 
sono date, rispettivamente, mediante il potenziale elettrico scalare ed il potenziale vettore 
nel modo seguente:
Nello spazio di Minkowski, dove tre coordinate sono spaziali e reali 
mentre la quarta è temporale e immaginaria, ict (i=unità immaginaria, c=velocità della luce), ogni punto quadridimensionale è dato da:
essendo (µ = 1,2,3,4).
In questo spazio si costruisce un vettore potenziale a quattro componenti, di cui tre sono reali 
e la quarta è immaginaria 
In modo sintetico scriveremo questo tetrapotenziale come:
Ed esprimeremo con esso1 le equazioni di Maxwell, nel modo seguente:
Dove viene definito un nuovo tetravettore, 
fatto con, 
= densità elettrica spaziale e 
densità superficiale di corrente sulla sezione S2.
Il significato fisico profondo delle equazioni di Maxwell nei potenziali, è quello di legare la descrizione del campo (E-H), mediante Aµ, in grado di descrivere completamente il campo (E-H) sia nella parte elettrica che magnetica, alle sue sorgenti, cioè le cariche e le correnti: 
L’analogo deve avvenire per il campo gravitazionale.
Quest’ultimo deve essere descritto dall’analogo del tetrapotenziale, Aμ, costruito con il potenziale gravitazionale, ϕ, e comparire a primo membro. Sapendo che, ϕ, è già dentro all’elemento della metrica spazio-temporale, gμν, (μ,ν = 1,2,3,4 ) che è un tensore3 (il tensore metrico), ci si aspetta che ad □ Aμ corrisponda un □ gμν.
A secondo membro devono esserci le sorgenti della gravità, l’analogo di jμ, dentro un tensore energia-impulso, Tμν, contenente tutti i contributi alla massa da parte della materia, sia diretti, come la densità, sia trasformabili mediante: E = mc2, vale a dire tutte le forme di energia della materia, interna (per esempio la pressione) o di movimento (energia cinetica).
Pertanto la sequenza analogica per transitare dalle equazioni di Maxwell a quelle di Einstein sarà:
È interessante notare che, in approssimazione di campo gravitazionale debole e stazionario 
nel limite dello spazio piatto di Minkowski e nel sistema di riferimento solidale con il campo in movimento, le equazioni di Einstein si riducono all’equazione familiare di Poisson:
∇2 ϕ = 4πGρ
Che lega appunto il campo ϕ alla sua sorgente, la densità di materia ϱ.
Previsione delle onde gravitazionali dall’analogia con quelle di Maxwell
Non appena l’analogia, appena descritta, diviene lecita, immediatamente è evidente l’esistenza delle onde gravitazionali. Infatti, come nel campo (E-H) la natura stessa delle equazioni implica la propagazione delle onde elettromagnetiche (basti pensare che, lontano dalle sorgenti, quindi jμ = 0, le equazioni di Maxwell diventano proprio le equazioni di propagazione di d’Alembert) altrettanto, le equazioni così dedotte per il campo gravitazionale, analoghe a quelle di Maxwell, implicano la propagazione delle onde gravitazionali.
C’è, tuttavia, una differenza enorme fra la forza elettromagnetica e quella gravitazionale. La possiamo capire, confrontando l’intensità di queste due forze (in variabili adimensionali).
Vi è un fattore di diminuzione di circa 10-37 fra le due, a sfavore della forza gravitazionale.
Questo spiega, immediatamente il motivo della difficoltà di rilevazione delle onde gravitazionali rispetto a quella delle onde elettromagnetiche.
Limiti dell’analogia
L’analogia considerata fra il campo elettromagnetico e quello gravitazionale rimane molto proficua per la comprensione del senso delle equazioni di Einstein, tuttavia essa possiede dei limiti legati alla diversa natura dei due campi.
Sostanzialmente, mentre le equazioni di Maxwell sono lineari, quelle originali di Einstein non lo sono5. Inoltre le prime sono vettoriali, le seconde sono invece tensoriali.
L’analogia fra i due tipi di equazioni, diventa significativa soltanto quando le equazioni di campo gravitazionale si possono linearizzare, vale a dire nel vuoto o con la presenza di materia, ma solo sotto particolari condizioni.
Riassumendo le proprietà delle onde gravitazionali linearizzate, sono [Hartle, Cap.16, pag.332] le seguenti: si propagano con la velocità della luce; sono trasversali; hanno due stati indipendenti di polarizzazione4; possono essere evidenziate dal moto relativo di masse test mediante interferometro.
In realtà la trattazione teorica è più complessa di quella basata sull’analogia (si veda l’Approfondimento) ed è consigliata a chi ha già una conoscenza specifica dell’argomento.
Rivelazione dell’evento e sua interpretazione
L’apparato osservativo
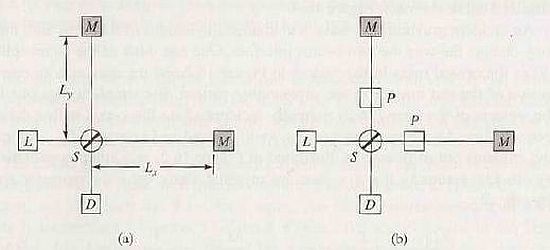Figura 2: Schema dell’interferometro gravitazionale di Michelson
In riferimento alla Figura 2, le masse test, sospese verticalmente, sono: una in S, dove è alloggiato il beam splitter che divide in due parti il fascio laser proveniente da L, due in M, dove sono alloggiati i due specchi alla fine dei due bracci Lx, Ly (a).
Piccole differenze nella lunghezza dei due bracci, sono evidenziate dalla figura d’interferenza sul detector D. L’aggiunta dei due specchi P in (b), hanno l’effetto di aumentare la lunghezza dei bracci e quindi la sensibilità dell’interferometro [Hartle, 2003, pag. 339].
Con riferimento alla Figura 2 (a), supponiamo che le due masse test siano sospese verticalmente in modo da potersi muovere liberamente in senso orizzontale, corrispondente al piano della figura.
Una massa è in S (porta il beam splitter), l’altra in M (porta lo specchio) definendo il termine del braccio Lx, oppure Ly. Sia L* la distanza fra ciascuna delle due coppie di masse (S,M), sul piano z=0 perpendicolare alla direzione di propagazione.
Un’onda incidente gravitazionale cambierà la lunghezza dei bracci.
Se prendiamo in esame lo stato di polarizzazione «+», e assumiamo che i due bracci dell’interferometro, che cade liberamente (Principio di Equivalenza, vedi L’eredità scientifica di A. Einstein, Emmeciquadro n.61 – Giugno 2016) siano orientati secondo gli assi x-y, il braccio Lx si contrarrà e si espanderà, mentre quello Ly si espanderà e si contrarrà con fase diversa (vedi Figura 7). Precisamente:
L’ampiezza «a» e la pulsazione «ω» possono essere misurate monitorando la figura d’interferenza sul rivelatore D.
I rapporti δLi/Li, (i = x,y) sono chiamati, mutuando un termine dalla teoria dell’elasticità, strain, sforzo prodotto dall’onda gravitazionale e risultano essere, per rivelatori alla distanza della Terra, dell’ordine di 10-21.
Per l’interferometro LIGO con bracci di 4 km, le differenze di lunghezza coinvolte sono dell’ordine di 10-18 m.
L’evento osservato
L’evento, GW150914 (evidenziato in data 14 settembre 2015, dentro la sigla), è stato captato dalle due antenne gravitazionali LIGO (Figura 3).
Le antenne LIGO e VIRGO
Si tratta di due interferometri, ciascuno come quello descritto in Figura 2, posti uno a ovest degli Stati Uniti, Hanford, (Washington), l’altro ad est, Livinston (Louisiana) (Figura 3).
Sono analoghi a VIRGO collocato a Cascina (Pisa) (Figura 4) che era, alla data dell’evento, in manutenzione. I due interferometri (H1, L1), hanno captato i segnali riportati in Figura 5 (pannelli superiori), ricostruiti e confrontati con quelli previsti dal calcolo numerico relativistico (pannelli inferiori).
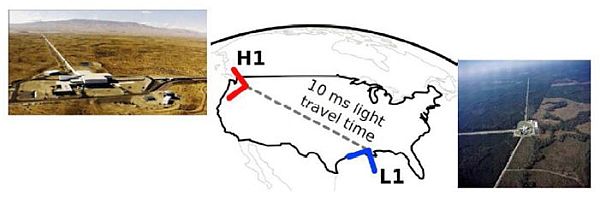Figura 3
LIGO=Laser Interferometer Gravitational-Wave Observatory. I due interferometri negli Stati Uniti uno ad ovest, Hanford, (Washington), H1, l’altro ad est, Livinston (Louisiana), L1, con bracci perpendicolari di 4 km. Il tempo di percorrenza della distanza fra i due, per un segnale che viaggi alla velocità della luce, è di circa 10 ms [Zendri, 2016].
Figura 4
Interferometro VIRGO per rilevare onde gravitazionali, simile ai due LIGO americani (Figura 3), con bracci perpendicolari di 3 Km, in località Cascina (Pisa).
I segnali captati
I segnali captati dai due interferometri (H1,L1), il 14 settembre 2015, sono rappresentati nei pannelli superiori di Figura 6. La loro sovrapponibilità, nel pannello di destra, tenuto conto della differenza di ricezione fra le due antenne distanti, in termini di tempo luce, circa 10 ms, garantisce trattarsi del medesimo evento.
La ricostruzione, a partire dalla relatività (pannelli inferiori della Figura 6) garantisce che si tratti effettivamente di onde gravitazionali.
Il loro effetto sui due bracci dell’interferometro che le riceve, è visualizzato in Figura 7.
Per semplicità viene considerato solo uno stato di polarizzazione «h+» che «strizza» o «stira» i due bracci in modo sinusoidale, con diverso sfasamento, dando una ragione immediata delle variazioni della figura d’interferenza sul detector D.
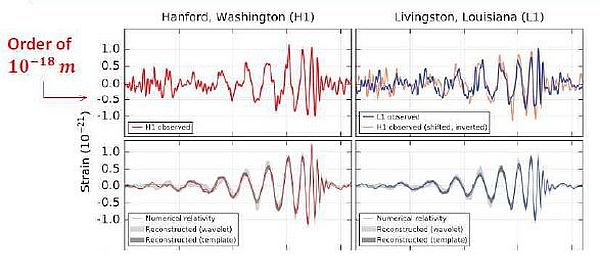Figura 5
I segnali captati dalle due antenne gravitazionali (H1,L1) (pannelli superiori). In L1 il segnale ricevuto da H1, è sovrapposto per confronto, traslato di circa 10 ms, causa la distanza fra i due ricevitori. La ricostruzione teorica e il confronto con le ricezioni sono mostrati nei pannelli inferiori [Zendri, 2016].
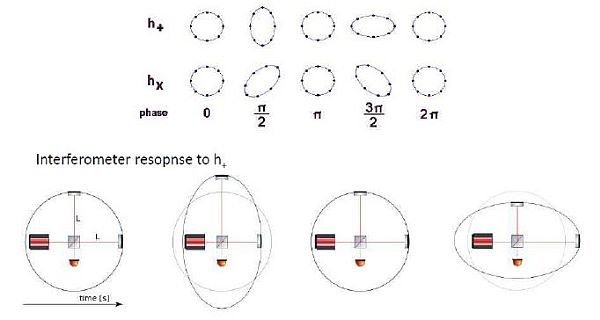Figura 6
Effetto dell’onda gravitazionale, con stato di polarizzazione «h+» (in alto), sui due bracci, L_(x )(orizzontale), L_(y )(verticale), di ciascun interferometro, in funzione del tempo, per un periodo di oscillazione. I due bracci dell’interferometro si contraggono e si espandono con fase diversa (Eq.4.1).
L’interpretazione
Le caratteristiche dell’evento sono interpretabili con la coalescenza di due BH (black hole, Figura 8), vale a dire la fase iniziale di spiraleggiamento orbitale (orbital inspiral), il loro fondersi (merger) e infine la trasformazione del sistema binario in un unico black hole.
Una rappresentazione pittorica suggestiva è data in Figura 8.
Le caratteristiche del merger sono sintetizzate nella Tabella in Figura 9. Particolarmente rilevante è l’energia che va in onde gravitazionali, pari a circa 3 MO (MO = massa del Sole)
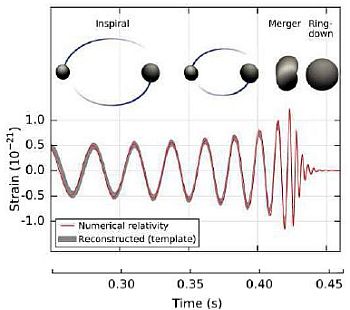
Figura 7 [a sinistra]
Interpretazione delle variazioni di frequenza dello strain gravitazionale in funzione del tempo. Si tratta delle fasi successive di un fenomeno di coalescenza di due buchi neri (BH) (v. testo).
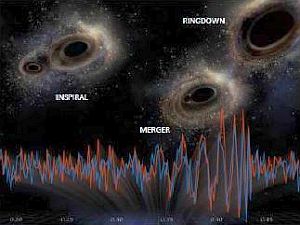
Figura 8 [a destra]
Rappresentazione pittorica del merger di due BH come interpretazione dei dati di Figura 7.
Figura 9 [a sinistra]
Tabella riassuntiva dei dati che caratterizzano il merger di due BH descritto dal trend delle onde gravitazionali di Figura 8. L’energia corrispondente è enorme [Zendri, 2016].
Frequenze e λ tipiche
Come abbiamo detto, i movimenti di masse causano increspature nello spazio-tempo, descritte dai termini hμν, che si propagano come onde. Per poter capire perché l’aumento nel tempo della loro frequenza corrisponda all’avvicinamento dei due oggetti (BH) causando alla fine la loro coalescenza, consideriamo due corpi di massa M che si muovono l’uno rispetto all’altro e vogliamo ricavare frequenza e lunghezza d’onda del moto ondoso prodotto dal loro reciproco movimento.
Con riferimento alla Figura 10, il problema a due corpi di massa M si riconduce a quello di una massa ridotta μ, pari a M/2, orbitante attorno ad un punto fisso a distanza 2R dove è concentrata la massa totale del sistema, Mtot, pari a 2M.
Nel sistema di riferimento del centro di massa [Università degli Studi di Cagliari], vale l’equazione differenziale:
essendo L il momento angolare rispetto al baricentro e r la distanza fra le due masse orbitanti attorno al comune baricentro.
Nel caso di orbita circolare, l’equazione diventa:
Sostituendo ad r=2R (vedi Figura 10) e semplificando, si ottiene infine:
essendo Ω la frequenza orbitale6.
La velocità V rispetto al baricentro e la frequenza orbitale sono quindi date da:
La frequenza e la lunghezza d’onda, risultano quindi, rispettivamente:
a cui si vede che, come la distanza R fra le due masse fissate si riduce, come quando avviene il merger (Figura 7), la frequenza ν dell’onda aumenta mentre la lunghezza d’onda λ cala. A parità di altre condizioni, lo stesso effetto si ottiene aumentando la massa M.
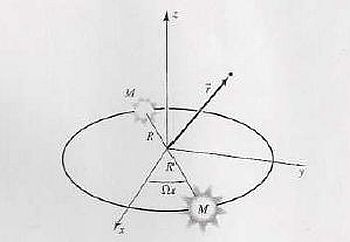Figura 10
Sistema binario con due oggetti di uguale massa M [Hartle, 2003, pg. 503]. Le orbite sono circolari, sul piano x-y, con velocità angolare Ω. L’onda gravitazionale viene emessa lungo una generica direzione 
Confronto fra sistemi binari
Per esemplificare gli sviluppi esposti, consideriamo innanzitutto il sistema binario PSR 1913+16 scoperto da Russell A.Hulse (1950- ) e Joseph H.Taylor (1941- ) nel 1974 e che meritò loro il Premio Nobel nel 1993 [Hartle, 2003, pag.250].
Si tratta di una pulsar binaria con massa di circa 1.4 MO sia della pulsar che del compagno invisibile. Il periodo orbitale è circa Pb = 7h 45m ed è stato monitorato per circa 30 anni con il radio telescopio di Arecibo.
La sua diminuzione ha fornito una eccellente prova dell’esistenza di radiazione gravitazionale dovuta al movimento rapido della pulsar nel forte campo gravitazionale del suo compagno invisibile e, nel contempo, una profonda conferma della teoria della relatività [Taylor & Weisberg, 1982]. Usando le formule precedenti, per un raggio orbitale R ≃ 106 km la frequenza dell’onda gravitazionale, risulta ν = 7∙ 10-5 Hz (vedi Tabella in Figura 11).
Le stesse formule forniscono, per il sistema GW150914, una frequenza molto più alta, ν ≃ 117 Hz usando un valore di R ≃ 200 km ed una massa M ≃ 30 MO (vedi Tabella e pannello superiore in Figura 11).
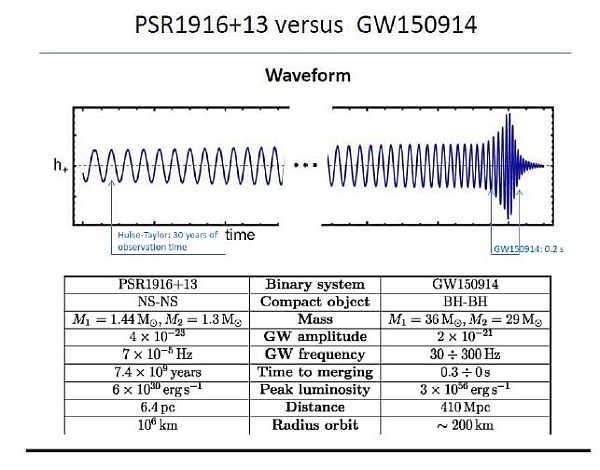Figura 11
Confronto fra sistemi binari (vedi testo). Le diverse frequenze delle onde gravitazionali nei due sistemi, sono ricavabili dalle equazioni sopra esposte [Zendri, 2016].
Localizzazione della sorgente e probabilità di falso allarme
La localizzazione della sorgente è mostrata nel plot di Figura 12, in termini di aree di probabilità, espresse in ascensione retta (RA, orizzontale) e declinazione (DEC, verticale) [Vedovato, 2016].
Con solo due rivelatori, la localizzazione della sorgente non è molto accurata: 590 deg2 al 90% di probabilità che si riducono a 140 deg2 al 50% di probabilità.
Da notare che:
l’area iniziale (circa 600 deg2) determinata dai dati L1 e H1, si ridurrebbe di circa un fattore 30, una volta che si usi anche Virgo (Figura 13) [Abbott et al., 2016], [Zendri(a), 2016].
La probabilità che si tratti di un falso allarme è minore di 2·10-6 .
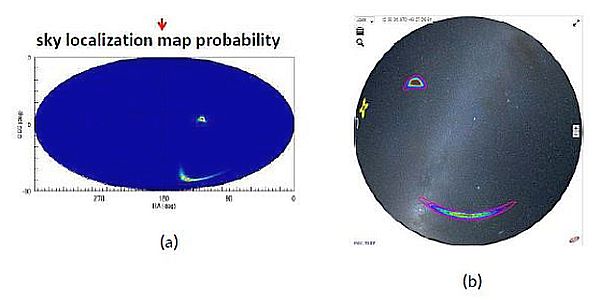Figura 12
Aree di localizzazione della sorgente in ascensione retta (RA, orizzontale) e declinazione (DEC, verticale) (a). La probabilità decresce verso l’interno a partire dal contorno più esterno pari al 90%, (b) [Vedovato, 2016; Zendri(a), 2016].
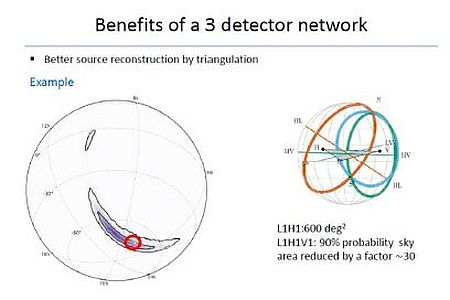Figura 13
y Localizzazione della sorgente usando anche VIRGO [Zendri, 2016]. L’area iniziale determinata dai soli dati L1 e H1, si ridurrebbe di circa un fattore 30 (zona in rosso).
Conclusioni
Mi sono chiesto se si potesse scorgere nell’evento delle onde gravitazionali, qualche significato riconducibile a un ambito oltre a quello della Scienza. La frase, che già è stata la linea guida di tutta la prima trattazione dell’opera scientifica di Einstein: «quello che c’è, nel mondo, di eternamente incomprensibile, è che esso sia comprensibile», mi pare possa essere anche la chiusura di questa seconda.
C’è nell’Universo una tensione a rivelarsi. L’Universo «desidera» parlare di se stesso; dall’abisso di circa 1.2 miliardi di anni luce, l’evento delle onde gravitazionali risuona ora da noi con un eco con cui il Creato «desidera» mettersi in relazione con l’Uomo che l’osserva.
La relazione, è il tratto caratterizzante la Trinità, così come Cristo ce lo ha rivelato. Ma la tensione alla relazione è ciò che caratterizza l’Amore. All’interno della dinamica dell’Amore ci viene insegnato che, mentre «Dio Padre ….sembra esprimere solo la disponibilità a dare, a darsi…Dio Figlio sottolinea che è divino il riavere… » [Sartori, 2003, pag.42].
Dal Suo capolavoro, l’Artista stesso riceve, è l’eco del Creato. Tuttavia c’è un interlocutore privilegiato in questo dialogo d’Amore, qualcuno a cui offrire il Creato stesso.
«Egli fabbrica con l’Universo che è fabbricato e traccia linee continuamente nuove e libere nel Suo progetto, in un divenire mosso dall’idea finale…del dono all’Uomo, da cui nasce la Bellezza» [Secco, 2016].
Ecco allora perché a questo qualcuno deve essere comprensibile il mondo, perché egli è fatto «a immagine e somiglianza Sua» per la condivisione gioiosa del Creato.
Dalle grandi Religioni Tradizionali, ci viene un insegnamento rilevante, ricordatoci da Dallaporta [Dallaporta 2000, pag.67]. Secondo un hadith (parola del Profeta) islamico: «Ero un tesoro nascosto; ho voluto essere conosciuto, ed ho creato il mondo».
Questa è l’unica «necessità» che Dio ha, quella di creare. Si tratta di una esigenza come Sommo Bene e costituisce, come già messo in luce da Sant’Agostino, l’essenza stessa del Reale.
Luigi Secco
(Dipartimento di Fisica e Astronomia, Università di Padova)
Note
Ricordiamo che il simbolo di d’Alembert è:
Tale da fornire, con la sua integrazione, la corrente di conduzione
Vale a dire una matrice, in questo caso 4X4
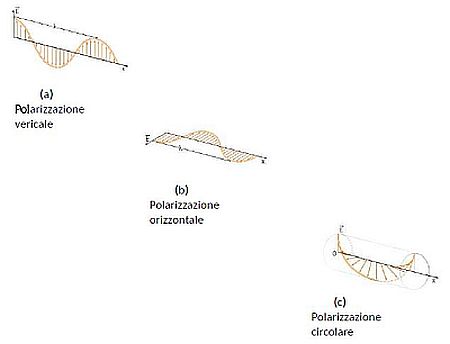
Polarizzazione delle onde elettromagnetiche
Ci riferiamo all’oscillazione del vettore campo elettrico
di un’onda elettromagnetica (trasversale); poiché il campo magnetico è sempre perpendicolare al campo elettrico e ad esso proporzionale, è sufficiente riferirsi a quest’ultimo (vedi Figura).
Polarizzazione verticale (a), orizzontale (b), circolare (c) di un’onda elettromagnetica.Se
oscilla sempre su un piano verticale, l’onda è polarizzata verticalmente, se oscilla sempre su un piano orizzontale, l’onda è polarizzata orizzontalmente. Se invece ruota attorno alla direzione di propagazione, l’onda è polarizzata circolarmente.
Il vettore ruota spostandosi dal piano verticale a quello orizzontale, per tornare poi a quello orizzontale, descrivendo con la sua punta, una circonferenza con velocità angolare ω (in senso orario o antiorario).
Poiché ogni vettore che giace sul piano perpendicolare alla direzione di propagazione può essere scomposto in due componenti, una orizzontale, Ex , ed una verticale, Ey , una qualunque onda polarizzata può essere ottenuta come opportuna sovrapposizione di un’onda polarizzata orizzontalmente e di un’onda polarizzata verticalmente. Si ottiene così la polarizzazione circolare (in senso orario o antiorario) quando le due componenti oscillanti, Ex , Ey , sono sfasate fra loro di ±π/2 .
Nel caso in cui lo sfasamento fra le due componenti sia in modulo diverso da π/2 (o suoi multipli dispari), si ottiene la polarizzazione ellittica, in cui la punta di descrive sul piano di oscillazione, un’ellisse (in senso orario o antiorario).Significa che implicano derivate di qualunque ordine ma non solo di primo grado
Rimane invariata passando dal sistema con origine nel baricentro a quello con origine in una delle due masse
Note Bibliografiche
Abbott, B.P., et al., 2016, Physical Review Letters, 116, 061102.
Dallaporta, N., Semi del Verbo nelle grandi Religioni Tradizionali, Libreria Editrice Gregoriana, 2000.
Drago, M., Corso di Dottorato del XXII ciclo, Università di Padova,www.pd.infn.it
Einstein, A., Memoria del 1916, in Cinquant’anni di Relatività, autori vari, pag.511, Edizioni Giuntine & Sansoni Editore, 1955
Hartle, J.B., Gravity, An Introduction to Einstein’s General Relativity, Addison Wesley Edition,2003.
L.Sartori, Per una metafisica dell’Amore, Studia Patavina, 50, 25, 2003.
Secco, L., Ci hai dato il cielo e le chiare stelle, in corso di pubblicazione.
Straneo, P., in Cinquant’anni di Relatività, autori vari, pag. 29, Edizioni Giuntine & Sansoni Editore, 1955.
Taylor, J.H., Weisberg, J.M., Ap.J., 1982, 253, 908-920.
Vedovato, G., Seminario Univ.Padova, 19 febbraio, 2016. www.virgo.lnl.infn.it
Zendri, J.P., Seminario Univ.Padova, 19 febbraio, 2016. www.virgo.lnl.infn.it
Zendri(a), J.P., Seminario Scuole, marzo, 2016. www.virgo.lnl.infn.it
© Pubblicato sul n° 62 di Emmeciquadro
