In questo terzo articolo dedicato alla teoria relativistica di Sergio Serapioni, l’autore riprende in esame lo spazio a cinque dimensioni in cui si sviluppa la teoria, per mostrare un nuovo concetto di tempo e la riduzione di tutti i moti a rotazioni nello spazio a cinque dimensioni.
Da qui, in modo un po’ imprevedibile, deriva l’esistenza della materia oscura, e dell’energia oscura, nelle proporzioni, rispetto alla materia ordinaria, corrispondenti ai dati sperimentali attuali.
Abbiamo già avuto modo di introdurre la teoria di spazio e tempo sviluppata dall’Ingegner Sergio Serapioni nel corso della sua quarantennale attività (si veda ad esempio: Il sorriso dell’Ingegnere per i primi risultati del Satellite Planck, Emmeciquadro n. 49 – Giuno 2013 e Macro e micro cosmo nell’Universo di Serapioni, Emmeciquadro n. 57 – Giugno 2015). Rimandiamo pertanto il lettore interessato ai suddetti articoli, qui ci basti ricordare i punti salienti della teoria. Essa prende le mosse dai lavori del matematico romano Luigi Fantappiè, grande amico di Enrico Fermi.
La questione fondamentale è una visione unitaria della realtà fisica che, seguendo appunto Fantappiè, viene immaginata attraverso un’opportuna geometrizzazione delle fisica. In questo processo si riesce a comprendere in maniera naturale il concetto di tempo che ancora oggi nella fisica teorica porta con sé questioni irrisolte.
Ci basti per esempio immaginare il tempo come qualcosa che c’è fin dall’inizio e che viene incluso in una teoria come semplice parametro che indicizza l’evoluzione temporale dello stato di un sistema. D’altro canto si può pensare al tempo come a un qualcosa che «emerge» dalla teoria stessa sotto opportune condizione e ne è pertanto una caratteristica fondamentale.
Su queste due visioni differenti del tempo sono costruite le due teorie fisiche di più grande successo dell’ultimo secolo: la relatività generale di Einstein e la meccanica quantistica. Nella prima abbiamo infatti una teoria senza alcuna struttura di tempo definita: è a tutti gli effetti una teoria indipendente da un background, da uno scenario, da un palcoscenico in cui gli eventi fisici «recitano». Per contro la meccanica quantistica necessita di una grandezza, il tempo, per descrivere come lo stato s di un sistema S cambi.
Il tentativo di una riconciliazione di queste due apparentemente discordanti visioni dell’Universo è uno degli sforzi della moderna Fisica teorica.
L’Universo, la realtà tutta è una e pertanto si ritiene debba esserci una teoria che descriva questa unità. Tuttavia non è detto che questa unità sia indagabile in questo senso e che quindi una tale teoria sia effettivamente a «portata di scienziato».
La teoria di Serapioni: un nuovo concetto di tempo
In questo senso mi pare interessante analizzare e studiare il lavoro di Serapioni che propone una teoria con un nuovo approccio al concetto di tempo. Esso è pensato come l’esito di un movimento (più precisamente una rotazione).
Occorre introdurre a questo punto uno concetto matematico importante anche da un punto di vista fisico: la nozione di gruppo. Un gruppo in matematica è un insieme di elementi dotato di un’operazione che permette di combinare due elementi qualsiasi del gruppo per ottenere un altro elemento del gruppo e che soddisfa alcune condizioni (detti assiomi) quali la chiusura (operando su elementi del gruppo si ottengono sempre elementi del gruppo stesso), l’associatività, l’esistenza di un elemento di identità e l’esistenza, all’interno del gruppo, dell’inverso di un elemento (che combinato con l’elemento stesso porta all’elemento identità). Sembra complesso ma in realtà facciamo normalmente esperienza di uno di questi gruppi: i numeri interi con l’operazione di addizione.
In matematica esistono diversi gruppi: pensiamo ai gruppi che descrivono le simmetrie di un oggetto quale un quadrato o un altro poligono, oppure i gruppi che nascono a partire da alcune proprietà di certe leggi fisiche. Per esempio le leggi della meccanica classica sono descritte dalle trasformazioni di Galileo che danno luogo al gruppo di Galileo che ci permette di descrivere il mondo fisico classico.
È chiaro quindi come attraverso certi particolari gruppi possiamo descrivere alcuni fenomeni fisici e quindi il «mondo» (Universo) in cui essi vivono.
Spesso è possibile suddividere i gruppi matematici in sotto-gruppi descritti da alcune proprietà particolari e la storia della fisica ci mostra come il gruppo di Galileo sia un sotto-gruppo del gruppo di Lorentz che descrive i fenomeni elettromagnetici formalizzati nelle equazioni di Maxwell e dalla teoria della relatività speciale di Einstein.
Nel passaggio dal gruppo di Galileo a quello di Lorentz ci spostiamo da uno spazio piatto a tre dimensioni (3D), in cui il tempo è assoluto e non è influenzato dal moto, a uno spazio quadri-dimensionale (4D) sempre piatto in cui il tempo non è più assoluto ma diventa una variabile come le usuali coordinate cartesiane.  [A sinistra: Hendric Antoon Lorentz (1853 – 1928)]
[A sinistra: Hendric Antoon Lorentz (1853 – 1928)]
A sua volta il gruppo di Lorentz è un sotto-gruppo di un gruppo più generale come dimostrato da Luigi Fantappié, matematico romano grande amico di Enrico Fermi. Tale gruppo è caratterizzato da due parametri: la velocità della luce c ed il raggio del cronotopo Ru ed il gruppo di Lorentz si ricava da questo ponendo tale raggio infinito. Lo spazio descritto da questo gruppo è uno spazio curvo a 5 dimensioni.
L’idea fondamentale alla base del modello fisico di Serapioni è che l’unica cosa che conta è il movimento (come già puntualizzava Heisenberg) e l’unico movimento possibile sono in realtà rotazioni. Per questo motivo il gruppo di Fantappié e lo spazio 5D a esso associato ben si adattano al modello proposto.
Inoltre l’obbiettivo della teoria è quello di fornire in maniera semplice e geometrica una naturale derivazione dei concetti, per esempio, di massa e carica elettrica che altrimenti devono essere accettati come evidenze dell’esperienza sia per la loro esistenza sia per i valori numerici associati alle particelle/corpi, senza quindi alcuna giustificazione teorica.
Rotazioni, tempo ed eventi
Nello spazio in rotazione in sé introduciamo il concetto di evento definendolo come il tempo che un punto impiega a percorrere una particolare orbita.
Nello spazio a 5D complessivamente avremo un insieme di rotazioni ognuna in un piano ortogonale alle altre e con raggi ΔTi,i=1,…,4 definiti come
![]() in modo che il loro prodotto sia pari al volume dell’ipersfera i-dimensionale di raggio ΔT.
in modo che il loro prodotto sia pari al volume dell’ipersfera i-dimensionale di raggio ΔT.
Tale quantità è posta in relazione al raggio classico dell’elettrone (definito come πλ0) per cui
πΔT4 = RCL = πλ0
A questo punto possiamo introdurre il concetto di tempo. Esso scorre dal passato al futuro passando nel tempo non nullo del presente senza priviligiare alcuna precisa direzione.
Pertanto nello spazio a 5D dove i movimenti sono solo rotazioni dovremo avere un moto di rotazione con un’accelerazione che modifica in ogni istante la propria direzione e quindi sarà un’accelerazione che cambia continuamente.
L’istante viene quindi definito come il tempo che è necessario per modificare la direzione di un’accelerazione. Ma di quante accelerazioni parliamo?
Sfruttando la struttura di spazio a 5D e di gruppo di Fantappiè – generalizzazione del gruppo di Galileo e di Lorentz – possiamo complessivamente definire 5 accelerazioni ortogonali fra di loro. Pertanto oltre al normale spazio a 3D (XYZ) di cui facciamo normale esperienza, in questo modello si ipotizza l’esistenza di un ulteriore spazio normale al primo a due dimensioni estremamente piccole (ST).
È questa la parte sicuramente più originiale del lavoro di Serapioni. Esisterà dunque un rapporto ben preciso e definito tra i tempi di rotazione dell’ente nello spazio a 3D e a 2D.
Nel gruppo di Fantappiè sappiamo che c, velocità della luce, è la velocità con cui ruotano gli enti. Supponiamo un ente in rotazione con una velocità ωXYZ nello spazio 3D lungo una circonferenza di raggio R1. Possiamo scrivere R1=ct1 associando quindi al raggio della circonferenza il tempo impiegato a percorrerla mentre ωXYZ=dθ/dt è associata all’angolo θ spazzato durante il tempo t1.
Otteniamo quindi un’equazione differenziale che porta al rapporto tra il tempo t1 e il tempo fondamentale t0. Ma manca ancora la rotazione nello spazio a 2D. Se immaginiamo quindi che la distanza R1 percorsa sia a sua volta una circonferenza di raggio R2 e percorsa con velocità angolare ωST otteniamo quindi il rapporto
![]() Da questo numero abbiamo già visto è possibile ricavare l’età dell’Universo trovando un accordo estremamente preciso con le misure ottenute da osservazioni del fondo cosmico di microonde da WMAP e Planck.
Da questo numero abbiamo già visto è possibile ricavare l’età dell’Universo trovando un accordo estremamente preciso con le misure ottenute da osservazioni del fondo cosmico di microonde da WMAP e Planck.
Forze di Coriolis
Abbiamo quindi a che fare con accelerazioni centripete necessarie alla descrizione del moto di un ente nello spazio a 5D. Tali accelerazioni saranno inoltre tutte accelerazioni cinematiche dello stesso tipo di quelle legate alla forza di Coriolis.
Anzi nel modello di Serapioni è possibile ricondurre sia la forza elettrostatica che quella gravitazionale a espressioni della forza di Coriolis. In particolare se consideriamo la rotazione di enti che costituisco particelle come elettrone, positrone, …, si constata una variazone di raggio pari a ∆R=±πλ0, che a sua volta produce una variazione di velocità angolare.
Con semplice algebra e meccanica classica si ricava che per questa rotazione la forza di Coriolis si esprime come
![]()
Che coincide con la forza elettrostatica. Da notare il doppio segno derivante dalla variazione del raggio dell’orbita che esprime quindi la natura della carica elettrica legandola al verso di rotazione delle orbite degli enti in rotazione.
In maniera del tutto analoga, considerando la rotazione nello spazio a 2D si ottiene un’espressione analoga della forza di Coriolis che esprime la forza di attrazione gravitazionale.
Vettori Polari
Tutto quanto esposto finora ci permette di introdurre delle quantità che si rivelano di enorme importanza nella trattazione del modello di Universo di Serapioni.
Avendo a che fare con uno spazio a 5D in rotazione in sé, tali quantità sono legate ai rotori che descrivono queste rotazioni. Occorre però fare molta attenzione.
Come è evidente nella nostra esperienza le rotazioni possono avere due versi cioè possono essere sinistrorse oppure destrorse. In uno spazio a 3D la composizione di una rotazione destrorsa con una sinistrorsa di eguale ampiezza danno una risultate che è nulla.
Viceversa in uno spazio a 5D in rotazione in sé, in cui cioè le rotazioni avvengono in piani sempre ortogonali tra di loro, si produrranno rotori non nulli che individuano direzioni sempre ortogonali al comune spazio a 3D.
Queste rotazioni saranno identificate da opportuni «vettori polari» che rappresentano quindi spostamenti di enti. Complessivamente avremo un totale di 9 vettori polari per singolo piano di movimento. Ma essendo 10 i piani diversi propri dello spazio a 5D, avremo un totale di 90 possibili rotazioni ammesse.
È interessante l’emergenza di questo fattore 90 in quanto esso ha forti legami sia con il numero di Dirac che con l’usuale π. Teniamo bene a mente questo fattore 90 perché lo ritroveremo quando proveremo a rendere ragione sia della materia che dell’energia oscura presenti nel nostro Universo.
Grandezze Istantanee e Materia Oscura
Nella teoria di Serapioni ricopre un ruolo molto importante il concetto di «istante» ben distinto dal concetto di «presente» introdotto in precedenza.
L’istante viene definito come un micro-tempo, infinitesimo rispetto al presente, in cui un ente non potrà compiere orbite complete (chiuse) ma solo micro-spostamenti con direzioni lungo i 5 assi dello spazio (XYZ ed ST).
Tali movimenti descrivono nell’istante un insieme di micro-superfici a 2D e dei micro-volumi a 3D tante quante sono le possibili proiezioni di un moto in 5D in due e tre dimensioni.
Nella parte di spazio ST è possibile individuare dei prodotti istantanei tra i micro-spostamenti lungo S e lungo T e l’istante Δt con le dimensioni di una velocità (tempo alla terza potenza).
Viceversa nello spazio a 3D otterremo un analogo prodotto istantaneo con dimensioni di distanza. Complessivamente date le possibile proiezioni avremo 10 vettori velocità e 10 vettori distanza istantanee con cui formeremo un prodotto vettore
VST⋀LXYZ
Che rappresenta 10 rotazioni istantanee differenti (con dimensioni di un tempo alla settima potenza). Da queste rotazioni potremo creare un totale di 5 prodotti indipendenti, creando quindi quantità scalari (con dimensioni di un tempo alla 14esima potenza) che chiameremo masse istantanee od oscure.
 Mappa 3D su larga scala della materia oscura
Mappa 3D su larga scala della materia oscura
Sono istantanee in quanto in ogni istante si creano in un certo punto D dello spazio ma poi spariscono per ri-formarsi in nuovi punti. Pur non lasciando traccia visiva della loro presenza esse eserciteranno comunque una forza di gravità istantanea.
È importante notare a questo punto come il concetto di massa nella teoria proposta nasca sempre da un prodotto vettore come quello appena descritto.
La differenza sostanziale è che per le masse reali e visibili questo prodotto coinvolge velocità e spostamenti reali associati cioè agli enti durante le orbite da loro percorse. Ma la natura è la stessa. Pertanto se ne deduce che il contenuto di materia istantanea (od oscura) risulta 5 volte superiore al contenuto della materia visibile nell’Universo.
Questo risultato ottenuto per via puramente teorica è in ottimo accordo con le misure di materia oscura ottenute attraverso osservazioni del fondo cosmico di microonde.
È questa una fonte indiretta di informazioni sulla materia oscura mentre diversi esperimenti sono in corso di ultimazione per una detection diretta di materia oscura nel tentativo di scoprirne la vera natura.
Energia Oscura
Abbiamo quindi delineato l’esistenza di masse istantanee e verificato come queste siano in grado di rendere ragione delle osservazioni cosmologiche per quanto riguarda l’ammontare di materia oscura presente nell’Universo.
Un altro aspetto che da qualche anno ricopre un interesse da parte della comunità scientifica internazionale è l’osservazione dell’accelerazione dell’Universo.
Queste misure utilizzando supernove lontane (stelle massive alla fine della loro esistenza) che costituiscono delle candele standard (mostrano invariabilmente la stessa curva di luce in quanto le stelle progenitrici coinvolte hanno sempre le medesime caratteristiche) e per cui sembra che al momento della loro esplosione l’Universo si espandesse con una velocità inferiore a quella attuale da cui si deduce una accelerazione nell’espansione.
Tale comportamento non spiegabile utilizzando i «normali» costituenti che compongono l’Universo (materia anche oscura e radiazione) è attribuito a una fantomatica nuova e misteriosa forma di energia detta appunto energia oscura che ha nelle sue caratteristiche una pressione negativa (come se fosse una forza gravitazionale ma repulsiva) responsabile dell’osservata accelerazione.
Tuttavia non abbiamo alcuna teoria fisica che predica un tale comportamento e non possediamo o conosciamo alcun campo fondamentale che mostri queste carattestiche. È pertanto una deduzione indiretta tanto è vero che esistono diversi approcci attualmente in fase di verifica, in grado di spiegare le osservazioni.
All’interno della teoria di Serapioni, l’energia oscura trova una collocazione naturale. Essa è strettamente legata alla struttura fine delle particelle quali quark. Senza entrare nel dettaglio della micro-fisica possiamo comunque vedere subito la stima che ne dà Serapioni.
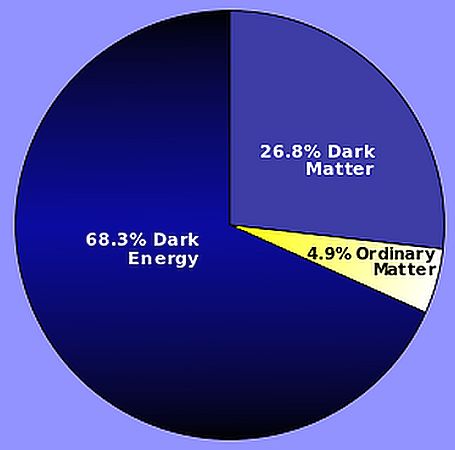
Sappiamo che l’ammontare dell’energia oscura in termini di densità critica si attesta intorno allo 0.683. Quindi quasi il 70% di quello che c’è nell’Universo è energia oscura di cui non sappiamo niente!
Nello spazio a 5D di Serapioni il contributo di energia oscura è calcolabile da quello della materia oscura convertito in energia e pesato per un opportuno contributo dovuto all’entropia. Infatti ricordiamo che tutte le strutture nella teoria proposta, sono strutture ordinate e quindi è necessario «spendere» un po’ di energia per la loro creazione.
Nel caso della struttura fine legata all’energia oscura vedremo che questo fattore vale γ90= 2.6192. L’esponente 90 è, come avevamo accennato in precedenza parlando dei vettori polari, legato al numero totale di rotazioni con velocità differente che un ente può compiere.
Pertanto il contributo di energia oscura dovrà essere pesato per l’entropia e risulta
![]() Occorre a questo punto calcolare anche il contributo dell’energia reale (legato alla massa reale e non immaginaria come nel caso dell’energia oscura). Pertanto
Occorre a questo punto calcolare anche il contributo dell’energia reale (legato alla massa reale e non immaginaria come nel caso dell’energia oscura). Pertanto
![]() L’energia totale dell’Universo sarà quindi la somma di questi due contributi per un totale di
L’energia totale dell’Universo sarà quindi la somma di questi due contributi per un totale di
![]() che porta quindi a un rapporto per l’energia oscura di 0.658 in accordo a meglio del 2% con il valore osservato sperimentalmente.
che porta quindi a un rapporto per l’energia oscura di 0.658 in accordo a meglio del 2% con il valore osservato sperimentalmente.
Davide Maino
(Professore Associato Confermato di Fisica Sperimentale- Università degli Studi di Milano)
© Pubblicato sul n° 62 di Emmeciquadro